About me and why I created this physics website.

Example Mechanics Problems

On this page I give lots of examples of solved mechanics problems. There are over 140 of them and they are fully solved, showing all the steps. They are provided as handwritten PDF files which you can conveniently download. The examples cover mechanics topics at a level typical of physics courses in senior high school, first year college/university, and upper year college/university. This will be very useful when studying for tests and exams. The aim here is to cover many different types of problems, from easy to difficult, to help you study and prepare more effectively. I know that getting access to lots of good problems and their solutions can sometimes be difficult, which is why I created this page, so you have a lot of problems and their solutions all in one convenient place. All these example problems are my own creation, so you won't find an exact copy of them anywhere else. In order to keep them relevant to your courses, I have referenced commonly used physics books to get ideas and inspiration for problems. So there will of course be similarities between them and the problems you will encounter in your classes and physics books.

The example problems are all uniquely numbered for easy reference. The problem statement is given, and then the solution is provided as a PDF file which you can download.

If you want to review the theory behind all these problems, I conveniently cover that on this website, in the kinematics and dynamics pages. If you're studying engineering, there's a problems page on engineering mechanics. Even if you're not studying engineering, it's very useful to study the kinematics problems on that page, if nothing else. They are greatly beneficial in that they give a much deeper coverage of kinematics that also extends into three dimensions. That, in addition to the content on this page, will be of great benefit to you in your overall understanding of mechanics.

To see the example problems click on the category you are interested in:

Kinematics – 1-D problems involving free-fall acceleration (motion along a straight line) – Senior high school and first year college/university
Kinematics – 1-D problems involving constant acceleration (motion along a straight line) – Senior high school and first year college/university
Kinematics – 1-D problems involving average velocity and average speed (motion along a straight line) – Senior high school and first year college/university
Kinematics – 1-D problems involving instantaneous velocity and speed (motion along a straight line) – Senior high school and first year college/university
Kinematics – 1-D problems involving average acceleration and instantaneous acceleration (motion along a straight line) – Senior high school and first year college/university
Kinematics – 2-D and 3-D problems involving position and displacement – Senior high school
Kinematics – 2-D and 3-D problems involving instantaneous velocity, average velocity, and average speed – Senior high school and first year college/university
Kinematics – 2-D and 3-D problems involving instantaneous acceleration and average acceleration – Senior high school and first year college/university
Kinematics – Projectile motion problems – Senior high school and first year college/university
Kinematics – Uniform circular motion – Senior high school and first year college/university
Kinematics – 1-D problems involving relative motion – Senior high school and first year college/university
Kinematics – 2-D problems involving relative motion – Senior high school and first year college/university
Force and motion – Problems involving Newton's laws – Senior high school and first year college/university
Force and motion – Problems involving pulleys – Senior high school and first to upper year college/university
Force and motion – Problems involving friction – Senior high school and first to upper year college/university
Force and motion – Problems involving uniform circular motion – Senior high school and first to upper year college/university
Force and motion – Problems involving rotation, rolling, and torque – First to upper year college/university
Energy – Problems involving work and energy – Senior high school and first to upper year college/university
Energy – Problems involving conservation of energy – Senior high school and first to upper year college/university
Systems – Problems involving systems of particles – Senior high school and first to upper year college/university
Systems – Problems involving momentum – Senior high school and first to upper year college/university
Equilibrium – Problems involving static equilibrium – Senior high school and first to upper year college/university


Kinematics – 1-D problems involving free-fall acceleration (motion along a straight line) – Senior high school and first year college/university

Problem # 1:

A building is under construction, and a construction worker is standing on top of a 130 m high elevator shaft. The worker accidentally drops his hammer down the shaft.

(a) At what speed does the hammer hit the ground?

(b) How much time passes between when the hammer is dropped and when it hits the ground?

(c) What fraction of the total airborne time does the hammer spend in the top 75% of the falling distance?

Download solution

Problem # 2:

A model rocket is launched vertically, and has a constant acceleration of 5.0 m/s² for 8.0 seconds, after which there is no fuel left.

(a) What is the maximum height reached by the rocket?

(b) How much time passes between when the rocket is launched and when it lands?

Download solution

Problem # 3:

An object is dropped from rest, and one second before it lands it is at half its initial drop height.

(a) What is the falling time?

(b) What is the drop height?

Download solution

Problem # 4:

A ball is thrown vertically upward. On its way up it passes point A at a speed v. On its way down it passes point B at a speed that is (3/4)v. Point B is 4.5 m higher than point A.

(a) What is the speed v?

(b) What is the distance between point A and the peak height reached by the ball?

Download solution

Problem # 5:

A drop tower at an amusement park rises at 5 m/s and is 45 m above the ground when one of the riders drops her phone.

(a) How long does it take for the phone to fall to the ground?

(b) At what speed does the phone hit the ground?

Download solution

Problem # 6:

A girl is standing in an elevator moving upward at 5 m/s. She places a launch toy on the floor of the elevator, which then launches a ball straight up at 5.5 m/s relative to the elevator. The girl catches the ball 1.0 seconds later. At the instant the ball is caught, the floor of the elevator is 32 m above the ground.

(a) What is the height of the ball above the ground at the instant it is caught?

(b) What is the height of the elevator floor above the ground at the instant the ball is launched?

Download solution

Problem # 7:

A child is standing in an elevator with glass walls, at a mall. She throws a ball in the air at a vertical upward speed of 4.5 m/s relative to the elevator, and from a height of 1.3 m relative to the elevator floor. At the same time, the elevator is moving upward at 3 m/s, starting from ground level.

(a) From the perspective of the child, what is the maximum height reached by the ball?

(b) From the perspective of someone in the mall (outside the elevator), what is the maximum height reached by the ball?

Download solution

Problem # 8:

A mischievous student drops an egg from the window of his dorm room. The egg falls straight down onto the hood of a car parked below. A few floors below, someone is recording a video on their webcam, which is facing the window. The egg is recorded falling past the window. The person recording the video is a physics student, and she sees an opportunity to solve an interesting physics problem while also determining the height, and consequently the room, that the egg was dropped from. She analyzes the video, and determines that it took the egg 0.14 seconds to fall from the top of the window to the bottom. She then measures the height of the window to be 1.30 meters. From what height, measured from the top of the window, was the egg dropped?

Download solution

Problem # 9:

A game is played by two children, in which one child, at a height of 10 m above the ground, drops a rock with no initial speed. The second child also drops a rock, from a height of 15 m above the ground. The second child drops the rock t_r seconds after the first child drops the rock, with an initial downward speed of 10 m/s. What is the value of t_r so that both rocks hit the ground at the same time?

Download solution

Here are additional free fall problems for you to work on.

Kinematics – 1-D problems involving constant acceleration (motion along a straight line) – Senior high school and first year college/university

Problem # A-1:

A car travelling on a straight road at 25 m/s undergoes constant acceleration until it reaches a speed of 40 m/s. The car then maintains this speed for 6.0 seconds. The brakes are then applied, causing the car to undergo constant deceleration until it once more reaches a speed of 25 m/s. If it takes the car 25 seconds from the time that it starts accelerating to the time that it slows down to 25 m/s, how far does it travel in this time?

Download solution

Problem # A-2:



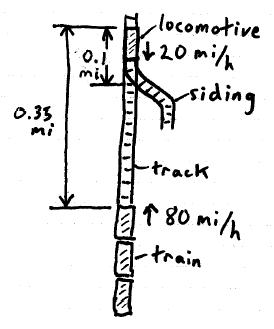
A train is moving at high speed on a straight track, while at the same time a locomotive is moving in the opposite direction on the same track. In order to avoid a collision, the locomotive must move on to the siding before a collision becomes unavoidable. At the same time, the train must decelerate by putting the brakes on. At the instant shown, the front of the train is 0.35 mi from the back of the locomotive, the back of the locomotive is 0.1 mi from the siding entrance, the speed of the train is 80 mi/h, and the maximum speed of the locomotive is 20 mi/h. What is the minimum deceleration of the train?

Download solution

Problem # A-3:



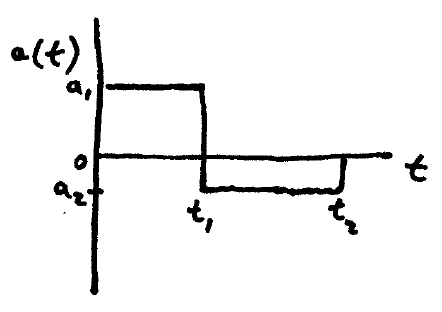
Given the above graph of a(t), sketch the graph of v(t) and d(t).

Download solution

Problem # A-4:

The takeoff speed of a commercial jet is 260 km/h. If the runway is 2.1 km long, what is the minimum constant acceleration of the jet?

Download solution

Problem # A-5:

A truck driving on a paved road is capable of decelerating at a constant value of 5 m/s².

(a) If the truck is initially travelling at 27.4 m/s, how long does it take to come to a complete stop?

(b) How far does the truck travel in this time?

(c) Sketch a graph of distance vs. time and speed vs. time, when the brakes are applied.

Download solution

Problem # A-6:

A distracted driver is cruising at 25 m/s when she suddenly notices a truck directly ahead moving at 15 m/s, in the same direction. At the instant she brakes, the distance between the front of the car and the back of the truck is d. If the car decelerates at 5.0 m/s², and the truck maintains its speed, what is the minimum value of d in order to avoid a collision?

Download solution

Problem # A-7:

A distracted driver is cruising at 25 m/s when he suddenly notices a truck directly ahead moving at 15 m/s, in the same direction. At the instant he brakes, the distance between the front of the car and the back of the truck is 15 m. If the car decelerates at a_c, and the truck maintains its speed, what is the minimum value of a_c in order to avoid a collision?

Download solution

Problem # A-8:

A distracted driver is cruising at 25 m/s when he suddenly notices a truck directly ahead moving at 15 m/s, in the same direction. At the instant he brakes, the distance between the front of the car and the back of the truck is 9 m. The car decelerates at 5 m/s², and one second after the driver of the car applies the brakes, the truck driver notices the car behind and starts accelerating at a_t. What is the minimum value of a_t in order to avoid a collision?

Download solution

Problem # A-9:

A distracted driver is driving on the wrong side of the road, when he notices an oncoming vehicle moving towards him. He quickly applies the brakes, causing his car to decelerate at 4.5 m/s², from an initial speed of 20 m/s. The other driver also applies the brakes, 1.1 seconds later, causing his car to decelerate at 5 m/s², from an initial speed of 23 m/s. At the instant the distracted driver applies the brakes, the front of each car is separated by a distance of 117 m. Is there a collision between the two cars?

Download solution

Kinematics – 1-D problems involving average velocity and average speed (motion along a straight line) – Senior high school and first year college/university

Problem # B-1:

The speed of sound in air is 330 m/s at 0 degrees Celsius. If the average velocity of a jet plane is 2.3 times the speed of sound, how far does it travel in 0.25 seconds?

Download solution

Problem # B-2:

A delivery truck travels up a hill at a constant speed of 50 km/h, in order to deliver a package. After the package is delivered, the truck travels down the same hill at 80 km/h. What is the average speed of the truck for the round trip?

Download solution

Problem # B-3:



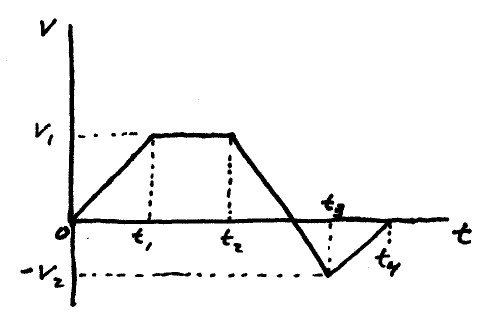
The graph shown above shows velocity vs. time for a particle moving along a straight line. What is the average velocity and average speed for the particle for the entire time the particle is in motion?

Download solution

Problem # B-4:

A particle is moving along the x-axis at a speed defined by s(t) = at + b, where a and b are constants and t is time. If the particle starts moving at time t₁ and stops moving at time t₂, what is the value of a and b so that the average velocity and average speed, between t₁ and t₂, is equal to (1/2)(s(t₁) + s(t₂)).

Download solution

Problem # B-5:

The position of an object moving along the x-axis is given by x = -2t³ + 2t² + 3t − 5, where x is in meters, and t is in seconds.

(a) Find the position of the object at t = 2.0 s, and t = 3.5 s.

(b) What is the displacement of the object between t = 2.0 s, and t = 3.5 s ?

(c) What is the average velocity of the object between t = 2.0 s, and t = 3.5 s ?

(d) What is the average speed of the object between t = 2.0 s, and t = 3.5 s ?

Download solution

Problem # B-6:



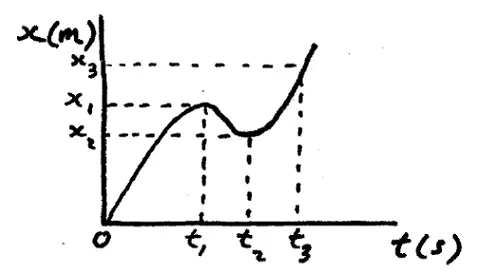
The position of an object moving along the x-axis is shown above, where x is in meters and t is in seconds.

(a) What is the average velocity of the object between 0 and t₃ ?

(b) What is the average speed of the object between 0 and t₃ ?

Download solution

Problem # B-7:

A delivery truck drives 6.5 km along a straight road. The driver then exits the truck, walks 1.5 km to deliver a package at one house, and then continues walking another 2 km to deliver a package to another house. The driver then walks back to the truck. The driving speed of the truck is 70 km/h, and the walking speed of the driver is 5 km/h.

(a) What is the average velocity and average speed of the driver from the start of the drive until the time that the package is delivered to the second house?

(b) What is the average velocity and average speed of the driver from the start of the drive until the time that the driver returns to the truck?

Download solution

Problem # B-8:

An object moves along the positive x-axis at 2 m/s, from point A to point B. It then moves at 3 m/s, from point B to point C. If point C is located halfway between points A and B, what is the average velocity and average speed of the object between points A and C ?

Download solution

Problem # B-9:

An object moves along the positive x-axis, to the right, at speed s₁, from point A to point B. It then moves at speed s₂, from point B to point C. If point C is located to the left of point B, derive an equation relating the average velocity of the object to the average speed of the object, between points A and C.

Download solution

Kinematics – 1-D problems involving instantaneous velocity and speed (motion along a straight line) – Senior high school and first year college/university

Problem # C-1:

The position of a particle is given by x = 4 − 10t + 2t² − 3t³, where t is in seconds and x is in meters.

(a) What is the velocity of the particle at t = 2 s ?

(b) Is the position of the particle increasing or decreasing at t = 2 s ?

(c) What is the speed of the particle at t = 2 s ?

Download solution

Problem # C-2:

A particle's position is given by x = 6 + 4t − 12t² + 6t³, where t is in seconds and x is in meters.

(a) At what time is the velocity of the particle equal to -1.5 m/s ?

(b) At what time is the speed of the particle equal to 1.5 m/s ?

(c) What is the minimum velocity and minimum speed of the particle?

Download solution

Kinematics – 1-D problems involving average acceleration and instantaneous acceleration (motion along a straight line) – Senior high school and first year college/university

Problem # D-1:

A particle's position is given by x = 2 + 4t − 5t² + 9t³, where t is in seconds and x is in meters.

(a) What is the average acceleraton of the particle between t = 1 s and t = 2 s ?

(b) What is the acceleraton of the particle at t = 3 s ?

Download solution

Problem # D-2:

A particle is moving towards the right at 21 m/s, at a time of 3.1 s, and is moving towards the left at 18 m/s, at a time of 6.4 s. What is the average acceleration of the particle from 3.1 s to 6.4 s ?

Download solution

Problem # D-3:



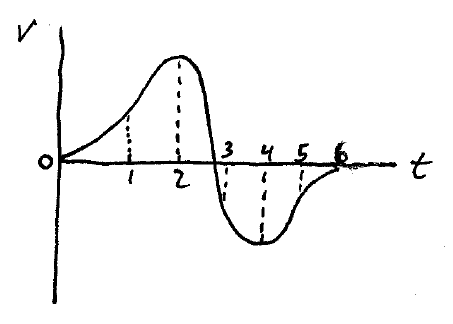
A particle moves in a straight line, as represented by the above graph of velocity vs. time. Sketch a graph representing the acceleration of this particle.

Download solution

Problem # D-4:



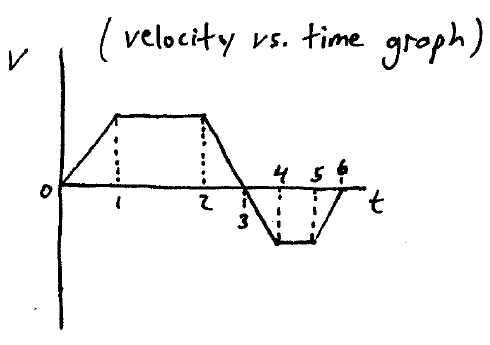
A particle moves in a straight line, as represented by the above graph. Sketch a graph representing the acceleration of this particle.

Download solution

Problem # D-5:

A particle moves in a straight line at 12 m/s, and some time later it is moving at −21 m/s. If the average acceleration of the particle is −2.5 m/s², how much time has passed between the initial and final velocity?

Download solution

Kinematics – 2-D and 3-D problems involving position and displacement – Senior high school

Problem # E-1:

A particle has the following coordinates: x = −4.0 m, y = 7.0 m, and z = 2.0 m.

(a) Find the position vector in unit-vector notation.

(b) What is the magnitude of this vector?

(c) Sketch the vector on a right-handed coordinate system.

Download solution

Problem # E-2:

A particle has the following coordinates initially: x = 4.5 m, y = −3.5 m. Some time later the coordinates are: x = −1.5 m, y = 2.0 m.

(a) Find the displacement vector of the particle.

(b) Sketch the initial, final, and displacement vector of the particle.

Download solution

Problem # E-3:

A particle has the following coordinates initially: x = 1.0 m, y = −3.0 m, z = 8.0 m. Some time later the coordinates are: x = 3.0 m, y = −5.0 m, z = 4.0 m. What is the displacement vector of the particle?

Download solution

Kinematics – 2-D and 3-D problems involving instantaneous velocity, average velocity, and average speed – Senior high school and first year college/university

Problem # F-1:

A plane flies 350 mi east from airport A to airport B in 50 min, and then flies 500 mi south from airport B to airport C in 1.8 h.

(a) Determine the displacement vector, for the total trip.

(b) Determine the average velocity vector, for the total trip.

(c) Determine the average speed, for the total trip.

Download solution

Problem # F-2:

In 4.2 h, a weather balloon drifts 10.2 km west, 18.7 km south, and 3.1 km upward.

(a) Determine the magnitude of the balloon's average velocity, and the angle that this vector makes with the horizontal.

(b) Determine the average speed of the balloon.

Download solution

Problem # F-3:

The position of a particle is given by r = 4i − 2t²j + 8t³k, with r in meters, and t in seconds.

(a) What is the instantaneous velocity of the particle at t = 2.0 s ?

(b) What is the magnitude of the instantaneous velocity at t = 2.0 s ?

Download solution

Kinematics – 2-D and 3-D problems involving instantaneous acceleration and average acceleration – Senior high school and first year college/university

Problem # G-1:

A particle has initial velocity v = 3.0i − 4.0j + 8.0k, and 5.0 s later it has final velocity v = 2.0i − 1.0j + 3.0k. Units are in m/s.

(a) What is the average acceleration over the 5.0 s interval?

(b) What is the magnitude of the average acceleration, and show the orientation of the average acceleration.

Download solution

Problem # G-2:

A particle is initially located at the origin and has an initial velocity of v = 3.0i + 2.0j − 1.0k, in meters per second. It experiences a constant acceleration of a = −1.0i − 1.5j, in meters per second squared.

(a) What is the velocity of the particle when its y-coordinate is a maximum?

(b) Where is the particle located at this instant?

Download solution

Problem # G-3:

The position of a particle is given by r = t²i + (t³ − 5t)j − 3.0tk, in meters. What is the instantaneous acceleration of the particle? What is the orientation of the instantaneous acceleration at t = 1.0 s ?

Download solution

Kinematics – Projectile motion problems – Senior high school and first year college/university

Problem # H-1:



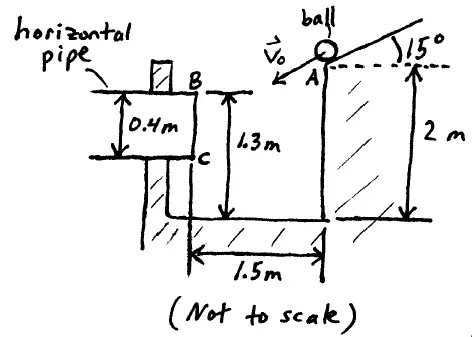
A ball rolls down a ramp that is inclined at 15° with the horizontal. At the edge of the ramp (point A), the velocity of the ball is v₀. Determine the range of values of v₀ so that the ball enters the horizontal pipe shown.

Download solution

Problem # H-2:



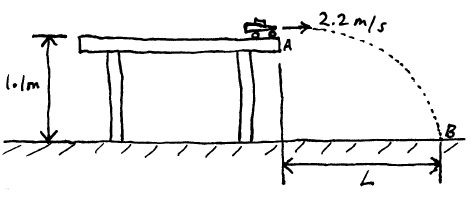
A remote controlled toy car is driven off the edge of a table, at point A, at a speed of 2.2 m/s. It lands at point B. If the table is 1.1 m high, what is the horizontal distance, L, between point A and point B?

Download solution

Problem # H-3:



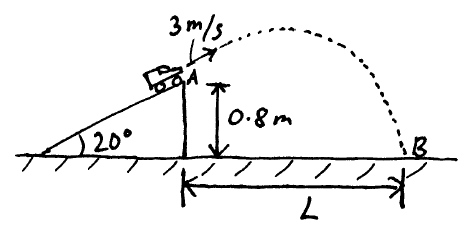
A remote controlled toy car is driven off the edge of a ramp, at point A, at a speed of 3 m/s. It lands at point B. If the edge of the ramp is at a height of 0.8 m, and it is inclined at 20° with the horizontal, what is the horizontal distance, L, between point A and point B?

Download solution

Problem # H-4:



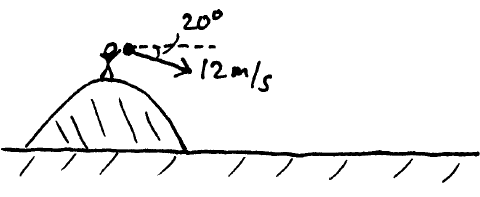
A person standing at the top of a hill throws a rock with an initial velocity of 12 m/s at an angle of 20° below the horizontal.

(a) Calculate the horizontal displacement of the rock 1.5 s later.

(b) Calculate the vertical displacement of the rock 1.5 s later.

Download solution

Problem # H-5:



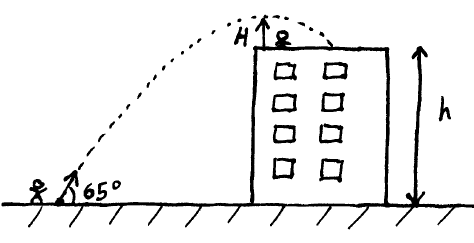
In order to calculate the height, h, of a building, a physics student launches a ball at an initial speed of 30 m/s at an angle of 65° above the horizontal. Another physics student is standing on the roof of the building, and determines that the ball lands on the roof of the building 3.5 s after it is launched.

(a) What is the height, h, of the building?

(b) What is the peak height, H, reached by the ball, relative to the student on the roof?

Download solution

Problem # H-6:



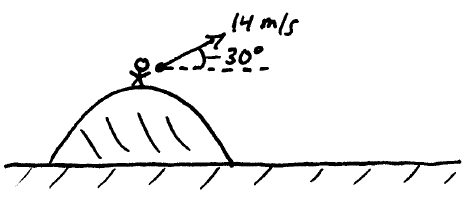
A person standing at the top of a hill throws a rock with an initial velocity of 14 m/s at an angle of 30° above the horizontal.

(a) Calculate the horizontal displacement of the rock 1.7 s later.

(b) Calculate the vertical displacement of the rock 1.7 s later.

(c) How long does it take the rock to fall 3.5 m below its initial launch height?

Download solution

Problem # H-7:

A ball is launched from the ground into the air. At a height of 7.3 m, the velocity of the ball is observed to be v = 8.2i + 5.7j in meters per second.

(a) What is the maximum height reached by the ball?

(b) What will be the total horizontal distance traveled by the ball?

(c) At the instant just before the ball hits the ground, what is the magnitude and direction of its velocity?

Download solution

Problem # H-8:



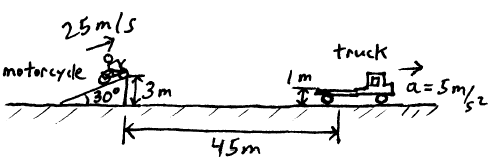
A stuntman rides his motorcycle at 25 m/s off a ramp that is inclined at 30°. He intends to land on the back of a truck. The driver of the truck must wait T seconds after the motorcycle launches off the ramp, before accelerating, from rest, at 5 m/s², so that the motorcycle lands on the back of the truck. The edge of the ramp is 3 m high, the back of the truck is 1 m high, and the back of the truck is 45 m from the edge of the ramp, initially. What is the value of T ?

Download solution

Problem # H-9:



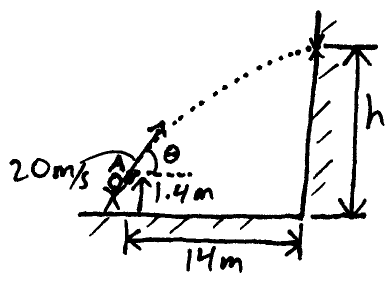
A baseball player throws a ball at an initial speed of 20 m/s, from point A, which is 1.4 m above the ground and 14 m from a wall. What is the launch angle θ so that the height h, which is the distance from the ground to the point of impact on the wall, is a maximum?

Download solution

Problem # H-10:



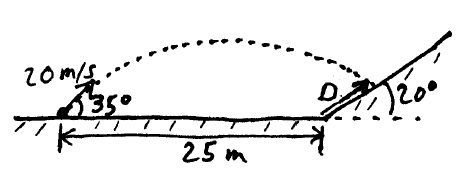
A ball is launched at ground level at a speed of 20 m/s, at an angle of 35° above the horizontal. A hill is located 25 m from the launch point, where it has an inclination of 20°. How far up the hill, D, does the ball land?

Download solution

Problem # H-11:



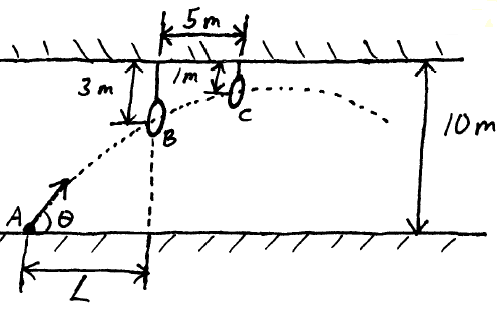
In a competition held in a high school gym, the goal is to launch a ball from floor level so that it passes through two rings suspended from the ceiling, as shown. One of the competitors is a physics student who calculates the value of L and θ based on a launch speed of 20 m/s. What are these two values?

Download solution

Here are additional projectile motion problems for you to work on.

Kinematics – Uniform circular motion – Senior high school and first year college/university

Problem # I-1:

A sprinter is running around the bend of a track with radius of 30 m, at a speed of 11 m/s. What is the acceleration of the sprinter and in what direction does the acceleration a point?

Download solution

Problem # I-2:

A charged particle moves in a circular path in a magnetic field, with a radial acceleration of 2.5 × 10¹⁴ m/s². If the circular path has a radius of 14 cm, what is its speed?

Download solution

Problem # I-3:

A fan rotates at 1000 revolutions per minute. The tip of the blades have a radius of 0.20 m.

(a) What is the distance traveled by the tip of a blade during one full revolution?

(b) What is the speed of a blade tip?

(c) What is the acceleration of a blade tip?

Download solution

Problem # I-4:

A high speed train goes around a curve at a speed of 250 km/h. What is the smallest radius of curvature of the track so that the maximum acceleration experienced by the passengers is 0.05g ?

Download solution

Problem # I-5:

A high speed train goes around a curve with a radius of 1.5 km. What is the maximum speed of the train so that the maximum acceleration experienced by the passengers is 0.05g ?

Download solution

Problem # I-6:



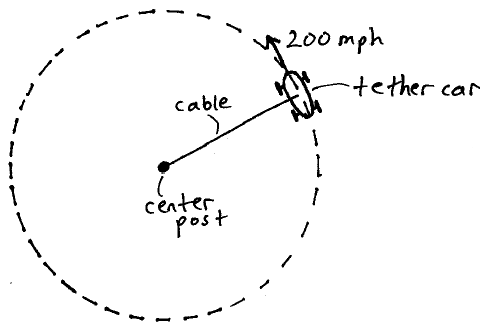
A tether car is going around a track at a speed of 200 mph. To prevent the car from going off the track it is tethered to a center post with a cable. The diameter of the track is 21.3 m, and the wheel diameter of the car is 5 cm.

(a) What is the acceleration of the car?

(b) How fast do the car wheels rotate, in revolutions per minute?

(c) Looking at the car from above, how fast does it go around the track, in revolutions per minute?

Download solution

Kinematics – 1-D problems involving relative motion – Senior high school and first year college/university

Problem # J-1:

A boat is traveling in a river in the upstream direction, at 15 km/h with respect to the water of the river. The water in the river is flowing at 7 km/h with respect to the ground.

(a) What is the velocity of the boat with respect to ground?

(b) A person on the boat walks from the front of the boat to the back of the boat at 5 km/h with respect to the boat. What is the person's velocity with respect to the ground?

Download solution

Problem # J-2:

A person walks up an escalator that has stopped, in 100 seconds. When the escalator is moving, it takes the person 75 seconds to be carried up when they are standing on it. If the escalator is 20 m long, how long would it take that same person to walk up the moving escalator?

Download solution

Problem # J-3:

A cameraman is standing on the back of a pickup truck filming a scene for a movie. He videotapes a car traveling directly ahead of him moving at 45 mi/h faster than the truck. Suddenly, the car slows down, stops, and begins moving in the opposite direction at 60 mi/h, as measured by someone on the ground. If the pickup truck is moving at 35 mi/h, and the change in the car's velocity took 2.5 seconds, what was the acceleration of the car from the perspective of (a) the cameraman, and (b) the person on the ground?

Download solution

Kinematics – 2-D problems involving relative motion – Senior high school and first year college/university

Problem # K-1:



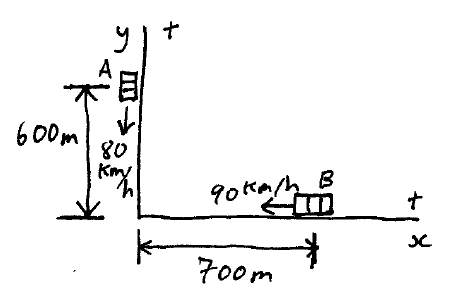
Two cars, A and B, are approaching an intersection as shown. Car A is 600 m from the intersection and is moving at 80 km/h. Car B is 700 m from the intersection and is moving at 90 km/h.

(a) In unit vector notation, what is the velocity of car A with respect to car B?

(b) How does the direction of the velocity found in (a) compare to the line of sight between the two cars?

(c) How does the answer to (a) and (b) change as the cars move closer to the intersection?

Download solution

Problem # K-2:

A train travels in the north direction at 25 m/s relative to the ground. At the same time it is raining. An observer on the ground sees that the raindrops make an angle of 18° with the vertical. A passenger on the train sees the raindrops fall in a perfectly vertical direction. What is the speed of the raindrops relative to the ground?

Download solution

Problem # K-3:

The pilot of a plane intends to fly directly east in the presence of a wind, a distance of 950 km. The plane has an airspeed of 630 km/h, and the pilot calculates that the plane must fly with a heading of 15° south of east. If the plane arrives at the destination 1.8 hours later, what was the velocity vector of the wind?

Download solution

Problem # K-4:

A 350 m wide river flows in the east direction at 2.5 m/s. A boat with a speed of 9.5 m/s relative to the water sets a course that is pointed in a direction 25° west of north.

(a) What is the velocity of the boat relative to the Earth?

(b) How long does it take the boat to cross the river, starting from the south bank?

Download solution

Problem # K-5:

A river flows in the east direction at 3.5 m/s. A boat with a speed of 8.5 m/s relative to the water sets a course that is pointed in a direction 30° north of east. Once the boat is in motion, one of the passengers walks from the left side of the boat directly to the right side of the boat at a speed of 1.5 m/s relative to the boat. What is the velocity of the passenger relative to the ground?

Download solution

Here are additional relative velocity problems for you to work on.

Force and motion – Problems involving Newton's laws – Senior high school and first year college/university

Problem # L-1:



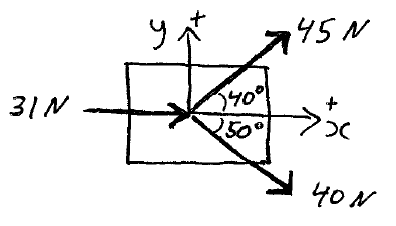
Three forces are applied to a 2 kg slab, as shown. What is the slab's acceleration in unit-vector notation, and expressed as a magnitude and direction?

Download solution

Problem # L-2:



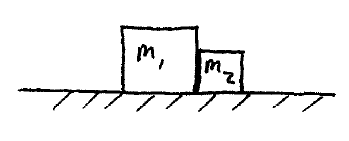
Suppose a force of 10.5 N is acting on the mass m₁, towards the right, and then the same force acts on mass m₂, towards the left. Assume both masses are on a frictionless surface, with m₁ = 3 kg and m₂ = 1.2 kg. For each situation, what is the contact force between the two masses?

Download solution

Problem # L-3:

A block of mass 2 kg is sliding along a flat frictionless surface at a velocity of 5 m/s. A force of 6 N is applied opposite the direction of motion of the block, and the block slows down to a velocity of 2 m/s. What is the travel distance of the block over the time period that the force is applied?

Download solution

Problem # L-4:



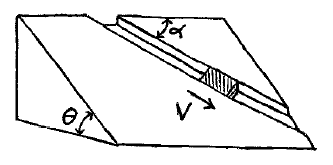
A block of mass m slides at constant velocity v along a groove cut into an inclined plane, as shown. What is the magnitude and direction of the force exerted on the block by the inclined plane?

Download solution

Problem # L-5:



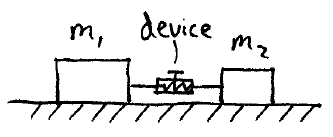
Two masses, m₁ and m₂, are sitting on a flat frictionless surface. They are joined together by two ropes which are connected to a device containing a spring under tension. A pin is pulled which releases the spring causing it to contract with a force of 6 N. If m₁ = 3 kg and m₂ = 1.4 kg, what is the acceleration of each mass?

Download solution

Problem # L-6:

At an amusement park, a drop tower falls with an acceleration of 8.1 m/s². What is the upward force exerted on a 63 kg rider?

Download solution

Problem # L-7:

A helicopter is accelerating upward at 1.5 m/s². What is the upward force exerted on a 72 kg passenger?

Download solution

Problem # L-8:



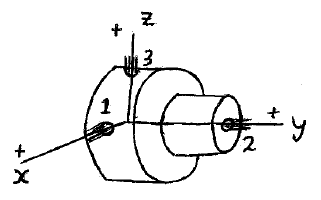
A space capsule simultaneously fires three of its thrusters, denoted by 1, 2, 3. If the thrusters fire for 9.5 s, and F₁ = 50 N, F₂ = 60 N, and F₃ = 65 N, what is the velocity of the capsule after 9.5 s ? The capsule is initially moving along the positive y-direction at 30 m/s, and its mass is 120 kg.

Download solution

Problem # L-9:

A sphere of mass m is suspended from the roof of a car with a cord of length 25 cm. As the car accelerates, the cord makes an angle of 35° with the vertical. What is the acceleration of the car?

Download solution

Force and motion – Problems involving pulleys – Senior high school and first to upper year college/university

Problem # M-1:



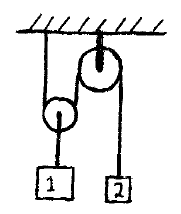
In the pulley system shown, block 1 has a mass of 80 kg and block 2 has a mass of 30 kg. If the system is released from rest, what is the speed of block 2 after 1.5 seconds? Neglect the mass of the pulleys and rope.

Download solution

Problem # M-2:



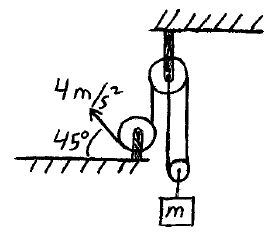
In the pulley system shown, block m has a mass of 120 kg. If one end of the rope is being pulled at an acceleration of 4 m/s², what is the rope tension? Neglect the mass of the pulleys and rope.

Download solution

Problem # M-3:



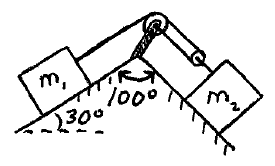
In the pulley system shown, the two blocks are released from rest. The sliding surfaces are frictionless, and the mass of the rope and pulleys is negligible. Determine the acceleration of each block and the tension in the rope. Note that m₁ = 50 kg and m₂ = 150 kg.

Download solution

Problem # M-4:



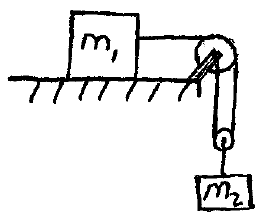
In the pulley system shown, the two blocks are released from rest. The sliding surface is frictionless, and the mass of the rope and pulleys is negligible. Determine the acceleration of each block and the tension in the rope. Note that m₁ = 10 kg and m₂ = 20 kg.

Download solution

Problem # M-5:



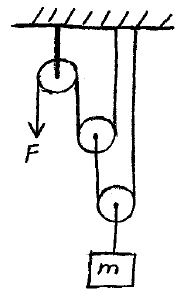
In the pulley system shown, block m has a mass of 16 kg. What is the constant force F that must be applied to the rope so that the block has an upward acceleration of 2 m/s². Neglect the mass of the pulleys and rope.

Download solution

Problem # M-6:



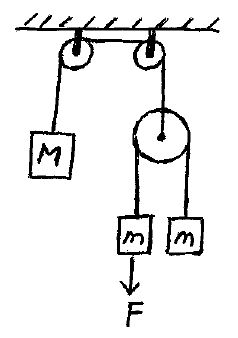
Block M has a mass of 40 kg and both blocks m have a mass of 20 kg each. The mass of the pulleys and ropes are negligible. All blocks start from rest and the left block m moves a distance of 2 m in 1.5 s. Determine the tension in the ropes and the magnitude of the force F.

Download solution

Problem # M-7:



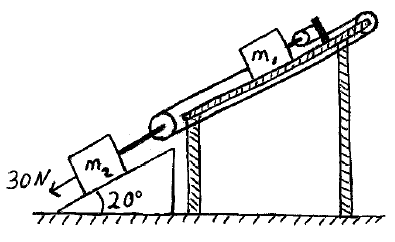
In the pulley system shown, two blocks are released from rest. The sliding surfaces are frictionless, and the mass of the pulleys and rope are negligible. After 1.3 s, what is the velocity of each block? Note that m₁ = 10 kg and m₂ = 30 kg.

Download solution

Force and motion – Problems involving friction – Senior high school and first to upper year college/university

Problem # N-1:



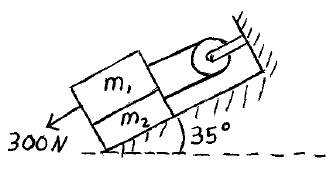
In the system shown, the coefficient of static friction between all contact surfaces is 0.15, and the coefficient of kinetic friction between all contact surfaces is 0.10. Determine the acceleration of the blocks and the tension in the rope. Note that m₁ = 20 kg and m₂ = 10 kg.

Download solution

Problem # N-2:



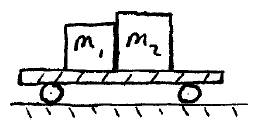
Two blocks are sitting on a wheeled platform which is initially stationary. The coefficient of kinetic friction between the left block and the platform is 0.15, and the coefficient of kinetic friction between the right block and the platform is 0.10. The platform is given a sudden push to the right causing slippage between it and the blocks. Determine the acceleration of the blocks and the force between them. Note that m₁ = 15 kg and m₂ = 20 kg.

Download solution

Problem # N-3:



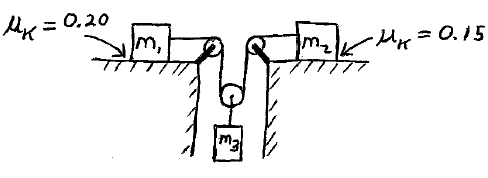
In the pulley system shown, m₁ = 6 kg, m₂ = 13 kg, and m₃ = 10 kg. Determine the acceleration of each block and the tension in the rope.

Download solution

Problem # N-4:



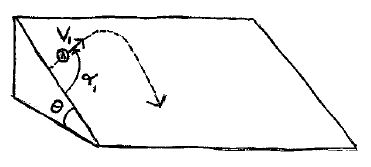
A disk is launched at an initial speed v₁ at an angle α₁ as shown, on an inclined plane. If the coefficient of kinetic friction is equal to tan θ, what is the final speed of the disk assuming the incline is large enough so that the disk slides for a long time?

Download solution

Problem # N-5:



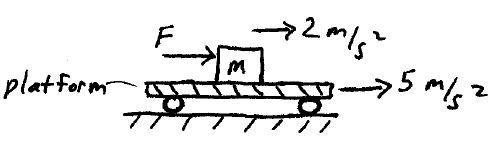
A platform is accelerating to the right at 5 m/s², and a mass m is on top of the platform and has an acceleration of 2 m/s² relative to the platform. If m = 6 kg and the coefficient of kinetic friction between the mass and platform is 0.25, what is the force F applied to the mass? If the relative acceleration of the mass is in the opposite direction, what is the force F ?

Download solution

Problem # N-6:



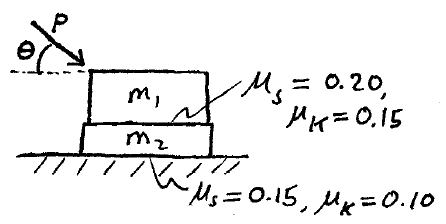
A force P is applied to a mass m₁ which makes an angle θ with the horizontal. Find an expression for P(θ) for the case where (a) the mass m₁ and mass m₂ move as a single unit, and (b) there is relative slipping between mass m₁ and mass m₂.

Download solution

Problem # N-7:



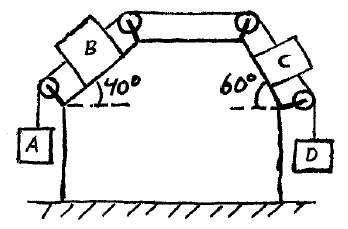
In the pulley system shown, m_A = 10 kg, m_B = 20 kg, m_C = 8 kg, and m_D = 5 kg. If the coefficient of kinetic friction between the blocks and the sliding surface is 0.15, what is the acceleration of block A and what is the tension in the different rope segments?

Download solution

Problem # N-8:



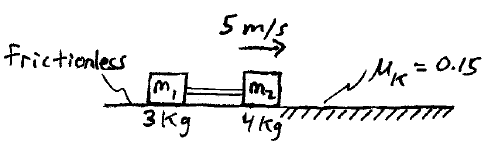
Two masses, m₁ and m₂, are sliding on a frictionless surface at a speed of 5 m/s. The front mass, m₂, encounters a rough patch and experiences friction, and then the mass connected behind it, m₁, encounters the rough patch a short time later, and it too experiences friction. If the rod connecting the two masses has negligible mass, how far do both masses slide once the front mass encounters the rough patch? The rod is 2 m long. Ignore the dimension of m₁ and m₂.

Download solution

Problem # N-9:



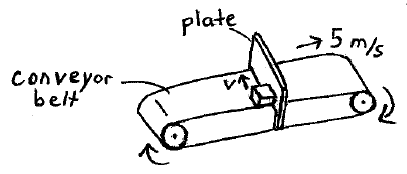
A block of mass 2 kg is sitting on top of a conveyor belt moving at 5 m/s. The block is prevented from moving with the belt with a plate, as shown. As a result, the belt slides underneath the block with a speed of 5 m/s relative to the block. The coefficient of kinetic friction between the block and belt is 0.20, and there is no friction between the block and the plate. Suppose that someone were to push the block in the tranverse direction at a speed v, as shown. What is the force applied by the person?

Download solution

Here are additional friction problems and pulley problems for you to work on.

Force and motion – Problems involving uniform circular motion – Senior high school and first to upper year college/university

Problem # O-1:



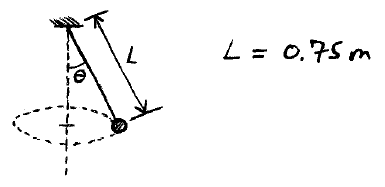
A 3 kg ball is attached to a string of length L and revolves in a horizontal circle, as shown. If the speed of the ball is constant and equal to 2.5 m/s, what is the angle θ and the tension in the string?

Download solution

Problem # O-2:



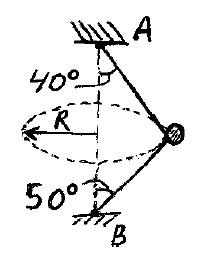
A 3 kg ball is going around in a horizontal circle of radius R = 2.1 m. A single string passes through a ring attached to the ball and is supported at both ends A and B, as shown. Determine the speed of the ball, which is constant.

Download solution

Problem # O-3:



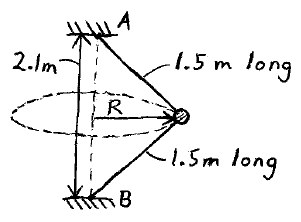
A 3 kg ball is going around in a horizontal circle of radius R. The ball is connected to two strings which are supoorted at A and B, as shown. If the tension in the upper string is twice the tension in the lower string, what is the speed of the ball?

Download solution

Problem # O-4:



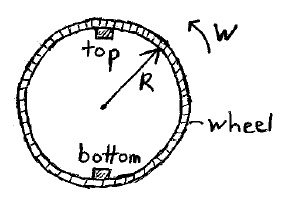
A block is sitting on the inside of a wheel rim, which has radius R = 1.4 m. The wheel is oriented vertically and is rotating at an angular velocity w. The coefficient of static friction between wheel and block is 0.20.

(a) What is the minimum value of w so that the block doesn't slide on the rim?

(b) What is the minimum value of w so that the block doesn't fall off the rim?

(c) For each of the values of w in (a) and (b), what is the contact force between the block and rim at the top and bottom position, as shown? Use mass of block = 2.5 kg.

Download solution

Problem # O-5:



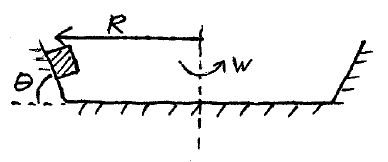
A person riding a Gravitron at an amusement park can be modelled as a block, as shown. It is given that θ = 70°, R = 6 m, and the coefficient of static friction between the person and the wall of the Gravitron is 0.25. What is the range of angular velocities, w, of the Gravitron so that the person does not slide up or down the wall?

Download solution

Problem # O-6:



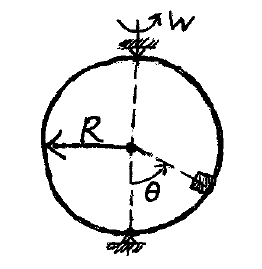
A hollow sphere with a block of mass 0.500 kg inside of it is rotating with an angular velocity, w, of 8.5 rad/s. If the inside radius of the sphere is R = 0.7 m, determine the values for θ if (a) there is no friction between the block and sphere and the block stays in contact with the sphere wall and does not slide on the sphere wall, (b) the coefficient of static friction between the block and sphere is 0.25 and the block stays in contact with the sphere wall and does not slide on the sphere wall.

Download solution

Problem # O-7:



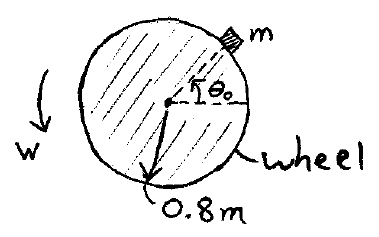
A block of mass m is placed on a wheel oriented vertically, rotating with an angular velocity of w = 2 rad/s. If the block is placed initially with no slippage on the wheel, at what angle θ₀ can the block be placed so that the block stays on the wheel, without losing contact or slipping, for as long as possible? The coefficient of static friction is 0.30.

Download solution

Force and motion – Problems involving rotation, rolling, and torque – First to upper year college/university

Problem # P-1:



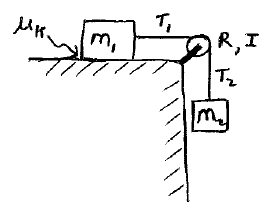
In the pulley system shown, the two blocks have a mass m₁ and m₂, the pulley radius is R, the rotational inertia of the pulley is I, and the coefficient of kinetic friction between the block and surface is μ_k. Determine (a) the angular acceleration of the pulley, (b) the acceleration of the blocks, and (c) the tensions in the upper and lower sections of the rope. Assume the system is in motion.

Download solution

Problem # P-2:



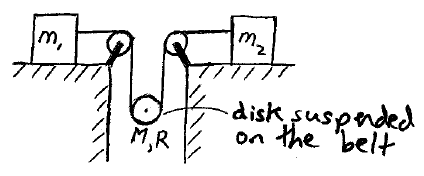
In the pulley system shown, m₁ = 2 kg, m₂ = 3 kg, M = 5 kg, R = 5 cm, and the coefficient of kinetic friction between the blocks and surface is 0.15. The mass of the belt and pulleys is negligible. Determine the angular acceleration of the disk and the acceleration of its center of mass.

Download solution

Problem # P-3:



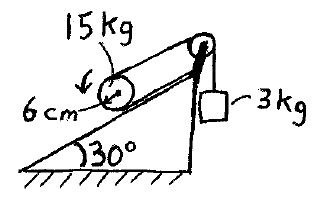
In the pulley system shown, determine the acceleration of the block. The mass of the belt and pulley is negligible.

Download solution

Problem # P-4:



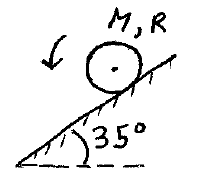
A cylinder is rolling down an incline, as shown. What is the minimum coefficient of static friction between the cylinder and surface so that the cylinder rolls without slipping? Suppose the coefficient of kinetic friction between the cylinder and surface is 0.10. What is the angular acceleration of the cylinder and what is the acceleration of its center of mass? Compare this to the no-slipping case. Note that M = 10 kg and R = 6 cm.

Download solution

Problem # P-5:



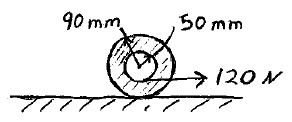
A cord is wound around the inner drum of a spool and pulled with a horizontal force of 120 N. The mass of the spool is 40 kg, and its radius of gyration is 60 mm. If μ_s = 0.15 and μ_k = 0.10, determine the angular acceleration of the spool and the acceleration of its center of mass.

Download solution

Problem # P-6:



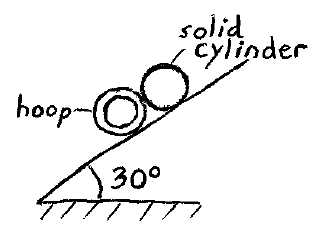
A hoop and solid cylinder are initially in contact on an incline, as shown. The mass of each is 50 kg and the radius of each is 30 cm. Is it possible for the hoop and cylinder to both remain stationary, and in contact, on the incline? If the coefficient of kinetic friction between the hoop and cylinder is 0.10, what is the angular acceleration of each, and what is the acceleration of the center of mass of each? How many rotations does the hoop and cylinder complete after each has rolled a distance of 1 meter?

Download solution

Here are additional problems for you to work on related to force and motion:

Force problems
Inclined plane problems
Torque problems

Here are examples of force and motion analysis in three-dimensions:

Bowling
Euler's disk
Gyroscopes

Energy – Problems involving work and energy – Senior high school and first to upper year college/university

Problem # Q-1:



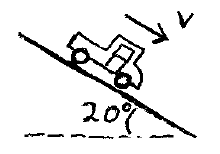
A truck is going down a hill that has an inclination of 20°. If the truck is travelling at constant speed v, what is the power dissipated by the brakes? If the truck then travels up the hill at constant speed v, what is the power produced by the engine? The mass of the truck is 6,000 kg, and the resistance force acting on the truck is 1,200 N.

Download solution

Problem # Q-2:



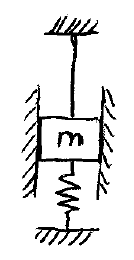
A mass m is supported from above by a rope, and supported from below by a spring. The rope has a tension of 15 N, the spring stiffness is 900 N/m, and m = 4 kg. If the rope is cut, determine the maximum displacement of the mass, and determine the maximum velocity of the mass.

Download solution

Problem # Q-3:



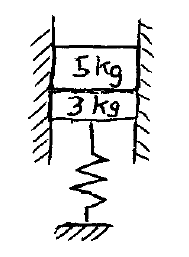
A 5 kg mass is slowly placed on a 3 kg mass that is initially at rest while supported by a spring underneath. If the spring stiffness is 250 N/m, what is the maximum compression amount of the spring, and what is the maximum velocity of the masses?

Download solution

Problem # Q-4:



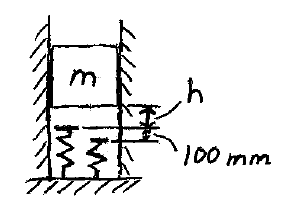
A block of mass m is released from rest and falls a distance h before contacting the spring on the left, as shown, and then falls further down a distance of 100 mm before contacting a second spring on the right, as shown. The stiffness of the spring on the left is 1000 N/m, and the stiffness of the spring on the right is 2000 N/m. If the maximum compression of the spring on the left is 200 mm, determine the value of h. The mass m = 9 kg.

Download solution

Problem # Q-5:



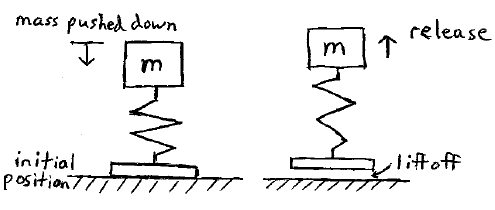
A mass m is attached to a spring, and pushed downward so that the spring is compressed 30 cm. The mass is then released and the spring-mass system lifts off from the ground, as shown. The maximum liftoff height is 0.60 m. If the mass m = 15 kg, what would be the maximum liftoff height on the moon, given that the acceleration due to gravity, on the moon, is one-sixth that on Earth? Ignore the mass of the spring and bottom support for spring.

Download solution

Problem # Q-6:



A block on a flat horizontal surface has a force F with magnitude 120 N applied to it. The coefficient of kinetic friction between the block and surface is 0.15. What is the velocity of the block when it has moved a distance of 2.5 meters? The mass of the block is m = 3 kg, and θ = 30°. The block is initially at rest.

Download solution

Problem # Q-7:



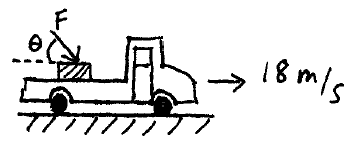
A block on the back of a truck, traveling at a constant velocity of 18 m/s, has a force F with magnitude 120 N applied to it. The coefficient of kinetic friction between the block and truck surface is 0.15. What is the velocity of the block when it has moved a distance of 2.5 meters, relative to the truck? Calculate the answer from the point of view of an observer on the ground, and on the truck. The mass of the block is m = 3 kg, and θ = 30°. The block is initially at rest on the truck.

Download solution

Energy – Problems involving conservation of energy – Senior high school and first to upper year college/university

Problem # R-1:



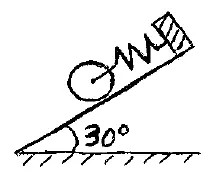
A cylinder is attached to a spring, while on an incline, as shown. The cylinder is released from rest when the spring is neither stretched nor compressed. The mass of the cylinder is 25 kg, its radius is 8 cm, and the spring stiffness is 500 N/m. What is the maximum and minimum speed of the cylinder, and the corresponding stretch amount of the spring? Assume the cylinder rolls without slipping.

Download solution

Problem # R-2:



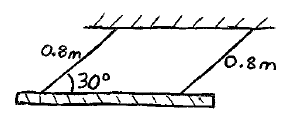
A board of mass 16 kg is suspended from two cables, each of length 0.8 m, and each making an angle of 30° with the horizontal. While in this position, the board is released from rest. What is the velocity of the board when it is at its lowest position? Ignore the mass of the cables.

Download solution

Problem # R-3:



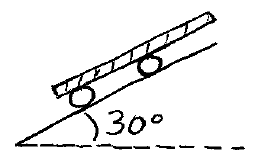
A board is supported by two cylinders on an incline, as shown. The mass of the board is 12 kg, the mass of each cylinder is 5 kg and their radius is 5 cm. If the system is released from rest and there is no slipping anywhere, what is the velocity of the board after it has moved a distance of 1.2 meters? Assume the board stays in contact with the cylinders.

Download solution

Problem # R-4:



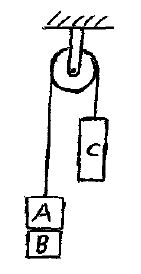
In the pulley system shown, m_A = 4 kg, m_B = 5 kg, and m_C = 11 kg. The masses A and B are glued to each other. The system is released from rest and when mass C has fallen 0.4 m, mass B detaches from mass A due to poor quality glue. Determine the velocity of mass C when it has fallen 0.7 m. Ignore the mass of the rope and pulley.

Download solution

Problem # R-5:



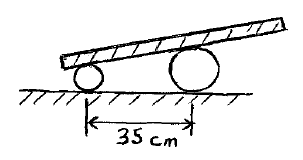
A board is supported by two cylinders on a horizontal surface, as shown. The mass of the board is 13 kg, the mass and radius of the smaller cylinder is 5 kg and 5 cm, and the mass and radius of the larger cylinder is 10 kg and 7 cm. If the system is released from rest and there is no slipping anywhere, what is the velocity of the board after the cylinders have moved a distance of 30 cm ? Assume the board stays in contact with the cylinders.

Download solution

Here are additional problems for you to work on related to energy:

Energy problems
Kinetic energy problems

Systems – Problems involving systems of particles – Senior high school and first to upper year college/university

Problem # S-1:



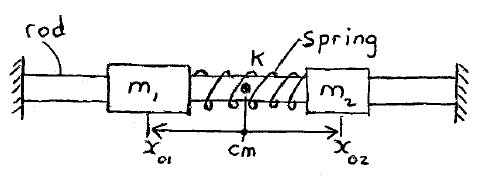
Two masses, m₁ and m₂, can slide without friction on a horizontal rod. A spring of stiffness k is connected between the two masses. At the instant shown, the masses m₁ and m₂ are located a distance x₀₁ and x₀₂ from the center of mass (cm) of the system, respectively. At this instant, the spring is stretched by an amount ΔL, and the velocity of the two masses is zero. Find expressions for the distances x₁ and x₂ over time, after the system is released. Note that the system is defined here as the masses m₁ and m₂, and the spring. The mass of the spring is small relative to m₁ and m₂, so it can be ignored.

Download solution

Problem # S-2:



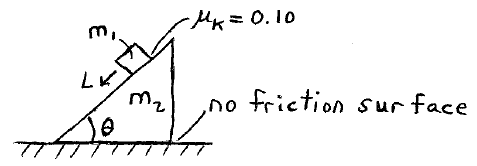
In the system shown, a mass m₁ slides a distance L down an incline of mass m₂. How far does the incline slide along the surface, and in what direction?

Download solution

Problem # S-3:



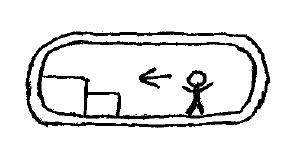
An underwater capsule is stationary relative to the sea floor. The capsule has a mass of 2,200 kg. An 80 kg passenger in the capsule stands up, causing his center of mass to rise 40 cm relative to the capsule. The passenger then walks to the left a distance of 1.8 m relative to the capsule. What is the displacement of the capsule as a result of the movement of the passenger?

Download solution

Problem # S-4:

A cannon of mass 1,400 kg fires a ball of mass 60 kg in the horizontal direction with a velocity of 53 m/s relative to the cannon. What is the velocity of the cannon and ball relative to the Earth?

Download solution

Problem # S-5:

A water container of initial mass 120 kg is being lifted at constant velocity, v = 0.8 m/s. The container has a leak and is losing 1.2 kg of water per second. Find an expression for the force required to lift the container, over time. What if the container was instead accelerating upward at 0.4 m/s² ?

Download solution

Problem # S-6:



Two masses, m₁ and m₂, are pushed against a spring of stiffness k. The spring is initially compressed by an amount ΔL, and then the masses are simultaneously released. What is the final velocity of the two masses?

Download solution

Problem # S-7:



A chute is dumping sand onto a conveyor belt at the rate of 5 kg/s. The belt has a linear speed of 1.3 m/s. What is the power produced by the motor running the conveyor belt?

Download solution

Problem # S-8:

A 2-stage rocket has an initial mass of 1,250 kg. At the end of its first stage, the rocket has a mass of 500 kg. At this point, the lower section of the rocket separates, and the top section of the rocket begins firing. The lower section of the rocket has a mass of 200 kg. At the end of the second stage, the mass of the rocket (consisting only of the top section) is 140 kg. For both stages, the rocket consumes fuel at the rate of 2.4 kg/s. The speed of the exhaust gases relative to the rocket engine is 2,800 m/s. What is the speed increase of the rocket at the end of the second stage, and what is the thrust produced by the rocket? The rocket is in deep space where there is negligible gravitational force acting on it.

Download solution

Systems – Problems involving momentum – Senior high school and first to upper year college/university

Problem # T-1:



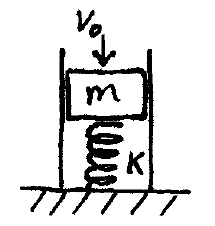
A mass m falling downward contacts a spring of stiffness k, with a velocity v₀. What is the duration of the impact (the time that the spring and mass are in contact)? What is the impulse during the impact? What is the average force acting on the mass during the impact?

Download solution

Problem # T-2:

A golfer hits a golf ball, giving it an initial velocity of 60 m/s with a launch angle of 40° above the horizontal. The club and ball are in contact for 1.9 ms, and the mass of the ball is 45 g. Determine, (a) the impulse acting on the ball and the club, (b) the average force acting on the ball, and (c) the work done on the ball.

Download solution

Problem # T-3:

A child throws a ball having a mass of 150 g against a wall, with a speed of 6 m/s. The ball rebounds with a 40% reduction in its kinetic energy. Determine, (a) the speed of the ball immediately after rebounding, (b) the impulse acting on the ball and wall, and (c) the average force exerted on the ball if the contact time between ball and wall was 8.3 ms.

Download solution

Problem # T-4:

A space capsule separates into two parts, as a result of detonating the explosive bolts holding the two parts together. The magnitude of impulse acting on each part is 350 N·s. If the masses of the two parts are 1,300 kg and 1,900 kg, what is the relative speed of separation of the two parts?

Download solution

Problem # T-5:

As a result of an impact, an average force of 120 N acts on an object of mass 1.5 kg, in the x-direction, causing its velocity in the x-direction to reach 4.2 m/s. At the same time, an average force of 90 N acts on the object in the y-direction. If the initial velocity of the object in the x and y direction is 1.5 m/s and 0.6 m/s, respectively, what is the final speed of the object in the y-direction?

Download solution

Problem # T-6:



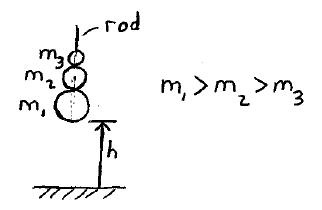
A toy consists of 3 rubber balls of mass m₁, m₂, and m₃, which have a thin rod threaded through them, allowing the balls to slide freely along the rod. The toy is dropped from a height h above the ground. If all collisions are elastic, what is the height reached by the ball with mass m₃ ?

Download solution

Problem # T-7:

A 3.5 ton weight falls a distance of 1.8 m, and then impacts a 0.6 ton pile. As a result of this completely inelastic collision, the pile is driven 3 cm into the ground. Find the average force exerted on the pile by the ground?

Download solution

Problem # T-8:

A 40 ton train car collides with another train car that is stationary. The two cars couple together as a result, and 32% of the initial kinetic energy is lost during the collision. Determine the mass of the second train car.

Download solution

Problem # T-9:



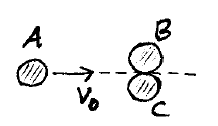
Ball A is moving towards two balls, B and C, as shown, at a velocity of 5 m/s. Friction is negligible and the collision is elastic. If the balls are all identical, determine the velocities of all 3 balls after the collision.

Download solution

Problem # T-10:



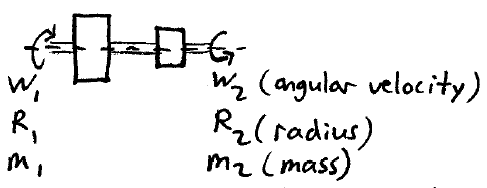
Two rotating cylinders are brought into contact, as shown. Due to friction between the cylinders, they eventually reach the same angular velocity. What is this angular velocity? Note that the cylinders are initially rotating in opposite directions.

Download solution

Problem # T-11:



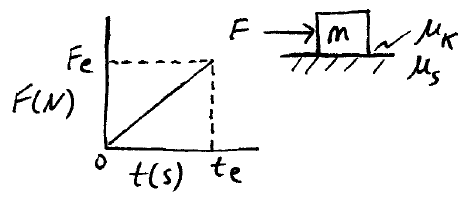
A block is initially at rest on a horizontal surface, and a force F is applied to it. Given the force vs. time graph, as shown, determine the velocity of the block at time t_e. Assume F_e > μ_smg.

Download solution

Here are additional momentum problems for you to work on.

Equilibrium – Problems involving static equilibrium – Senior high school and first to upper year college/university

Problem # U-1:



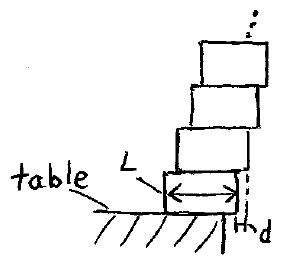
Identical blocks of length L are placed on top of each other. Each block extends a distance d beyond the one underneath, and the bottom block also extends a distance d beyond the edge of the table. What is the maximum number of blocks that can be stacked?

Download solution

Problem # U-2:



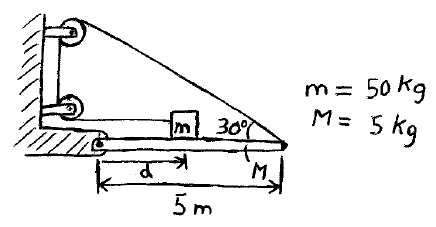
In the system shown, the coefficient of static friction between the mass m and the board M is 0.20. Determine the value of d so that the system is in equilibrium.

Download solution

Problem # U-3:



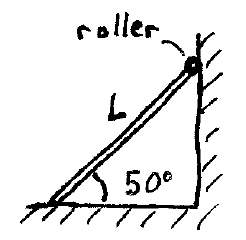
A uniform board of length L = 20 ft is leaning against a wall, as shown. The top end of the board has a roller on it. If the board has a weight of 70 lb, what is the minimum coefficient of static friction between board and ground?

Download solution

Problem # U-4:



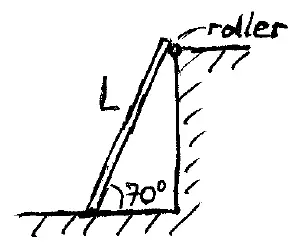
A uniform board of length L = 20 ft is leaning against a roller, as shown. If the board has a weight of 70 lb, what is the minimum coefficient of static friction between board and ground?

Download solution

Problem # U-5:



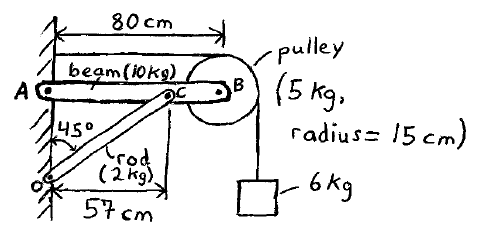
In the system shown, determine the forces acting on the rod at point O, and the beam at point A.

Download solution

Here are additional statics problems for you to work on.

Here are additional mechanics problems for you to work on which cover different topics, so they are a good review.



Return to Real World Physics Problems home page