About me and why I created this physics website.

Projectile Motion Problems

On this page I put together a collection of projectile motion problems to help you understand projectile motion better. The required equations and background reading to solve these problems is given on the projectile motion page.

I also provide hints and numerical answers for these problems.


Refer to the figure below (along with sign convention shown), for problems 1-7. Use g = 9.8 m/s².



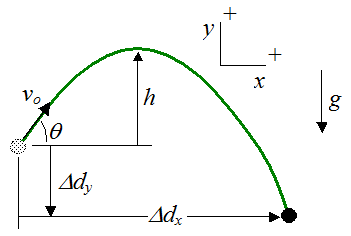
For problems 1-6 and 8, ignore air resistance in your calculations.


Problem # 1

For Δd_y = 0 and for any given v_o find θ so that the range (Δd_x) is maximum.

Hint and answer


Problem # 2

Find the maximum height (h) and range for v_o = 10 m/s, θ = 30°, and Δd_y = -10 m. What is the flight time?

Hint and answer


Problem # 3

Find the maximum height and range for v_o = 10 m/s, θ = 30°, and Δd_y = 1 m. The displacement Δd_y corresponds to the stage of the projectile flight where it is moving downward. What is the flight time?

Hint and answer


Problem # 4

Find Δd_y for v_o = 10 m/s, θ = 30°, and Δd_x = 15 m. What is the flight time?

Hint and answer


Problem # 5

Find the maximum height and range for v_o = 10 m/s, and θ = 90°.

Hint and answer


Problem # 6

Find the maximum height and range for v_o = 10 m/s, θ = 0, and Δd_y = -5 m.

Hint and answer


Problem # 7

Find the maximum height and range for v_o = 10 m/s, θ = 30°, and Δd_y = -10 m. Account for air resistance, with drag coefficient equal to 0.47, projected frontal area equal to 0.01 m², density of air equal to 1.2 kg/m³, and mass of projectile equal to 0.1 kg. Compare this to the answer in problem 2.

Hint and answer


Problem # 8



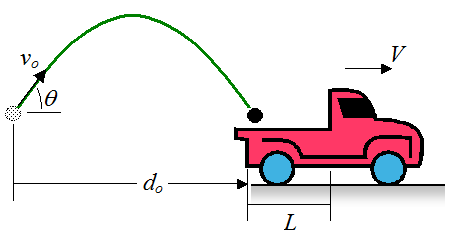
A ball is kicked at an angle θ = 45°. It is intended that the ball lands in the back of a moving truck which has a trunk of length L = 2.5 m. If the initial horizontal distance from the back of the truck to the ball, at the instant of the kick, is d_o = 5 m, and the truck moves directly away from the ball at velocity V = 9 m/s (as shown), what is the maximum and minimum velocity v_o so that the ball lands in the trunk. Assume that the initial height of the ball is equal to the height of the ball at the instant it begins to enter the trunk.

Hint and answer


The hints and answers for these projectile motion problems will be given next.

Hints And Numerical Answers For Projectile Motion Problems


Hint and answer for Problem # 1

Referring to the projectile motion page, set v_x = v_ocosθ and v_1y = v_osinθ. Obtain an explicit expression for time t based on the quantities v_1y and Δd_y, and find θ so that Δd_x is maximum.

Answer: θ = 45°


Hint and answer for Problem # 2

Refer to the projectile motion page. To find maximum height set v_1y = v_osinθ. We know that at maximum height there is zero vertical velocity (v_2y = 0). There is a specific equation on the projectile motion page which you can use to solve for the maximum height when v_2y = 0. To find the range you first need to find the total time t the projectile is airborne, and then you can use this time to find the range Δd_x = v_xt where v_x = v_ocosθ.

Answer: h = 1.276 m, Δd_x = 17.556 m, t = 2.027 s


Hint and answer for Problem # 3

This problem is similar to problem 2 so the hint for it applies here as well. Note that there are two solutions for time t which correspond to Δd_y = 1 m. You must choose the largest time t corresponding to the stage of the flight where the projectile is moving downward.

Answer: h = 1.276 m, Δd_x = 6.472 m, t = 0.747 s


Hint and answer for Problem # 4

Given known Δd_x = (v_ocosθ)t, with v_o and θ known, find t and then use this t to find Δd_y using the equation for vertical displacement (Δd_y) on the projectile motion page.

Answer: Δd_y = -6.04 m, t = 1.732 s


Hint and answer for Problem # 5

This projectile motion problem involves strictly vertical projectile motion, which means there is no horizontal velocity component to consider.

Answer: h = 5.102 m, Δd_x = 0


Hint and answer for Problem # 6

This projectile motion problem involves initially horizontal projectile motion, which means there is no initial vertical velocity component to consider.

Answer: h = 0, Δd_x = 10.102 m


Hint and answer for Problem # 7

You need to solve this with numerical methods which accounts for the effects of air resistance. I created a projectile motion simulator to solve problems like this.

Answer: h = 1.175 m, Δd_x = 14.22 m


Hint and answer for Problem # 8

When the ball begins to enter the trunk, the horizontal distance Δd_x traveled by the ball is given by Δd_x = (v_ocosθ)t, which is also equal to the distance d_o+Vt for minimum v_o and d_o+L+Vt for maximum v_o, where t is the total time. To determine the total time t set Δd_y = 0, and solve for t. You can then solve for minimum v_o and maximum v_o.

Answer: Minimum v_o = 15.824 m/s, maximum v_o = 17.041 m/s


Projectile motion problems like the ones given above are a good way to test understanding. To see an interesting real-world application of projectile motion go to The Physics Of Volleyball.

Also, see the problem, Maximum shot put distance.

---

Bonus Problems Related to Projectile Motion

1. Will a penny dropped from the top of the Empire State Building kill a person or penetrate the ground? (from urban myth)

2. Can a football fly farther if it is filled with helium?

3. Can a bullet fired straight up in the air kill someone on the way back down?

4. If a person jumps out of an airplane with the last parachute, can another person jump out later and catch the person?

5. Does a 4,000 foot fall take 90 seconds?

6. Will a car dropped from 4,000 feet fall faster than a speeding car?

I created a physics analysis for these six problems, in PDF format. It's available through this link.



Return to Kinematics page


Return to Real World Physics Problems home page