About me and why I created this physics website.

Mechanics Problems

On this page I put together a collection of mechanics problems to help you understand mechanics better. The required equations and background reading to solve these problems is given on the kinematics page and the dynamics page. Mechanics is a broad area of physics, and these problems are taken from a broad range of experiences that arise naturally in day-to-day life.

The solutions are provided as handwritten PDF files.


Problem # 1

During a bench press, does the amount of work, or power, required depend on the rate at which the weight is lifted?

Solution


Problem # 2

A car has a mass of 1700 kg, a drag coefficient of 0.35, a rolling resistance coefficient of 0.01, a frontal area of 2 m², and a horsepower of 150. What is the minimum time required for the car to go from 0 to 60 mph? What is the minimum time if the car has 300 horsepower, with all else the same? Use a density of air of 1.2 kg/m³, and g = 9.8 m/s². Assume the car is on a perfectly flat surface and assume that the wheels don't slip.

Solution


Problem # 3

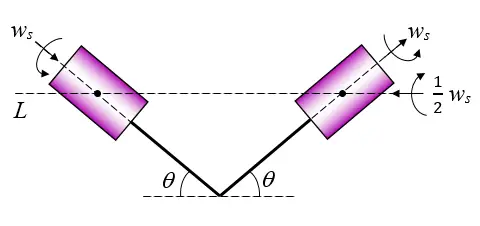
The cat righting reflex allows a cat to flip 180° from an upside down position, upon falling, so that it can land on its feet. By twisting a certain way, the cat can do this while maintaining zero angular momentum. To help understand how this is possible, consider the following physical system shown below, representing the cat. Relative to the shafts, the (identical) cylinders spin at an angular velocity w_s, while the shafts spin in the opposite sense with angular velocity (1/2)w_s, with respect to ground. Find the angle θ so that this is possible. The mass of each cylinder is m, the radius of each cylinder is a, and the length of each cylinder is 3a. Ignore the mass of the shafts.

Solution




Problem # 4

In a game of pool, calculate the trajectory of the cue ball after it strikes the object ball. The coefficient of kinetic friction between cue ball and table is μ_k. Assume the pool table is perfectly flat.

Solution


Problem # 5

An inflated basketball has a mass of 0.624 kg and a radius of 0.119 m. Find the effective gravity acting on the basketball, given a density of air of 1.2 kg/m³, and g = 9.8 m/s².

Solution


Problem # 6

Does the length of a skateboard affect the jumping distance over a ramp?

Solution


Problem # 7

A heavy payload of mass 5000 kg needs to be pulled along a flat surface that has rollers on it. The speed of the payload as it is pulled is not to exceed 20 m/s. The payload is to increase in speed gradually as it is pulled, starting from rest. The pulling distance is 20 m. The plan is to use an engine or motor to rotate a heavy flywheel up to a certain rotational speed, and then disengage the engine/motor and use the rotating flywheel to pull the payload. Doing this avoids having to use a very powerful engine/motor, and instead allows the use of a much less powerful engine/motor to slowly add energy to an inertial system which will then have enough power to pull the payload. Design a flywheel system that can pull the payload as desired.

Solution


Problem # 8

If someone can vertically jump a height h on earth, with g = 9.8 m/s², how high can they jump on another planet with a different value of g? Let H be the vertical lift distance (before takeoff) of the center of mass of the jumper during the propelling phase of the jump.

Solution


Problem # 9

A bullet is fired out of a gun with a velocity of 300 m/s, with respect to ground. If the bullet has a mass of 0.06 kg and the gun has a mass of 1.5 kg, what percentage of the total kinetic energy (of the bullet and gun) does the bullet have?

Solution


Problem # 10

The fully extended arm length of a shot putter is b, and his shoulder height is h_s. What angle θ should the (fully extended) arm of the shot putter make with the ground in order to maximize the distance of the shot? Assume the ground is horizontal.

It is given that the launch velocity V_o of the shot is given by:

V_o² = 2(E(θ)/m − gbsinθ), where g = 9.8 m/s², m is the mass of the shot put, and

E(θ) = 106.18m(2 + cosθ)/3

Use b = 0.8 m, and h_s = 1.66 m.

Solution


Problem # 11

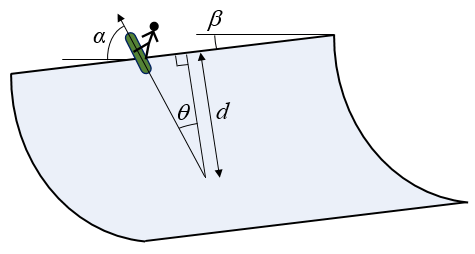
A snowboarding half-pipe has an angle of inclination (pitch) of β = 18° and a wall height of d = 7 m. What is the optimal takeoff angle θ for a snowboarder to reach maximum height, maximum airborne time, and maximum distance along the half-pipe? Note that the angle α is measured from the horizontal and is useful in your calculations.

Solution





Return to Physics Questions page


Return to Real World Physics Problems home page