About me and why I created this physics website.

Pulley Problems

On this page I put together a collection of pulley problems to help you understand pulley systems better. The required equations and background reading to solve these problems are given on the friction page, the equilibrium page, and Newton's second law page.

Problem # 1

A block of mass m is pulled, via pulley, at constant velocity along a surface inclined at angle θ. The coefficient of kinetic friction is μ_k, between block and surface. Determine the pulling force F. Answer: mgcosθμ_k+mgsinθ




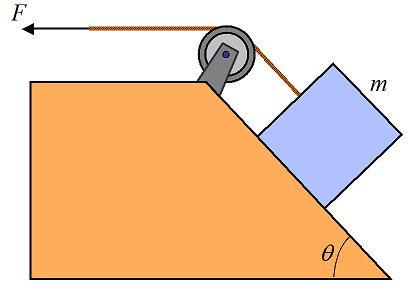
Problem # 2

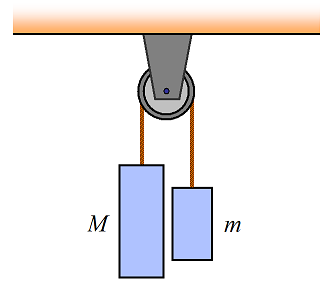
Two blocks of mass m and M are hanging off a single pulley, as shown. Determine the acceleration of the blocks. Ignore the mass of the pulley.

Hint and answer




Problem # 3

Two blocks of mass m and M are connected via pulley with a configuration as shown. The coefficient of static friction is μ_s, between block and surface. What is the maximum mass m so that no sliding occurs? Answer: maximum m = Mμ_s




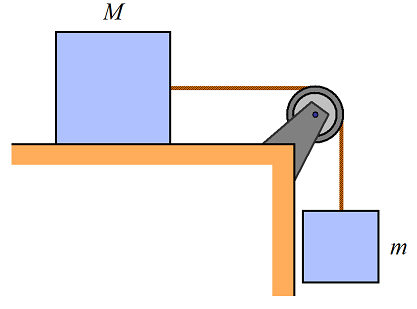
Problem # 4

Two blocks of mass m and M are connected via pulley with a configuration as shown. The coefficient of static friction is μ_s, between block and surface. What is the minimum and maximum mass M so that no sliding occurs?

Hint and answer




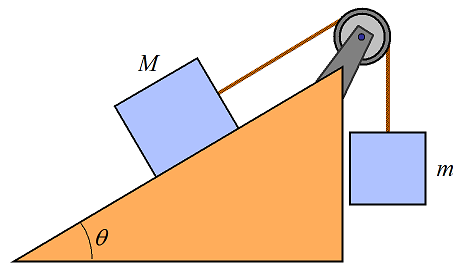
Problem # 5

Two blocks of mass m and M are connected via pulley with a configuration as shown. The coefficient of static friction is μ_s, between blocks and surface. What is the maximum mass m so that no sliding occurs? Answer: Maximum m = Mμ_s/(sinθ−cosθμ_s)




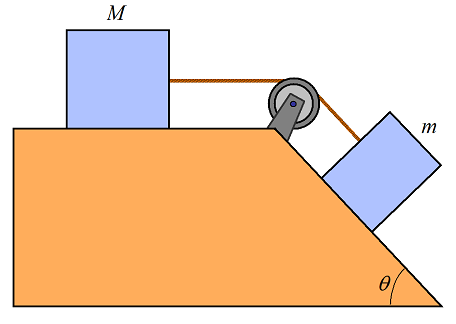
Problem # 6

Two blocks of mass m and M are connected via pulley with a configuration as shown. The coefficient of static friction between the left block and the surface is μ_s1, and the coefficient of static friction between the right block and the surface is μ_s2. Formulate a mathematical inequality for the condition that no sliding occurs. There may be more than one inequality.

Hint and answer




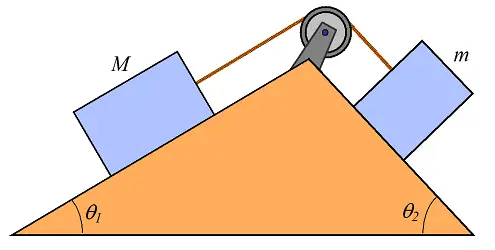
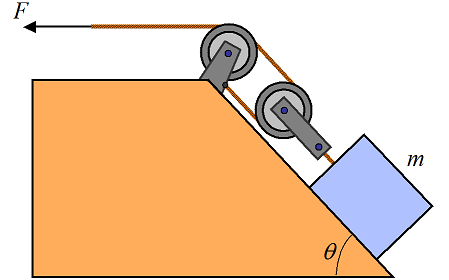
Problem # 7

A block of mass m is pulled, via two pulleys as shown, at constant velocity along a surface inclined at angle θ. The coefficient of kinetic friction is μ_k, between block and surface. Determine the pulling force F. Ignore the mass of the pulleys.

Hint and answer




Problem # 8

A block of mass m is lifted at constant velocity, via two pulleys as shown. Determine the pulling force F. Ignore the mass of the pulleys.

Hint and answer




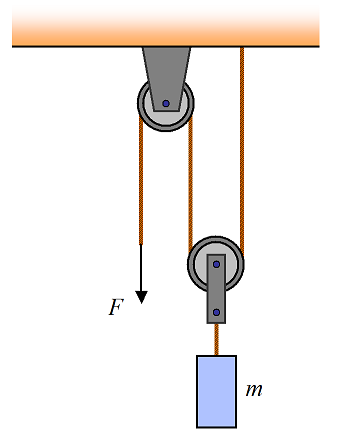
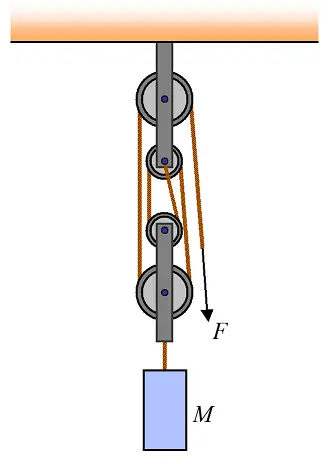
Problem # 9

A block of mass M is lifted at constant velocity, via an arrangement of pulleys as shown. Determine the pulling force F. Ignore the mass of the pulleys.

Hint and answer




The hints and answers for these pulley problems will be given next.

Hints And Answers For Pulley Problems


Hint and answer for Problem # 2

This is called the Atwood machine and is commonly used for demonstration in physics classes.

Apply Newton's second law to the block on the left. We have Mg−T = Ma (taking the downward direction as positive). Apply Newton's second law to the block on the right. We have mg−T = -ma (the acceleration of the two blocks have opposite signs, since one moves up and the other moves down). Combine these two equations and we can find an expression for the acceleration of the blocks.

Answer: a = (M−m)g/(M+m)


Hint and answer for Problem # 4

For the maximum mass M, the block is on the verge of sliding down the incline. This means that Mgsinθ−T−Mgcosθμ_s = 0, where T is the tension in the rope. Since T = mg, we can calculate the maximum M from the previous equation.

For the minimum mass M, the block is on the verge of sliding up the incline. This means that Mgsinθ−T+Mgcosθμ_s = 0, where T = mg. We can calculate the minimum M from the previous equation.

Answer: Minimum M = m/(sinθ+cosθμ_s), Maximum M = m/(sinθ−cosθμ_s)


Hint and answer for Problem # 6

This is a challenging problem! It took me a while to figure this one out!

At some angle θ₁ > θ_max1 block M will slide down on its own if there is no rope attached. Similarly, at some angle θ₂ > θ_max2 block m will slide down on its own if there is no rope attached.

It is known that θ_max1 = atan(μ_s1) and θ_max2 = atan(μ_s2).

If θ₁ ≤ θ_max1 and θ₂ ≤ θ_max2 then no sliding occurs. There are three more cases to consider.

Case 1:

θ₁ > θ_max1 and θ₂ ≤ θ_max2.

Apply the equilibrium equation to block M in which it is on the brink of sliding down. We have: Mgsinθ₁−Mgcosθ₁μ_s1−T_min1 = 0, where T_min1 corresponds to the minimum rope tension preventing block M from sliding down. (Note that the system naturally "settles" such that the rope tension T required to stop the block from sliding down is the minimum possible amount). For T < T_min1 the block slides down. From this equation we get T_min1 = Mgsinθ₁−Mgcosθ₁μ_s1. Call this equation (1).

There is no need to consider block M sliding up since it is an impossibility for θ₂ ≤ θ_max2 (which means block m cannot slide down which means it cannot pull block M up).

T_min1 must be provided by the block m and must not exceed the maximum rope tension which can be resisted by block m and not be pulled up the incline. This maximum rope tension can be determined from the following equilibrium equation applied to block m: mgsinθ₂+mgcosθ₂μ_s2−T_max2 = 0, from which T_max2 = mgsinθ₂+mgcosθ₂μ_s2. Call this equation (2).

For no sliding T_min1 ≤ T_max2. Therefore, from equation (1) and (2) we have the final inequality for this case:

Msinθ₁−Mcosθ₁μ_s1 ≤ msinθ₂+mcosθ₂μ_s2

Case 2:

θ₁ ≤ θ_max1 and θ₂ > θ_max2.

This is the same as case 1, by symmetry. Hence, the final inequality for this case is:

msinθ₂−mcosθ₂μ_s2 ≤ Msinθ₁+Mcosθ₁μ_s1

Case 3:

θ₁ > θ_max1 and θ₂ > θ_max2.

The blocks will slide together in one direction or the other. To determine the direction we must first calculate the net force pulling down on each block along their respective inclines, as a result of gravity. We do this as follows:

For block M, F_net1 = Mgsinθ₁−Mgcosθ₁μ_s1. And F_net1 > 0 since θ₁ > θ_max1.

For block m, F_net2 = mgsinθ₂−mgcosθ₂μ_s2. And F_net2 > 0 since θ₂ > θ_max2.

We now have three sub-cases to consider. The final inequalities for this case will be given within these three sub-cases, as follows.

     Case 3A:

If F_net1 = F_net2 the blocks will not slide.

     Case 3B:

If F_net1 > F_net2, then F_net1 ≤ mgsinθ₂+mgcosθ₂μ_s2 for no sliding. Note that F_net1 is equal to the rope tension, and this rope tension is the minimum required to prevent block M from sliding down the incline.

Hence, for no sliding: Msinθ₁−Mcosθ₁μ_s1 ≤ msinθ₂+mcosθ₂μ_s2

     Case 3C:

If F_net2 > F_net1, then F_net2 ≤ Mgsinθ₁+Mgcosθ₁μ_s1 for no sliding. Note that F_net2 is equal to the rope tension, and this rope tension is the minimum required to prevent block m from sliding down the incline.

Hence, for no sliding: msinθ₂−mcosθ₂μ_s2 ≤ Msinθ₁+Mcosθ₁μ_s1

We are done!


Hint and answer for Problem # 7

Apply the condition of static equilibrium to the block. We have 2F−mgsinθ−mgcosθμ_k = 0. The term 2F comes from a force analysis in which we see that there are two segments of rope pulling equally on the block. We then solve this equation for F.

Answer: F = (1/2)mg(sinθ+μ_kcosθ)


Hint and answer for Problem # 8

Apply the condition of static equilibrium to the block. We have 2F−mg = 0. The term 2F comes from a force analysis in which we see that there are two segments of rope pulling equally on the block. We then solve this equation for F.

Answer: F = mg/2


Hint and answer for Problem # 9

Upon close inspection we see that the bottom two pulleys are held up by four segments of rope. The tension in the rope is assumed equal throughout its length (a good assumption for ropes in general since they weigh little). Three of the four rope segments are vertical while the remaining rope segment is at a small angle with the vertical. But for ease of calculation we can treat it as being exactly vertical. Since we are ignoring the mass of the pulleys, the tension in the four rope segments must equal the weight of the mass, in order to satisfy the condition of static equilibrium. Hence, 4F−Mg = 0. We then solve this equation for F.

Answer: F = Mg/4

---

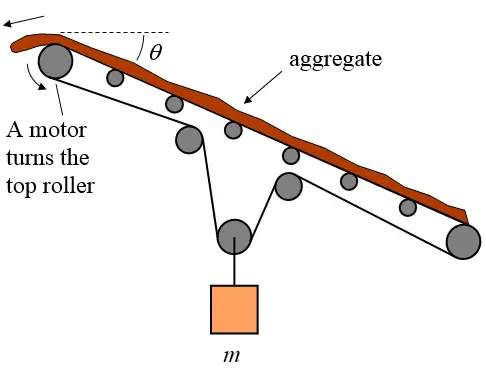
Bonus Problem

A conveyor belt carrying aggregate is illustrated in the figure below. A motor turns the top roller at a constant speed, and the remaining rollers are allowed to spin freely. The belt is inclined at an angle θ. To keep the belt in tension a weight of mass m is suspended from the belt, as shown.

Find the point of maximum tension in the belt. You don’t have to calculate it, just find the location and give a reason for it.



You can get the solution for this in PDF format. It's available through this link



Return to Physics Questions page


Return to Real World Physics Problems home page