About me and why I created this physics website.
Free Fall Problems
On this page I put together a collection of free fall problems to help you understand the concept of free fall better. The required equations and background reading to solve these problems are given here, for θ = 90°.Problem # 1
A ball is thrown with an initial upward velocity of 5 m/s. What is its velocity after 1.5 seconds, and what is the direction of velocity? Answer: 9.7 m/s, downward
Problem # 2
A researcher tests the acceleration due to gravity by dropping a pebble in an evacuated tube. After 0.5 seconds the pebble falls 1.226 meters. What is the acceleration due to gravity measured by the researcher? Answer: 9.808 m/s2
Problem # 3
Object A is located directly above Object B. Object B is dropped s seconds after Object A is dropped. As the two objects fall, the distance between them remains constant over time. What is the value of s ?
See answer
Problem # 4
Object A is located directly above Object B, and they are separated by a distance of 5 meters. Object A is thrown downward at a velocity of 1 m/s, and at the same time Object B is thrown upward at a velocity of 1 m/s. When do the two objects meet? Answer: At 2.5 seconds
Problem # 5
A ball is thrown upward at a velocity of 3.5 m/s. What is the greatest amount of time that must pass, after the ball is thrown, so that the ball is 0.25 meters above its launch point? Answer: 0.634 seconds
Problem # 6
In the figure below, solve for A, B, and C. Answer: A = 1, B = -19.6, C = -29.4
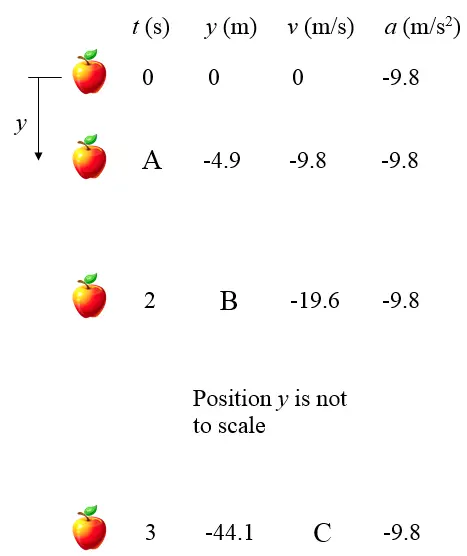
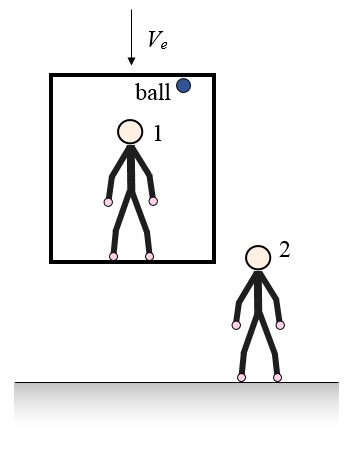
Problem # 7
Person 1 is inside an elevator, with inside height h, that is moving downward at a constant velocity of Ve. This person observes a ball drop from the top of the elevator to the bottom, while Person 2 is on the ground and also observes this. Based on the reference point of both persons, what is the simplest calculation that can be used to calculate the time it takes for the ball to fall from the top of the elevator to the bottom?
See answer
Answers For Free Fall Problems
Answer for Problem # 3
The value of s must be zero. For any other value, the distance between the objects would continuously be changing.
Answer for Problem # 7
The simplest calculation is based on the perspective of Person 1, since this person sees the ball fall from zero initial velocity (in his reference frame), and since the elevator is moving in a straight line at constant velocity, this is an inertial reference frame. This means that the falling time of the ball can be easily calculated by solving for t in the equation h = (1/2)gt2, so that t = (2h/g)1/2. Person 2 would of course calculate the same value of t, but it would be more difficult based on his reference frame since he sees the ball fall with an initial downward velocity equal to Ve, and along with having to determine the falling distance of the ball, which is greater than h in his reference frame, the calculation is made more complicated.
Return to Physics Questions page
Return to Real World Physics Problems home page