About me and why I created this physics website.

Torque Problems

On this page I put together a collection of torque problems to help you understand the concept of torque better. The required equations and background reading to solve these problems are given here.

Problem # 1

A force F acts at point P on a rigid body, as shown in the figure below, where r is the distance from point O to point P, and θ is the angle at which the force acts. What is the torque exerted on the rigid body about point O ? Answer: Frsinθ

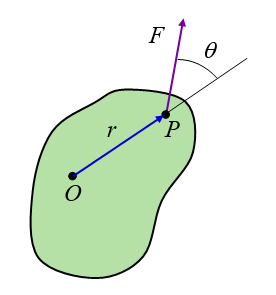
torque problem figure 1


Problem # 2

In the previous problem, suppose that r is a vector with components (3,2,0) in the xyz coordinate frame, and F is a vector with components (4,5,0). What is the torque exerted on the rigid body about point O, and what is the angle θ ?

See answer


Problem # 3

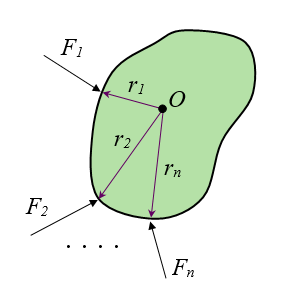
torque problem figure 2

In the figure above, consider the force vectors F1, F2,..., Fn, acting on the rigid body, and the corresponding arm vectors r1, r2,..., rn. Suppose this situation can be reduced to a resultant force FR, acting on the rigid body at point P, with resultant arm rR, plus a resultant force-couple torque TR, as shown in the figure below. Write a mathematical equation that equates the torque about point O, for the two scenarios.

See answer

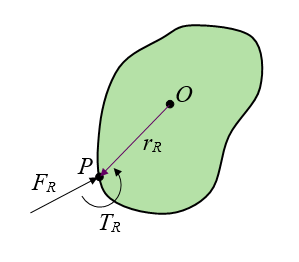
torque problem figure 3


Problem # 4

Try out this fun experiment related to bicycle physics (shown below). Stand a bicycle upright and orient one of the pedals so that it's at the bottom position. Next, push left on the pedal. Which way does the bicycle move?

See answer

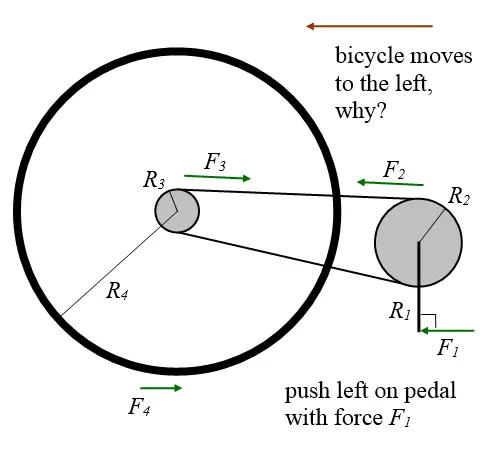
torque problem figure 4


Problem # 5

For a rocket in motion, the center of pressure P, caused by the air resistance at the bottom fins, is the resultant location of the pressure force caused by this air resistance. Show that the location of P below the center of mass of the rocket, at G, causes the rocket to be stable in flight, and not tumble through the air.

See answer

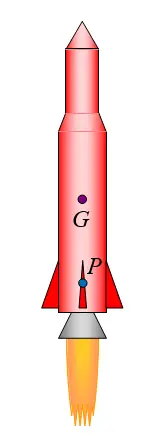
torque problem figure 5


Problem # 6

In the pulley arrangement shown in the figure below, a block of mass m is suspended from one end of a rope, and the other end of the rope is connected to a block of mass M, that is heavy enough to prevent movement. Rod OA makes an angle of 135° with each side of the platform. What is the torque exerted at point A, due to the forces acting on rod OA ? Assume the pulley has no friction.

See answer

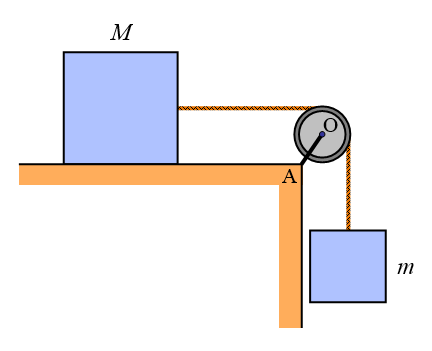
torque problem figure 7


Problem # 7

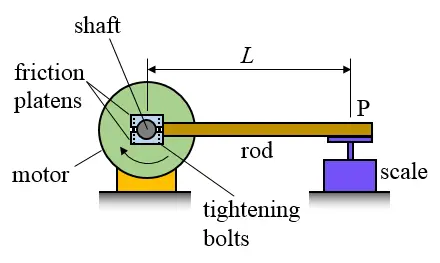
The torque of a motor is tested using the arrangement shown in the figure below. This is known as a "prony brake". In this set up, a pair of friction platens is tightened together against the motor shaft, and when the motor rotates in the direction shown, a force is exerted on the scale at point P, via a rod of length L. For a motor speed S, in revolutions per minute, and a scale reading of W, in Newtons, what is the power produced by the motor?

See answer

torque problem figure 8


Answers For Torque Problems

Answer for Problem # 2

The torque is equal to r×F = (3,2,0)×(4,5,0) = (0,0,7) (using cross-product multiplication), and since it's a positive number, the torque acts counterclockwise on the rigid body. The magnitude of r is denoted as |r| = (32+22)1/2 = 131/2, and the magnitude of F is denoted as |F| = (42+52)1/2 = 411/2. The magnitude of the torque is equal to 7, and by definition this is equal to |r||F|sinθ. Solve for θ = 17.65°.


Answer for Problem # 3

Mathematically speaking, this scenario can be expressed as r1×F1+r2×F2+...+rn×Fn = rRFR+TR, where FR = F1+F2+...+Fn.


Answer for Problem # 4

The bicycle moves to the left (which might be non-intuitive to you). Even though the force you are applying to the pedal turns the main crank clockwise, which is the direction required to move the bike to the right, the bicycle ends up moving left. This is because the external force F1 you are applying to the bike, results in a lesser force F4 in the opposite direction. Since F1 > F4, the bicycle moves left. Now, if you were to sit on the bike and apply a force F1 with your foot, the bicycle would move to the right since F1 is now an internal force in the bike-rider system and hence the only external force acting on the bicycle is F4 acting on the rear wheel, which pushes the bicycle to the right. This problem was taken directly from the bicycle physics page.


Answer for Problem # 5

Imagine the rocket is rotated by a small angle θ, as shown in the figure below.

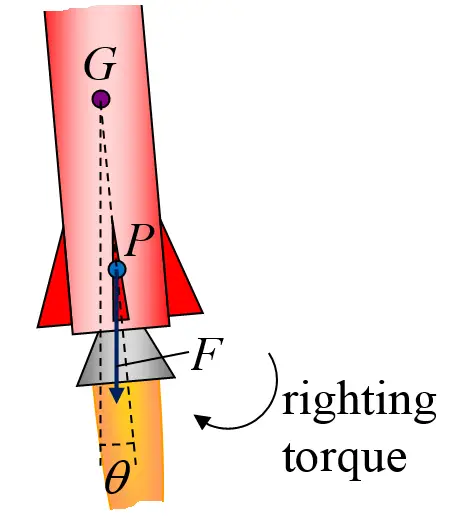
torque problem figure 6

For the angle of rotation shown, the resultant pressure force F acting through point P exerts a torque about the center of mass G of the rocket, equal to LGPFsinθ, where LGP is the arm length between points G and P. This torque, acting clockwise, rights the rocket back towards the vertical position, which causes the rocket to be aligned with its flight path, and remain stable during flight. If the angle of rotation θ was in the other direction, the resulting torque would act counterclockwise, and once more would right the rocket back towards the vertical position.


Answer for Problem # 6

By geometric symmetry, the two reaction forces acting on point O, caused by the horizontal and vertical rope tension, produce zero resultant torque about point A.


Answer for Problem # 7

The torque exerted by the motor is WL. Power is equal to the torque multiplied by the angular rotation speed of the motor, in radians/second. Therefore, power = WLSπ/30.



Return to Physics Questions page


Return to Real World Physics Problems home page