About me and why I created this physics website.
Relative Velocity Problems
On this page I put together a collection of relative velocity problems to help you understand relative velocity better.Problem # 1
A motorcycle traveling on the highway at a speed of 120 km/h passes a car traveling at a speed of 90 km/h. From the point of view of a passenger on the car, what is the velocity of the motorcycle? Answer: 30 km/h
Problem # 2
A ball is kicked off the back of a pickup truck traveling at 50 km/h. A pedestrian on the ground sees the ball hit the pavement and then bounce straight up. What was the velocity of the ball relative to the truck?
See answer
Problem # 3
A duck swims at a constant speed from one side of a river to the other side in a time of 4 seconds. The river is 6 meters wide and it is flowing at a speed of 2 m/s. What is the velocity of the duck and what is its direction of travel, with respect to ground?
See answer
Problem # 4
Why is it easier for an airplane to take off into the wind?
See answer
Problem # 5
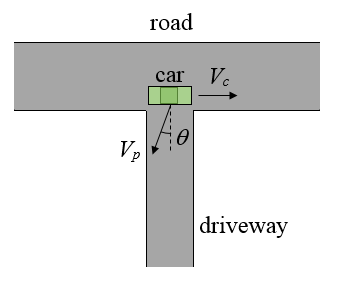
A car is driving down the road at a velocity Vc, relative to ground, and is delivering newspapers to homes, as shown in the figure below. The newspapers are thrown at a velocity of Vp relative to the car. At what angle θ must the newspapers be thrown, relative to the car, so that they fly in a direction parallel to the driveways?
See answer
Problem # 6
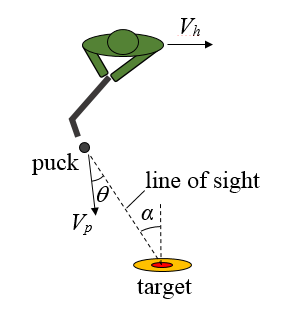
In a skills competition, a hockey player is skating across the ice at a velocity Vh and tries to hit a target with the puck, as shown in the figure below. If the velocity of the puck relative to the player is Vp, at what angle θ must the player hit the puck, relative to the line of sight between puck and target, so that the puck hits the target?
See answer
Problem # 7
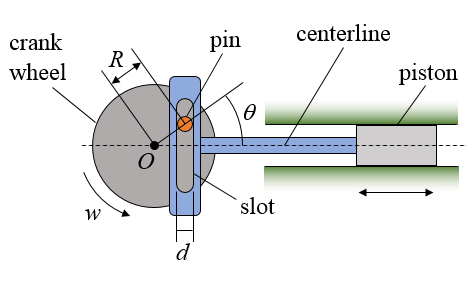
A scotch yoke mechanism is shown in the figure below, with dimensions given in units of meters. The pin is rigidly connected to the crank wheel which is rotating at w radians per second. Since the scotch yoke is being used in a food plant and contamination must be prevented, the pin is made of smooth plastic, with no lubrication applied. To prevent excessive frictional heating, the sliding velocity of the pin relative to the slot is to be no more than 5 m/s. What is the maximum value of w to make sure this limit is not exceeded?
See answer
Answers For Relative Velocity Problems
Answer for Problem # 2
You first have to assume that the truck velocity and relative ball velocity are both in the horizontal direction, since no additional information is given. For the ball to bounce straight up, it would need essentially zero horizontal velocity relative to the ground, which means that the velocity of the ball relative to the truck was 50 km/h. Note that this assumes that the ball is not spinning, since spin would cause the ball to deflect sideways after bouncing off the pavement.
Answer for Problem # 3
Since the duck is swimming at constant speed across the river, and with respect to it, its speed is 6/4 = 1.5 m/s with respect to the river. The river is flowing at a speed of 2 m/s (with respect to ground), so the magnitude of the velocity of the duck with respect to ground can be found using the Pythagorean theorem, which is then V = (1.52 + 22)1/2 = 2.5 m/s. Using trigonometry, the direction of this velocity is tan-1(1.5/2) = 36.9°, with respect to ground, and measured relative to the direction of flow of the river.
Answer for Problem # 4
For an airplane to generate aerodynamic lift, there must be a high enough relative velocity between the wings and the air. If an airplane takes off by traveling into the wind, it does not have to travel as quickly with respect to ground. This in turn means that it can take off over a shorter travel distance over the runway than if there was no wind present.
Answer for Problem # 5
For the newspapers to fly parallel to the driveways when they are airborne, the component of velocity of Vp that is parallel to the road must cancel out with Vc, so that the velocity of the newspaper with respect to ground is in a direction parallel to the driveways. Using trigonometry, this means that Vpsinθ = Vc, and θ = sin-1(Vc/Vp).
Answer for Problem # 6
For the puck to hit the target, it must travel along the line of sight. This means that the component of velocity of Vp that is orthogonal to the line of sight, must cancel out with the component of velocity of Vh that is orthogonal to the line of sight. This means that the puck travels along the line of sight, with respect to ground (or rather, with respect to the ice), and hits the target. Using trigonometry, this means that Vpsinθ = Vhcosα, and θ can be solved for.
Answer for Problem # 7
This is a tricky problem! You have to recognize that the pin both rotates and translates relative to the slot, which both contribute to the sliding velocity relative to the slot. The pin makes contact with both sides of the slot at the same time, but we only need to consider contact with one side of the slot, so let's choose the right side. Let's also choose a sign convention where up is positive and down is negative. Now, the pin rotates counterclockwise, at an angular velocity of w, relative to the slot, and this contributes a sliding velocity of w×(pin radius) = wd/2 relative to the slot (on the right side). In addition, the pin translates relative to the slot, and this contributes a sliding velocity of wRcosθ relative to the slot. The sliding velocity Vrel of the pin relative to the right side of the slot is then Vrel = wd/2 + wRcosθ. This is a maximum when θ = 0°, which then results in maximum Vrel = w(d/2 + R). This value is not to exceed 5 m/s, so the maximum rotation rate of the crank wheel is w = 5/(d/2 + R).
Return to Physics Questions page
Return to Real World Physics Problems home page