About me and why I created this physics website.

Inclined Plane Problems

On this page I put together a collection of inclined plane problems to help you better understand the physics behind them. The required equations and background reading to solve these problems are given under the following pages: rigid body dynamics, center of mass, and friction.

Problem # 1

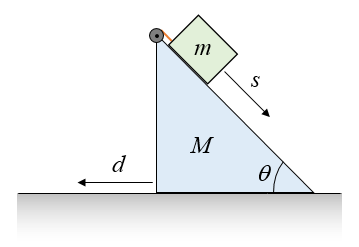
A physicist sets up an experiment to determine the mass of a block, as shown in the figure below. In this experiment, the block is placed on top of a stationary incline, of mass M, and slowly released with a motor and pulley system, causing the block to slide down the incline a distance s. As a result, the incline slides to the left a distance d, on a well lubricated platform. If the mass of the motor and pulley system can be neglected, what is the mass m of the block?

See answer




Problem # 2

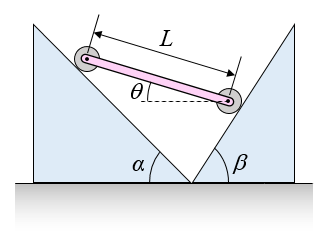
A linkage of length L and mass m, which has two wheels on the ends, is placed between two inclines at an angle θ, as shown in the figure below. For α = 30°, β = 45°, L = 0.75 m, and m = 1.5 kg, what is the angle θ so that the linkage remains stationary?

See answer




Problem # 3

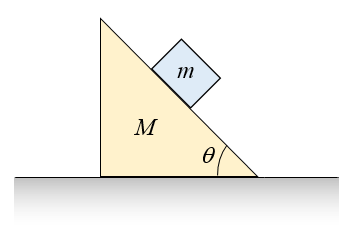
A block of mass m is placed on an incline of mass M, as shown in the figure below. The coefficient of kinetic friction between the block and incline is μ_k. What is the minimum coefficient of static friction between the incline and floor, so that the incline doesn't slide on the floor when the block slides down the incline?

See answer




Problem # 4

Referring to the previous problem, suppose that the incline slides to the left when the block slides down the incline. If the coefficient of kinetic friction between the floor and incline is μ_k2, what is the acceleration of the incline?

See answer


Problem # 5

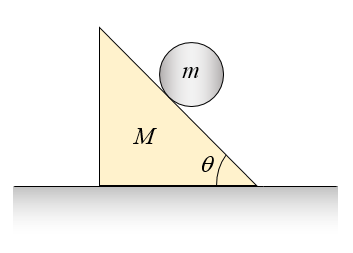
A solid cylinder of mass m and radius r is placed on an incline of mass M, as shown in the figure below. What is the minimum coefficient of static friction between the incline and floor, so that the incline doesn't slide on the floor when the cylinder rolls down the incline, without slipping?

See answer




Problem # 6

Referring to the previous problem, suppose that the incline slides to the left when the cylinder rolls down the incline, without slipping. If the coefficient of kinetic friction between the floor and incline is μ_k, what is the acceleration of the incline?

See answer


Problem # 7

Referring to problem # 5, at what acceleration must the incline be pushed along the floor so that the cylinder does not roll on the incline?

See answer


Answers For Inclined Plane Problems

Answer for Problem # 1

Since the platform is well lubricated, we can assume that there is negligible friction between the incline and platform. This then means that there are no external forces, in the horizontal direction, acting on the system - comprised of incline, block, and motor/pulley (the mass of which can be ignored). The horizontal position of the center of mass of the system must then remain fixed. For convenience, choose an arbitrary reference point to the left of (or right of) the system. Let x_M be the initial horizontal position of the center of mass of the incline, measured from this reference point, and let x_m be the initial horizontal position of the center of mass of the block, measured from this reference point. The following equation then equates the position of the center of mass of the system before and after the block slides down the incline.

Mx_M + mx_m = M(x_M − d) + m(x_m + scosθ − d)

Solve for m:

m = Md/(scosθ − d)


Answer for Problem # 2

The wheels can't support torque about their center of rotation, so there is no force parallel to the incline at the contact point between wheel and incline. So there is only a normal force at the contact point between wheel and incline, as shown in the free body diagram below. The normal forces are N₁ and N₂, and they are acting on the linkage.



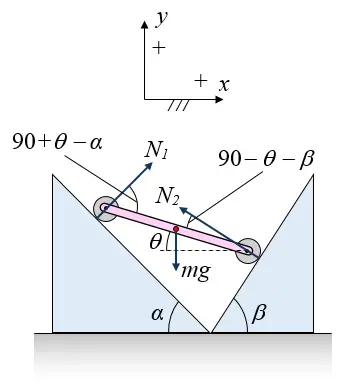
where g is the acceleration due to gravity

The torque about the center of mass (denoted by the red dot) of the linkage is

-N₁(L/2)sin(90°+θ−α) + N₂(L/2)sin(90°−θ−β) = 0        (1)

The sum of the forces in the x-direction is

N₁sinα − N₂sinβ = 0        (2)

The sum of the forces in the y-direction is

N₁cosα + N₂cosβ − mg = 0        (3)

Combine equations (1)-(3) to solve for θ, using the given values. We have

θ = -20.1° (the negative sign means that the linkage is instead sloped such that the right end is raised higher than the left end, at an angle of 20.1° with the horizontal)


Answer for Problem # 3

The free body diagram below shows the setup of the problem.



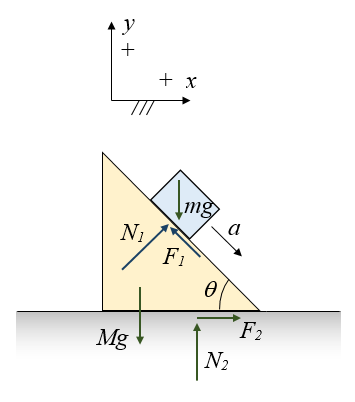
where:

N₁ is the normal force acting on the block, due to contact with the incline

F₁ is the friction force acting on the block, due to contact with the incline

a is the acceleration of the block down the incline

g is the acceleration due to gravity

N₂ is the normal force acting on the incline, due to contact with the floor

F₂ is the friction force acting on the incline, due to contact with the floor

For the block, the sum of the forces in the x-direction is

N₁sinθ − F₁cosθ = macosθ        (1)

For the block, the sum of the forces in the y-direction is

N₁cosθ + F₁sinθ − mg = -masinθ        (2)

From Newton's third law, the forces N₁ and F₁ act on the incline in the opposite direction to that shown in the figure above.

For the incline, the sum of the forces in the x-direction is

-N₁sinθ + F₁cosθ + F₂ = 0        (3)

For the incline, the sum of the forces in the y-direction is

-N₁cosθ − F₁sinθ − Mg + N₂ = 0        (4)

There is kinetic friction between the block and incline, so

F₁ = μ_kN₁        (5)

Combine equations (1), (2), and (5) to solve for N₁ and F₁. Then substitute these into equations (3) and (4) to solve for N₂ and F₂. Then, the minimum coefficient of static friction between incline and floor is

μ_s = F₂/N₂

and

μ_s = A/B

where:

A = m(sinθ−μ_kcosθ)

B = m(cosθ+μ_ksinθ) + M/cosθ


Answer for Problem # 4

The free body diagram below shows the setup of the problem.



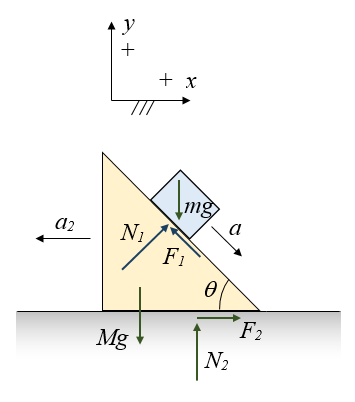
where:

N₁ is the normal force acting on the block, due to contact with the incline

F₁ is the friction force acting on the block, due to contact with the incline

a is the acceleration of the block down the incline, and relative to it

a₂ is the acceleration of the incline along the floor

g is the acceleration due to gravity

N₂ is the normal force acting on the incline, due to contact with the floor

F₂ is the friction force acting on the incline, due to contact with the floor

For the block, the sum of the forces in the x-direction is

N₁sinθ − F₁cosθ = m(acosθ + a₂)        (1)

Note: On the right side of the above equation, (acosθ + a₂) is the horizontal acceleration of the block with respect to ground. Acceleration must always be evaluated relative to an inertial reference frame (such as ground), when applying Newton's second law (i.e. F = ma).

For the block, the sum of the forces in the y-direction is

N₁cosθ + F₁sinθ − mg = -masinθ        (2)

From Newton's third law, the forces N₁ and F₁ act on the incline in the opposite direction to that shown in the figure above.

For the incline, the sum of the forces in the x-direction is

-N₁sinθ + F₁cosθ + F₂ = Ma₂        (3)

For the incline, the sum of the forces in the y-direction is

-N₁cosθ − F₁sinθ − Mg + N₂ = 0        (4)

There is kinetic friction between the block and incline, so

F₁ = μ_kN₁        (5)

There is kinetic friction between the floor and incline, so

F₂ = μ_k2N₂        (6)

Combine equations (1)-(6) to solve for a₂. The result is

a₂ = A/B

where:

A = mgcosθ(μ_kcosθ−sinθ) + μ_k2(cosθ+μ_ksinθ)mgcosθ + Mgμ_k2

B = M − msinθ(μ_kcosθ−sinθ) − μ_k2(cosθ+μ_ksinθ)msinθ


Answer for Problem # 5

The free body diagram below shows the setup of the problem.



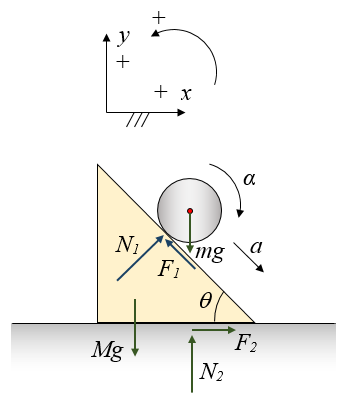
where:

N₁ is the normal force acting on the cylinder, due to contact with the incline

F₁ is the friction force acting on the cylinder, due to contact with the incline

a is the acceleration of the center of mass of the cylinder as it rolls down the incline

α is the angular acceleration of the cylinder as it rolls down the incline

g is the acceleration due to gravity

N₂ is the normal force acting on the incline, due to contact with the floor

F₂ is the friction force acting on the incline, due to contact with the floor

For the cylinder, the sum of the forces in the x-direction is

N₁sinθ − F₁cosθ = macosθ        (1)

For the cylinder, the sum of the forces in the y-direction is

N₁cosθ + F₁sinθ − mg = -masinθ        (2)

The torque about the center of mass (denoted by the red dot) of the cylinder is

-F₁r = I_G(α)        (3)

where I_G is the rotational inertia of the (solid) cylinder about the center of mass, and I_G = (1/2)mr²

Based on the kinematics we can write,

-α = a/r        (4)

From Newton's third law, the forces N₁ and F₁ act on the incline in the opposite direction to that shown in the figure above.

For the incline, the sum of the forces in the x-direction is

-N₁sinθ + F₁cosθ + F₂ = 0        (5)

For the incline, the sum of the forces in the y-direction is

-N₁cosθ − F₁sinθ − Mg + N₂ = 0        (6)

Combine equations (1)-(4) to solve for N₁ and F₁. Then substitute these into equations (5) and (6) to solve for N₂ and F₂. Then, the minimum coefficient of static friction between incline and floor is

μ_s = F₂/N₂

μ_s = macosθ/(Mg+mg−masinθ)

where a = (2/3)gsinθ


Answer for Problem # 6

The free body diagram below shows the setup of the problem.



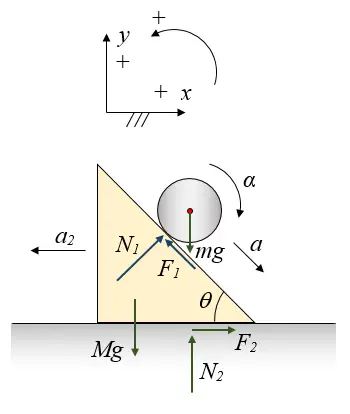
where:

N₁ is the normal force acting on the cylinder, due to contact with the incline

F₁ is the friction force acting on the cylinder, due to contact with the incline

a is the acceleration of the center of mass of the cylinder, as it rolls down the incline. This acceleration is relative to the incline

a₂ is the acceleration of the incline along the floor

α is the angular acceleration of the cylinder as it rolls down the incline (with respect to ground)

g is the acceleration due to gravity

N₂ is the normal force acting on the incline, due to contact with the floor

F₂ is the friction force acting on the incline, due to contact with the floor

For the cylinder, the sum of the forces in the x-direction is

N₁sinθ − F₁cosθ = m(acosθ + a₂)        (1)

For the cylinder, the sum of the forces in the y-direction is

N₁cosθ + F₁sinθ − mg = -masinθ        (2)

The torque about the center of mass (denoted by the red dot) of the cylinder is

-F₁r = I_G(α)        (3)

where I_G is the rotational inertia of the (solid) cylinder about the center of mass, and I_G = (1/2)mr²

Based on the kinematics we can write,

-α = a/r        (4)

From Newton's third law, the forces N₁ and F₁ act on the incline in the opposite direction to that shown in the figure above.

For the incline, the sum of the forces in the x-direction is

-N₁sinθ + F₁cosθ + F₂ = Ma₂        (5)

For the incline, the sum of the forces in the y-direction is

-N₁cosθ − F₁sinθ − Mg + N₂ = 0        (6)

There is kinetic friction between the floor and incline, so

F₂ = μ_kN₂        (7)

Combine equations (1)-(7) to solve for a₂. The result is

a₂ = A/B

where:

A = (2/3)gsinθ(mcosθ+μ_kmsinθ) − μ_k(M+m)g

B = (2/3)cosθ(mcosθ+μ_kmsinθ) − m − M


Answer for Problem # 7

For convenience, refer to the free body diagram in the previous answer. If the cylinder doesn't roll on the incline this means that a = 0, and α = 0 - from the torque equation, this means that F₁ = 0.

For the cylinder, the sum of the forces in the x-direction is

N₁sinθ = ma₂        (1)

For the cylinder, the sum of the forces in the y-direction is

N₁cosθ − mg = 0        (2)

From equations (1) and (2) we can solve for a₂, which is the acceleration of the incline. This is equal to the acceleration of the cylinder, since the incline and cylinder move together as a single unit.

So,

a₂ = gtanθ (this is the required acceleration of the incline, to the right)



Return to Physics Questions page


Return to Real World Physics Problems home page