About me and why I created this physics website.
Kinetic Energy Problems
On this page I put together a collection of kinetic energy problems to help you understand the concept of kinetic energy better. The required equations and background reading to solve these problems are given here.
Problem # 1
Two solid uniform cylinders are connected with a belt wrapped around both cylinders, as shown in the figure below. The mass and radius of the smallest cylinder is mA and rA, respectively, and the mass and radius of the largest cylinder is mB and rB, respectively. When the cylinders are rotating, what is the ratio of the kinetic energy of the largest cylinder to the kinetic energy of the smallest cylinder?
See answer
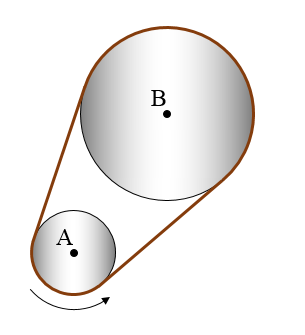
Problem # 2
In the previous problem, suppose that the distance between the center of both cylinders, A and B, is equal to d, and the linear density of the belt is ρ. What is the kinetic energy of the belt if the smallest cylinder is rotating at a speed of S revolutions per minute?
See answer
Problem # 3
In the figure below, a liquid is shown flowing through a horizontal pipe in steady-state fashion. The cross-sectional area of the pipe at location A is larger than at location B. Using the Bernoulli equation and the concept of mass conservation, explain why there is a difference in the kinetic energy of the liquid between locations A and B.
See answer
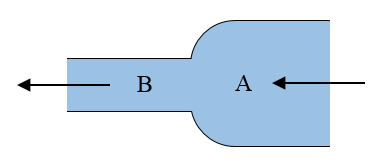
Problem # 4
In the figure below, wind is blowing through a wind turbine at constant velocity v1 upstream of the wind turbine, and at constant velocity v2 downstream of the wind turbine. What is the maximum kinetic energy that the wind turbine can obtain, as a percentage of the kinetic energy of the wind upstream of the wind turbine?
See answer
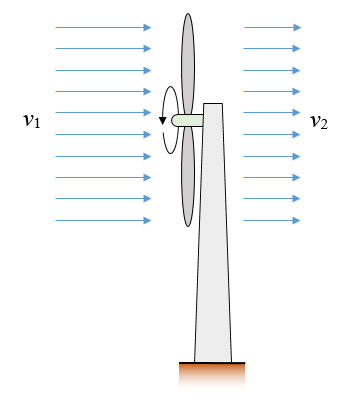
Problem # 5
The figure below shows a linkage with a wheel on each end, and each wheel can move freely inside two slots that are perpendicular to each other. The mass of the linkage is m, its rotational inertia about the center of mass is IG, its length is L, and the angle that the linkage makes with the bottom slot is θ. If the bottom wheel is pulled to the left at a constant velocity v, what is the kinetic energy of the linkage as a function of θ ? Ignore the mass of the wheels. Note that 0 < θ < 90° .
See answer
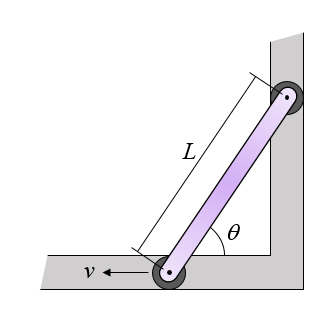
Problem # 6
A car is traveling on the highway at a speed S. The body of the car, and driver, have a combined mass of M, the mass of each wheel is m, the radius of each wheel is r, and the rotational inertia of each wheel about the center of mass is IG. What is the total kinetic energy of the car?
See answer
Problem # 7
A plane is flying in a straight line at a velocity of v, relative to the ground, and the propeller is rotating at a speed of w radians per second. If the mass of the propeller is m, and the rotational inertia of the propeller about its mass center is IG, what is the kinetic energy of the propeller?
See answer
Answers For Kinetic Energy Problems
Answer for Problem # 1
The kinetic energy of the smallest cylinder is KEA = (1/2)IAwA2, where IA is the rotational inertia about the center, and wA is the angular velocity. Now, IA = (1/2)mArA2. Similarly, for the largest cylinder, the kinetic energy is KEB = (1/2)IBwB2. Now, IB = (1/2)mBrB2. Since the two cylinders are connected with a belt, their linear velocities are equal, which means that wArA = wBrB. The desired kinetic energy ratio is KEB/KEA. After substituting the above relations, and simplifying, the kinetic energy ratio becomes KEB/KEA = mB/mA.
Answer for Problem # 2
Let's say the length of the belt is L, which can be determined from the geometry of the problem (not shown here since it's quite involved and doesn't add to the understanding of the problem). Then the mass of the belt is mbelt = Lρ. The angular velocity of the smallest cylinder is wA = Sπ/30, in units of radians/second. The linear velocity of the belt is then vbelt = wArA, and since this is a scalar quantity which is the same at every location on the belt, the kinetic energy of the belt is (1/2)mbeltvbelt2.
Answer for Problem # 3
According to the Bernoulli equation, (1/2)VB2 − (1/2)VA2 = (PA − PB)/ρ. Since the cross-sectional area at location B is less than at location A, then VB > VA, by mass conservation. Therefore, according to the Bernoulli equation, the kinetic energy, per unit mass of liquid, at location B is greater than at location A. This means that the fluid pressure at location A is greater than the fluid pressure at location B.
Answer for Problem # 4
The answer is 59.3%. The solution to this problem comes from the well known Betz' Law for wind turbines, which can be easily referenced online. Take the time to look this up, since it's an interesting problem, originally solved by Albert Betz in 1919.
Answer for Problem # 5
To make things easier to visualize, first imagine an xy-coordinate system with origin located at the bottom right corner, where the line of travel of the center-point of both wheels meet, and positions to the left of, and above, this point are considered positive. Then, the x-position of the center of mass of the linkage is x = (1/2)Lcosθ, and the y-position of the center of mass is y = (1/2)Lsinθ. Now, take the derivative with respect to time to obtain velocity. So, dx/dt = v/2 = -(1/2)Lsinθ(dθ/dt) (equation 1), and dy/dt = (1/2)Lcosθ(dθ/dt) (equation 2). From equation 1, solve for dθ/dt = -v/(Lsinθ). Substitute this into equation 2 and we get, dy/dt = -(1/2)v/(tanθ). The kinetic energy of the linkage is then KE = (1/2)IG(dθ/dt)2 + (1/2)m((dx/dt)2 + (dy/dt)2).
Answer for Problem # 6
The total kinetic energy of the car is equal to the kinetic energy of the car body + driver + wheels. Therefore, KE = (1/2)MS2 + 4×(1/2)IGw2 + 4×(1/2)mS2, where w is the angular velocity of each wheel, which is equal to w = S/r.
Answer for Problem # 7
The kinetic energy of the propeller is equal to KE = (1/2)mv2 + (1/2)IGw2.
Return to Physics Questions page
Return to Real World Physics Problems home page