About me and why I created this physics website.

Force Problems

On this page I put together a collection of force problems to help you understand forces better. The required equations and background reading to solve these problems are given on the friction page, the equilibrium page, and Newton's second law page.

Problem # 1

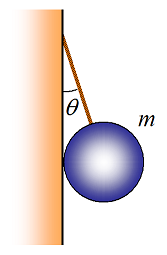
A ball of mass m is hanging on a wall with a string, as shown. The string makes an angle θ with the wall. What is the tension in the string? Answer: mg/cosθ




Problem # 2

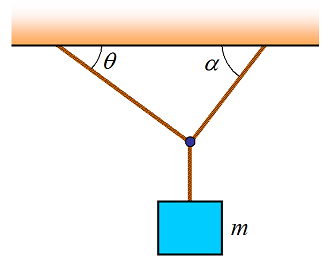
A block of mass m is hanging off the ceiling using three strings, as shown. What is the tension in the three strings? Answer: Bottom string tension is mg, right string tension is mg/(sinα+cosαtanθ), left string tension is mg/(sinθ+cosθtanα)




Problem # 3

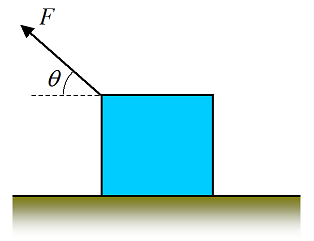
A block of mass M is being pulled at constant velocity on a horizontal floor with a force F, at angle θ as shown. The coefficient of kinetic friction is μ_k, between block and floor. Determine the force F. Answer: F = Mgμ_k/(cosθ+μ_ksinθ)




Problem # 4

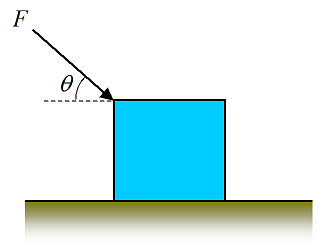
A block of mass M is being pushed at constant velocity on a horizontal floor with a force F, at angle θ as shown. The coefficient of kinetic friction is μ_k, between block and floor. Determine the force F. Answer: F = Mgμ_k/(cosθ−μ_ksinθ)




Problem # 5

A block of mass M is being pulled at constant velocity on a horizontal floor with a force F. The coefficient of kinetic friction is μ_k, between block and floor. Determine the force F. Answer: F = Mgμ_k




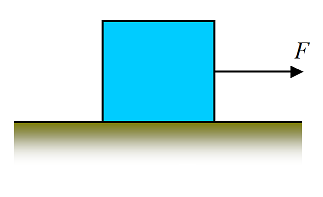
Problem # 6

A block is lying on a horizontal floor. The weight of the block is W. What is the normal force N between the block and floor? Answer: N = W




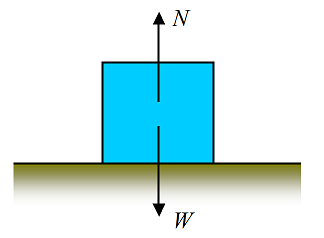
Problem # 7

A block of mass M is sitting on a surface inclined at angle θ. Given that the coefficient of static friction is μ_s between block and surface, what is the maximum angle θ so that the block doesn't slide?

Hint and answer




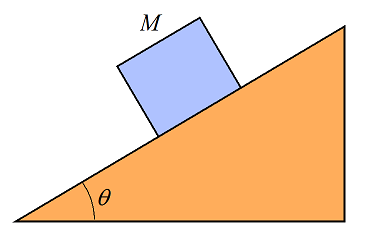
Problem # 8

Two blocks of mass M and m are sitting on a surface inclined at angle θ. The blocks are touching. The coefficient of static friction between the smaller block and the surface is μ_s1, and the coefficient of static friction between the larger block and the surface is μ_s2. Formulate a mathematical inequality for the condition that no sliding occurs. There may be more than one inequality.

Hint and answer




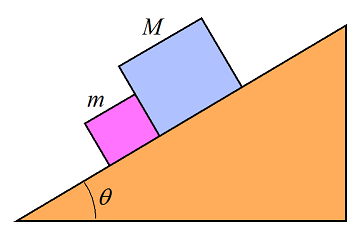
Problem # 9

Two blocks of mass M and m are sitting on a horizontal floor. The blocks are touching. The coefficient of static friction between the smaller block and the floor is μ_s1, and the coefficient of static friction between the larger block and the floor is μ_s2. What is the minimum push force F so that the blocks begin to move? Answer: F_min = Mgμ_s2+mgμ_s1




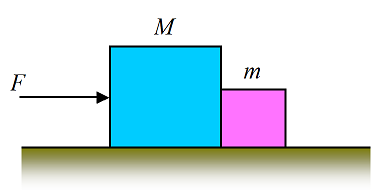
Problem # 10

A block of mass m is sitting on a block of mass M. The bottom block is sitting on a horizontal floor. The coefficient of static friction between the blocks is μ_s1, and the coefficient of static friction between the bottom block and the floor is μ_s2. What is the minimum pull force F on the bottom block so that the blocks begin to move? Given that the coefficient of kinetic friction between the bottom block and the floor is μ_k, what is the maximum pull force F so that there is no slipping between the blocks?

Hint and answer




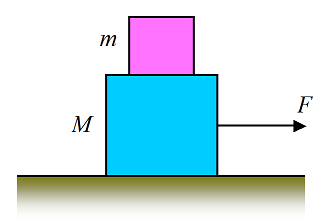
The hints and answers for these force problems will be given next.

Hints And Answers For Force Problems


Hint and answer for Problem # 7

The force of gravity pulling down on the block is F₁ = Mgsinθ. The maximum friction force opposing the sliding is F₂ = Mgcosθμ_s. At some angle θ the block will be on the verge of sliding. This is the maximum angle θ and occurs when F₁ = F₂. The maximum angle θ can be solved from this.

Answer: θ_max = atan(μ_s)


Hint and answer for Problem # 8

There are two cases to consider:

Case 1: If μ_s1 ≤ μ_s2 then the limiting case for no sliding occurs when θ = θ_max (where θ_max = atan(μ_s1), using the solution in Problem # 7). Therefore, for μ_s1 ≤ μ_s2, θ ≤ atan(μ_s1), for no sliding.

Case 2: If μ_s1 > μ_s2 then sliding occurs only if the blocks slide down together, with the larger block pushing against the smaller block in front. The limiting case is when this is on the brink of happening, and the static friction is at its limit for both blocks. Since the blocks move together we can analyze them as one unit. The equation for static equilibrium along the plane of the incline is: (M+m)gsinθ−Mgcosθμ_s2−mgcosθμ_s1 = 0. From this equation we can solve for θ, and this is the maximum angle θ for μ_s1 > μ_s2, for which there is no sliding.

Answer: For μ_s1 ≤ μ_s2, θ ≤ atan(μ_s1). For μ_s1 > μ_s2, θ ≤ atan{(Mμ_s2+mμ_s1)/(M+m)}


Hint and answer for Problem # 10

The blocks begin sliding when the force F is just large enough to overcome the static friction between the bottom block and floor. This force is the minimum pull force.

The maximum pull force corresponds to the maximum acceleration that the blocks can experience without the top block slipping off the bottom block. By Newton's second law, the force exerted on the top block due to contact with the bottom block is F_top = ma, where a is the acceleration of the blocks. Applying Newton's second law to the bottom block we have: F−(M+m)gμ_k−F_top = Ma. To avoid slipping, the maximum value of F_top is F_top = mgμ_s1. This corresponds to the maximum acceleration and hence the maximum pull force. Combine the above three equations to solve for the maximum pull force.

Answer: F_min = (M+m)gμ_s2, F_max = (M+m)gμ_k+mgμ_s1(1+M/m)

---

Bonus Problems Related to Forces

1. Is it possible to lift a car using fire hoses?

2. Can a sailboat stranded in calm water start moving by blowing air into its sail with an onboard fan?

I created a physics analysis for these two problems, in PDF format. It's available through this link.



Return to Physics Questions page


Return to Real World Physics Problems home page