About me and why I created this physics website.
Statics Problems
On this page I put together a collection of statics problems to help you understand static equilibrium better. The required equations and background reading to solve these problems is given on the equilibrium page.Problem # 1
A ball of mass 10 kg is hanging vertically from a string. What is the tension in the string? (Answer: 98 N)
Problem # 2
Two boxes are stacked on the floor, one on top of the other. The top box has a mass of 10 kg and the bottom box has a mass of 25 kg. What is the contact force between the boxes, and what is the contact force between the bottom box and the floor? (Answer: 98 N, 343 N)
Problem # 3
The ball in problem # 1 is hung vertically from two strings. What is the tension in the strings? (Answer: 49 N)
Problem # 4
A chain of mass 2 kg is resting on a table with half of its length hanging over the edge of the table. What force does the chain exert on the table? (Answer: 19.6 N)
Problem # 5
A painting of mass 3 kg is hung off a wall with two strings attached to the top two corners of the painting. Each string makes an angle of 45 degrees with the ceiling. What is the tension in the strings? (Answer: 20.79 N)
Problem # 6
The general equation for drag acting on a body is given by D = (1/2)CρAv2, where C is the drag coefficient, ρ is the density of the fluid through which the body is moving, v is the speed of the body relative to the fluid, and A is the projected cross-sectional area of the body perpendicular to the flow direction.
For a skydiver of mass m, what is the constant (terminal) speed reached during the fall?
(For the answer see the physics of skydiving page)
Problem # 7
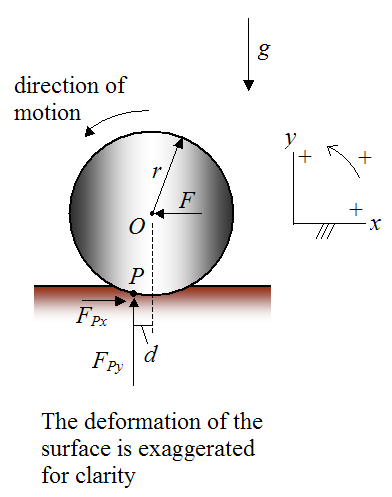
A cylinder of mass m and radius r is being pushed on flat ground at constant speed without slipping, with a horizontal force F acting at the geometric center O of the cylinder. The resultant force acting on the cylinder due to contact with the ground acts through point P, which is a small horizontal distance d from point O, as shown. This resultant force can be broken down into horizontal and vertical components FPx and FPy, as shown. Since the cylinder is rolling at constant velocity with no slipping, its angular acceleration is zero and its center of mass (coinciding with point O) has zero acceleration. Hence this can be treated as a statics problem. Find an expression for the force F.
(For the answer click here)
Problem # 8
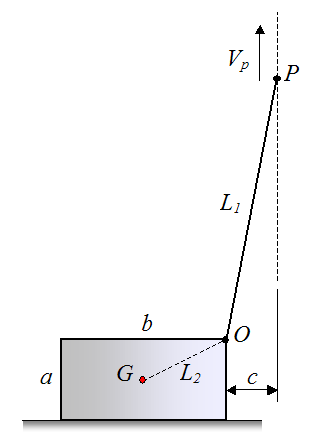
A heavy pump casing with a mass m is to be lifted off the ground using a crane. For simplicity, the motion is assumed to be two-dimensional, and the pump casing is represented by a rectangle having side dimensions ab (see figure). A cable of length L1 is attached to the crane (at point P) and the pump casing (at point O). The crane pulls up vertically on the cable with a constant velocity Vp.
The center of mass G of the pump casing is assumed to lie in the center of the rectangle. It is located at a distance L2 from point O. The right side of the pump casing is located at a horizontal distance c from the vertical line passing though point P.
Find the maximum cable tension during the lift, for the part of the lift before the pump casing loses contact with the ground (lift off).
Evaluate for a specific case where:
a = 0.4 m
b = 0.6 m
c = 0.2 m
L1 = 3 m
m = 200 kg
Assume:
• The friction between the pump casing and ground is high enough so that the pump casing does not slide along the ground (towards the right), before lift off occurs.
• Before lift off occurs, dynamic effects are negligible and this can be treated as a statics problem.
• The mass of the cable can be neglected.
(Answer: The maximum cable tension is 1994 N, before lift off occurs)
Return to Physics Questions page
Return to Real World Physics Problems home page
