Physics Questions
On this page I put together a collection of physics questions to help you understand physics better. These questions are designed to challenge and inspire you to think about physics at a deeper level. In addition to being challenging, these questions are fun and interesting. This page is a good resource for students who want good quality problems to practice with when studying for tests and exams.To see the questions click on the category you are interested in:
High School Physics Questions
College and University Physics Questions
Extra Challenging Physics Questions
High School Physics Questions
Problem # 1
Do heavier objects fall more slowly than lighter objects?
See solution
Problem # 2
Why do objects float in liquids denser than themselves?
See solution
Problem # 3
A particle is moving around in a circle and its position is given in polar coordinates as x = Rcosθ, and y = Rsinθ, where R is the radius of the circle, and θ is in radians. From these equations derive the equation for centripetal acceleration.
See solution
Problem # 4
How come in free fall you feel weightless even though gravity is pulling down on you? (ignore air resistance when answering this question).
See solution
Problem # 5
What is the difference between centripetal acceleration and centrifugal force?
See solution
Problem # 6
What is the difference between energy and power?
See solution
Problem # 7
Two identical cars collide head on. Each car is traveling at 100 km/h. The impact force on each car is the same as hitting a solid wall at:
(a) 100 km/h
(b) 200 km/h
(c) 150 km/h
(d) 50 km/h
See solution
Problem # 8
Why is it possible to drive a nail into a piece of wood with a hammer, but it is not possible to push a nail in by hand?
See solution
Problem # 9
An archer pulls back 0.75 m on a bow which has a stiffness of 200 N/m. The arrow weighs 50 g. What is the velocity of the arrow immediately after release?
See solution
Problem # 10
When a moving car encounters a patch of ice the brakes are applied. Why is it desirable to keep the wheels rolling on the ice without locking up?
See solution
Solutions For High School Physics Questions
Solution For Problem # 1
No. If an object is heavier the force of gravity is greater, but since it has greater mass the acceleration is the same, so it moves at the same speed (if we neglect air resistance). If we look at Newton's second law, F = ma. The force of gravity is F = mg, where m is the mass of the object and g is the acceleration due to gravity.
Equating, we have mg = ma. Therefore, a = g.
If there was no air resistance, a feather would fall at the same speed as an apple.
Solution For Problem # 2
If an object were completely immersed in a liquid denser than it, the resulting buoyant force would exceed the weight of the object. This is because the weight of the liquid displaced by the object is greater than the weight of the object (since the liquid is denser). As a result, the object cannot remain completely submerged and it floats. The scientific name for this phenomenon is Archimedes Principle.
Solution For Problem # 3
Without loss of generality, we only need to look at the equation for the x-position, since we know that centripetal acceleration points towards the center of the circle. Thus, when θ = 0, the second derivative of x with respect to time must be the centripetal acceleration.
The first derivative of x with respect to time t is:
dx/dt = -Rsinθ(dθ/dt)
The second derivative of x with respect to time t is:
d2x/dt2 = -Rcosθ(dθ/dt)2−Rsinθ(d2θ/dt2)
In both of the above equations the chain rule of Calculus is used and by assumption θ is a function of time. Therefore, θ can be differentiated with respect to time.
Now, evaluate the second derivative at θ = 0.
We have,
d2x/dt2 = -R(dθ/dt)2
The term dθ/dt is usually called the angular velocity, which is the rate of change of the angle θ. It has units of radians/second.
For convenience we can set w ≡ dθ/dt.
Therefore,
d2x/dt2 = -Rw2
This is the well-known form for the centripetal acceleration equation.
Solution For Problem # 4
The reason you feel weightless is because there is no force pushing against you, since you are not in contact with anything. Gravity is pulling equally on all the particles in your body. This creates a sensation where no forces are acting on you and you feel weightless. It would be the same sensation as if you were floating in space.
Solution For Problem # 5
Centripetal acceleration is the acceleration an object experiences as it travels a certain velocity along an arc. The centripetal acceleration points towards the center of the arc.
Centrifugal force is the imaginary force an unrestrained object experiences as it moves around an arc. This force acts opposite to the direction of centripetal acceleration. For example, if a car makes a sharp right turn the passengers would tend to slide in their seats away from the center of the turn, towards the left (if they are not wearing their seat belts, that is). The passengers would feel as if they are experiencing a force. This is defined as centrifugal force.
Solution For Problem # 6
Power is the rate of energy being generated or consumed. For example, if an engine produces 1000 Watts of power (where Watts is Joules/second), then after an hour the total energy produced by the engine is 1000 Joules/second × 3600 seconds = 3,600,000 Joules.
Solution For Problem # 7
The answer is (a).
Since the collision is head on and each car is identical and traveling at the same speed, the force of impact experienced by each car is equal and opposite. This means that the impact is the same as hitting a solid wall at 100 km/h.
Solution For Problem # 8
When you swing a hammer you increase its kinetic energy, so that by the time it strikes the nail it imparts a large force which drives the nail into the wood.
The hammer is basically an energy reservoir to which you are adding energy during the course of the swing, and which is released all at once upon impact. This results in the impact force greatly exceeding the maximum force you can exert by just pushing on the nail.
Solution For Problem # 9
This can be solved using an energy method.
We can solve this by equating the potential energy of the bow to the kinetic energy of the arrow.
The bow can be treated as a type of spring. The potential energy of a spring is:
(1/2)kx2, where k is the stiffness and x is the amount the spring is stretched, or compressed.
Therefore, the potential energy PE of the bow is:
PE = (1/2)(200)(0.75)2 = 56.25 J
The kinetic energy of a particle is:
(1/2)mv2, where m is the mass and v is the velocity.
The arrow can be treated as a particle since it is not rotating upon release.
Therefore, the kinetic energy KE of the arrow is:
KE = (1/2)(0.05)v2
If we assume energy is conserved, then
PE = KE
Solving for the velocity of the arrow v we get
v = 47.4 m/s
Solution For Problem # 10
Static friction is greater than kinetic friction.
Static friction exists if the wheels keep rolling on the ice without locking up, resulting in maximum braking force. However, if the wheels lock up then kinetic friction takes over since there is relative slipping between wheel and ice. This reduces the braking force and the car takes longer to stop.
Anti-lock braking systems (ABS) on a vehicle prevent the wheels from locking up when the brakes are applied, thus minimizing the amount of time it takes for the vehicle to reach a complete stop. Also, by preventing the wheels from locking up you have greater control of the vehicle.
College and University Physics Questions (mostly first year level)
Density Problems
Energy Problems
Force Problems
Friction Problems
Inclined Plane Problems
Kinematics Problems
Kinetic Energy Problems
Mechanics Problems
Momentum Problems
Pulley Problems
Statics Problems
Thermodynamics Problems
Torque Problems
Extra Challenging Physics Questions
The 20 physics questions given below are both interesting and highly challenging. You will likely have to take some time to work through them. These questions go beyond the typical problems you can expect to find in a physics textbook. Some of these physics questions make use of different concepts, so (for the most part) there is no single formula or set of equations that you can use to solve them. These questions make use of concepts taught at the high school and college level (mostly first year).
It is recommended that you persist through these physics questions, even if you get stuck. It's not a race, so you can work through them at your own pace. The result is that you will be rewarded with a greater understanding of physics.
Problem # 1
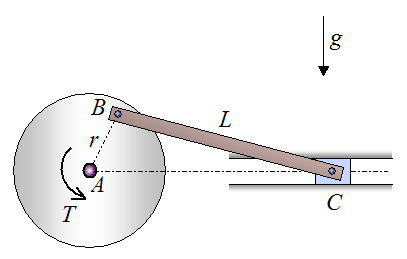
A crank drive mechanism is illustrated below. A uniform linkage BC of length L connects a flywheel of radius r (rotating about fixed point A) to a piston at C that slides back and forth in a hollow shaft. A variable torque T is applied to the flywheel such that it rotates at a constant angular velocity. Show that for one full rotation of the flywheel, energy is conserved for the entire system; consisting of flywheel, linkage, and piston (assuming no friction).
Note that gravity g is acting downwards, as shown.
Even though energy is conserved for the system, why is it a good idea to make the components of the drive mechanism as light as possible (with the exception of the flywheel)?
Problem # 2
An engine uses compression springs to open and close valves, using cams. Given a spring stiffness of 30,000 N/m, and a spring mass of 0.08 kg, what is the maximum engine speed to avoid “floating the valves”?
During the engine cycle the spring is compressed between 0.5 cm (valve fully closed) and 1.5 cm (valve fully open). Assume the camshaft rotates at the same speed as the engine.
Floating the valves occurs when the engine speed is high enough so that the spring begins to lose contact with the cam when the valve closes. In other words, the spring doesn’t extend quickly enough to maintain contact with the cam, when the valve closes.
For simplicity, you may assume that Hooke’s Law applies to the spring, where the force acting on the spring is proportional to its amount of compression (regardless of dynamic effects).
You may ignore gravity in the calculations.
Problem # 3
An object is traveling in a straight line. Its acceleration is given by
where C is a constant, n is a real number, and t is time.
Find the general equations for the position and velocity of the object as a function of time.
Problem # 4
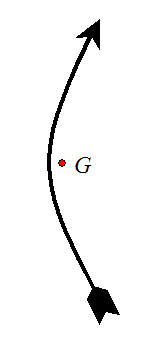
In archery, when an arrow is released it can oscillate during flight. If we know the location of the center of mass of the arrow (G) and the shape of the arrow at an instant as it oscillates (shown below), we can determine the location of the nodes. The nodes are the “stationary” points on the arrow as it oscillates.
Using a geometric argument (no equations), determine the location of the nodes.
Assume that the arrow oscillates in the horizontal plane, so that no external forces act on the arrow in the plane of oscillation.
Problem # 5
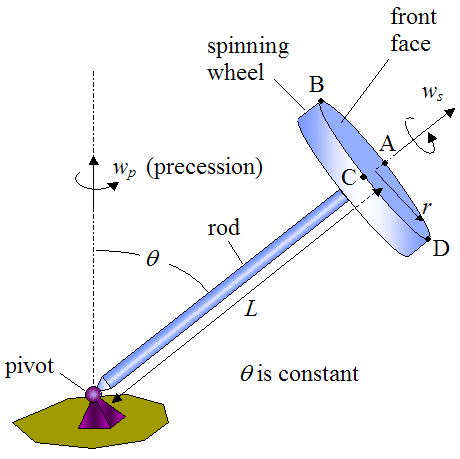
A gyroscope wheel is spinning at a constant angular velocity ws while precessing about a vertical axis at a constant angular velocity wp. The distance from the pivot to the center of the front face of the spinning gyroscope wheel is L, and the radius of the wheel is r. The rod connecting the pivot to the wheel makes a constant angle θ with the vertical.
Determine the acceleration components normal to the wheel, at points A, B, C, D labeled as shown.
Problem # 6
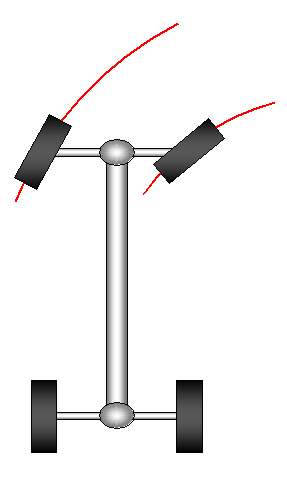
When a vehicle makes a turn, the two front wheels trace out two arcs as shown in the figure below. The wheel facing towards the inside of the turn has a steering angle that is greater than that of the outer wheel. This is necessary to ensure that both front wheels smoothly trace out two arcs, which have the same center, otherwise the front wheels will skid on the ground during the turn.
During a turn, do the rear wheels necessarily trace out the same arcs as the front wheels? Based on your answer, what are the implications for making a turn close to the curb?
Problem # 7
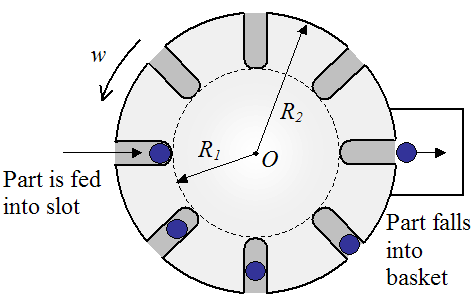
A horizontal turntable at an industrial plant is continuously fed parts into a slot (shown on the left). It then drops these parts into a basket (shown on the right). The turntable rotates 180° between these two stages. The turntable briefly stops at each 1/8th of a turn in order to receive a new part into the slot on the left.
If the rotational speed of the turntable is w radians/second, and the outer radius of the turntable is R2, what must be the inner radius R1 so that the parts fall out of the slot and into the basket, as shown?
Assume:
• The angular speed w of the turntable can be treated as constant and continuous; which means you can ignore the brief stops the turntable makes at each 1/8th of a turn.
• The location of the basket is 180° from the feed location.
• The slots are very well lubricated so that there is no friction between the slot and part.
• The parts can be treated as particles, which means you can ignore their dimensions in the calculation.
• The slots are aligned with the radial direction of the turntable.
Problem # 8
A flywheel for a single piston engine rotates at an average speed of 1500 RPM. During half a rotation the flywheel has to absorb 1000 J of energy. If the maximum permissible speed fluctuation is ± 60 RPM, what is the minimum rotational inertia of the flywheel? Assume there is no friction.
Problem # 9
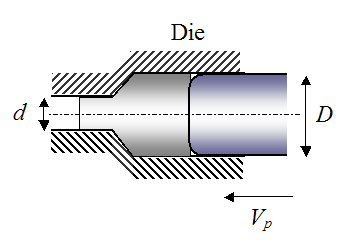
An aluminum extrusion process is simulated numerically with a computer. In this process, a punch pushes an aluminum billet of diameter D through a die of smaller diameter d. In the computer simulation, what is the maximum punch velocity Vp so that the net dynamic force (predicted by the simulation) acting on the aluminum during extrusion is at most 5% of the force due to deformation of the aluminum? Evaluate for a specific case where D = 0.10 m, d = 0.02 m, and the density of aluminum is ρ = 2700 kg/m3.
The force due to deformation of the aluminum during extrusion is given by
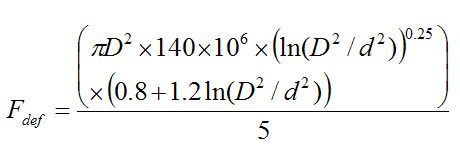
Hint:
The extrusion of the aluminum through the die is analogous to fluid flowing through a pipe which transitions from a larger diameter to a smaller diameter (e.g. water flowing through a fireman’s hose). The net dynamic force acting on the fluid is the net force required to accelerate the fluid, which occurs when the velocity of the fluid increases as it flows from the larger diameter section to the smaller diameter section (due to conservation of mass).
Problem # 10
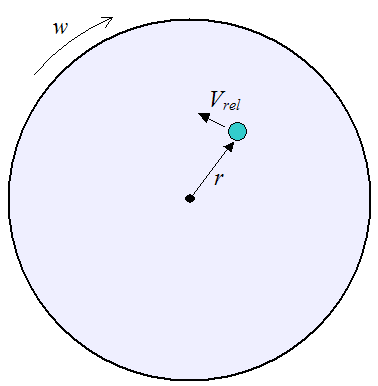
A child on a horizontal merry-go-round gives an initial velocity Vrel to a ball. Find the initial direction and velocity Vrel of the ball relative to the merry-go-round so that, relative to the child, the ball goes around in a perfect circle as he’s sitting on the merry-go-round. Assume there is no friction between merry-go-round and ball.
The merry-go-round is rotating at a constant angular velocity of w radians/second, and the ball is released at a radius r from the center of the merry-go-round.
Problem # 11
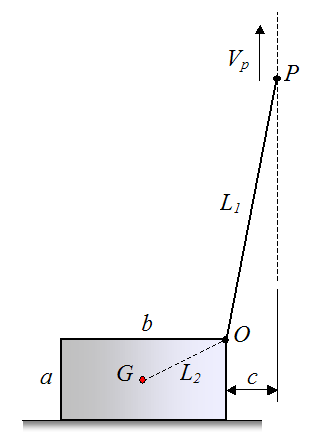
A heavy pump casing with a mass m is to be lifted off the ground using a crane. For simplicity, the motion is assumed to be two-dimensional, and the pump casing is represented by a rectangle having side dimensions ab (see figure). A cable of length L1 is attached to the crane (at point P) and the pump casing (at point O). The crane pulls up vertically on the cable with a constant velocity Vp.
The center of mass G of the pump casing is assumed to lie in the center of the rectangle. It is located at a distance L2 from point O. The right side of the pump casing is located at a horizontal distance c from the vertical line passing though point P.
Find the maximum cable tension during the lift, which includes the part of the lift before the pump casing loses contact with the ground, and after the pump casing loses contact with the ground (lift off). In this stage the pump casing swings back and forth.
Evaluate for a specific case where:
a = 0.4 m
b = 0.6 m
c = 0.2 m
L1 = 3 m
m = 200 kg
IG = 9 kg-m2 (rotational inertia of pump casing about G)
Assume:
• The friction between the pump casing and ground is high enough so that the pump casing does not slide along the ground (towards the right), before lift off occurs.
• Before lift off occurs, dynamic effects are negligible.
• The velocity Vp is fast enough so that the bottom of the pump casing swings clear of the ground after lift off occurs.
• For purposes of approximating the cable tension, you can model the system as a regular pendulum during swinging (you can ignore double pendulum effects).
• The mass of the cable can be neglected.
Problem # 12
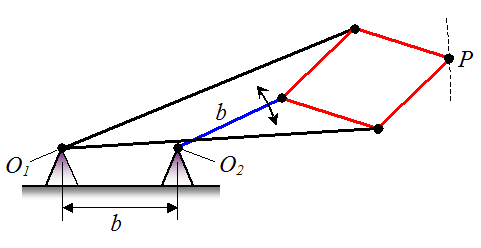
A linkage arrangement is shown below. The pin joints O1 and O2 are attached to a stationary base and are separated by a distance b. The linkages of identical color have the same length. All linkages are pin jointed and allow for rotation. Determine the path traced by the end point P as the blue linkage of length b rotates back and forth.
Why is this result interesting?
Problem # 13
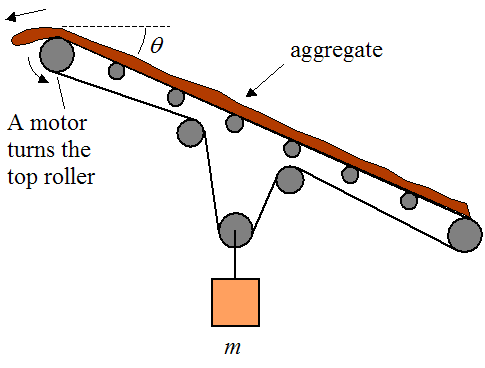
A conveyor belt carrying aggregate is illustrated in the figure below. A motor turns the top roller at a constant speed, and the remaining rollers are allowed to spin freely. The belt is inclined at an angle θ. To keep the belt in tension a weight of mass m is suspended from the belt, as shown.
Find the point of maximum tension in the belt. You don’t have to calculate it, just find the location and give a reason for it.
Problem # 14
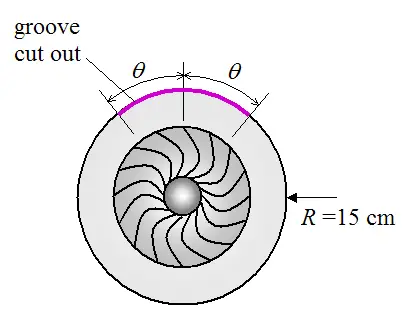
A quality test has determined that a pump impeller is too heavy on one side by an amount equal to 0.0045 kg-m. To correct this imbalance it is recommended to cut out a groove around the outer circumference of the impeller, using a milling machine, on the same side as the imbalance. This will remove material with the intent of correcting the imbalance. The dimension of the groove is 1 cm wide and 1 cm deep. The groove will be symmetric with respect to the heavy spot. How far around the outer circumference of the impeller should the groove be? Specify the answer in terms of θ. Hint: Treat the groove as a thin ring of material.
The outer radius of the impeller, at the location of the groove, is 15 cm.
The impeller material is steel, with a density of ρ = 7900 kg/m3.
Problem # 15
As part of a quality check, an axisymmetric container is placed over a very well lubricated fixed mandrel, as shown below. The container is then given an initial pure rotation w, with no initial translational motion. What do you expect to see if the center of mass of the container is offset from the geometric center O of the container?
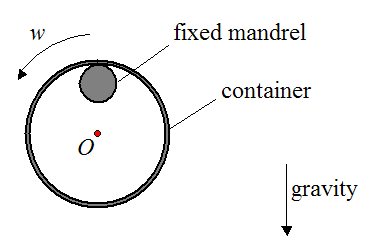
Problem # 16
A stream of falling material hits the plate of an impact weigher and the horizontal force sensor allows the mass flow rate to be calculated from this. If the speed of the material just before it strikes the plate is equal to the speed of the material just after it strikes the plate, determine an equation for the mass flow rate of the material, based on the horizontal force readout on the sensor. Ignore friction with the plate.
Hint: This can be treated as a fluid flow problem.
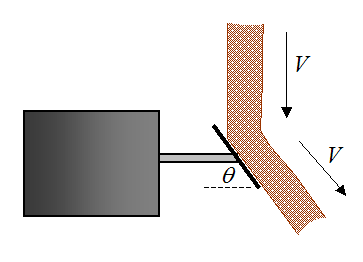
Problem # 17
The SunCatcher is a Stirling engine that is powered by solar energy. It uses large parabolic mirrors to focus sunlight onto a central receiver, which powers a Stirling engine. In the parabolic mirror you can see the reflection of the landscape. Why is the reflection upside down?

Source: http://www.stirlingenergy.com
Problem # 18
On a cold, dry winter day your glasses fog up when you go indoors after being outside for a while. Why is that?
And if you go back outside with your glasses still fogged up, they quickly clear up. Why is that?
Problem # 19
In an astronaut training exercise, an airplane at high altitude travels along a circular arc in order to simulate weightlessness for its passengers. Explain how this is possible.
Problem # 20
A rope is wrapped around a pole of radius R = 3 cm. If the tension on one end of the rope is T = 1000 N, and the coefficient of static friction between the rope and pole is μ = 0.2, what is the minimum number of times the rope must be wrapped around the pole so that it doesn’t slip off?
Assume that the minimum number of times the rope must be wrapped around the pole corresponds to a tension of 1 N on the other end of the rope.
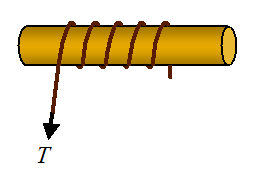
I created solutions for the 20 physics questions given above. The solutions are given in an ebook, in PDF format. They are available through this link.
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.