About me and why I created this physics website.

Friction Problems

On this page I put together a collection of friction problems to help you understand the concept of friction better. The required equations and background reading to solve these problems are given on the friction page and the equilibrium page.

Problem # 1

A block of mass M = 10 kg is sitting on a surface inclined at angle θ = 45°. Given that the coefficient of static friction is μ_s = 0.5 between block and surface, what is the minimum force F necessary to prevent slipping? What is the maximum force F that can be exerted without causing the block to slip?

Hint and answer




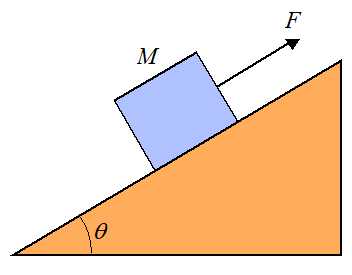
Problem # 2

In the previous problem use θ = 15°. What is the maximum force pushing down the incline so that the block doesn't slip? What is the maximum force pushing up the incline so that the block doesn't slip?

Hint and answer


Problem # 3

A conveyor is dumping sand onto a cone shaped pile. Given that the coefficient of static friction between the sand grains is μ_s, what is the maximum angle θ?

Hint and answer




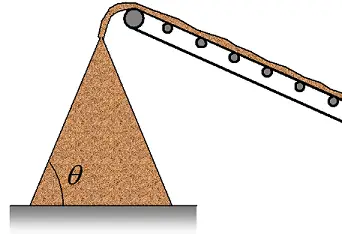
Problem # 4

A uniform ladder of length L is leaning against the side of a building, as shown. A person of mass m = 75 kg is standing on it. The mass of the ladder is M = 10 kg. The coefficient of static friction between the ground and ladder is μ_s1 = 0.5, and the coefficient of static friction between the wall and ladder is μ_s2 = 0.3. What is the minimum angle θ so that the ladder doesn't slip?

Hint and answer




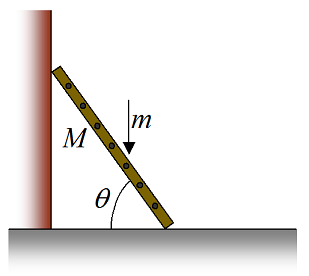
Problem # 5

Two boards are bolted together with two bolts, as shown. The squeeze force between the boards is 500 lbs. If the shear strength of each bolt is 5000 lbs and the coefficient of static friction between the boards is μ_s = 0.5, what is the maximum force F that can be applied to the boards and not pull them apart?

Hint and answer




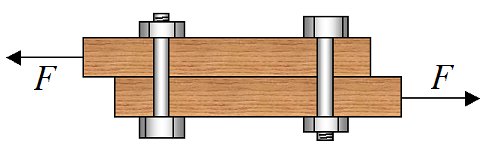
Problem # 6

A 50 kg crate is being pushed on a horizontal floor at constant velocity. Given that the coefficient of kinetic friction between crate and floor is μ_k = 0.1, what is the push force F? (Answer: 49 N)




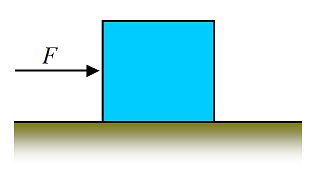
Problem # 7

In the previous problem we are given that the coefficient of static friction between crate and floor is μ_s = 0.2. What is the minimum force F to overcome friction with the floor? (Answer: 98 N)


Problem # 8

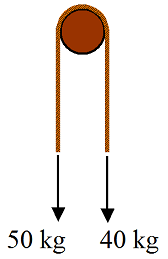
Two children throw a rope over a tree branch and hang off each end. The children have a mass of 40 kg and 50 kg. What is the minimum coefficient of static friction between rope and tree branch so that the rope doesn't slip? To solve this consider the general equation T₂ = T₁e^μθ, where T₁ and T₂ are the rope tensions on the two ends (with T₂ > T₁), μ is the coefficient of static friction between rope and tree branch, and θ is the angle of contact between rope and branch, in radians. For example, if the rope wraps completely around the branch then the angle θ = 2π.

Hint and answer




The hints and answers for these friction problems will be given next.

Hints And Answers For Friction Problems


Hint and answer for Problem # 1

The minimum force required to prevent slipping is the minimum force that will prevent the block from sliding down the incline. It is F_min = 10gsin(45°)−10gcos(45°)×0.5. The maximum force that can be exerted without causing the block to slip is the maximum force that can be exerted without causing the block to slide up the incline. It is F_max = 10gsin(45°)+10gcos(45°)×0.5.

Answer: F_min = 34.65 N, F_max = 103.94 N


Hint and answer for Problem # 2

The maximum force pushing down the incline is 10gcos(15°)×0.5−10gsin(15°). The maximum force pushing up the incline is 10gcos(15°)×0.5+10gsin(15°).

Answer: F_max = 21.97 N (pushing down the incline), F_max = 72.69 N (pushing up the incline)


Hint and answer for Problem # 3

The maximum sliding angle is θ. By analogy, we can analyze this as a block sitting on an incline which has friction. The force of gravity pulling down on the block is F₁ = Mgsinθ, where M is the mass of the block. The maximum friction force opposing the sliding is F₂ = Mgcosθμ_s. At some angle θ the block will be on the verge of sliding. This is the maximum angle θ and occurs when F₁ = F₂. The maximum angle θ can be solved from this.

Answer: θ_max = atan(μ_s)


Hint and answer for Problem # 4

This is a good static equilibrium problem. It is particularly interesting because almost everyone has stood on a ladder before, but little thought is usually given to the minimum angle to avoid slipping. It is something you just sense intuitively.

The minimum angle θ must correspond to the case where the person is standing at the very top of the ladder, since this produces a limiting condition where ladder slip is most likely.

Use the following sign convention: The upward and rightward direction is positive. The downward and leftward direction is negative. Counterclockwise rotation is positive. Clockwise rotation is negative.

Apply the condition of rotational equilibrium. Take the sum of the moments about the base of the ladder. This gives us: mgLcosθ+Mg(L/2)cosθ−N₂sinθL−F₂cosθL = 0, where N₂ is the (horizontal) normal force at the wall, F₂ is the (vertical) friction force at the wall, and L/2 (in the second term) corresponds to the midpoint of the ladder and is the point at which the gravitational force acts, since the ladder is uniform. Call this equation (1).

Apply the condition of horizontal equilibrium: N₂ = F₁, where F₁ is the (horizontal) friction force at the ground. Call this equation (2).

Apply the condition of vertical equilibrium: -Mg−mg+F₂+N₁ = 0, where N₁ is the (vertical) normal force at the ground. Call this equation (3).

The maximum allowable friction force at the wall is: F₂ = μ_s2N₂. Call this equation (4).

The maximum allowable friction force at the ground is: F₁ = μ_s1N₁. Call this equation (5).

Combine equations (1)-(5) to obtain an equation for θ. Note that the length of the ladder L cancels out. We have:

tanθ = (2m+M−Mμ_s1μ_s2)/(2μ_s1m+2μ_s1M). We can then substitute the known values to calculate θ, which is the minimum angle to prevent slipping.

Answer: θ_min = 61.8°


Hint and answer for Problem # 5

To pull the boards apart the friction force between the boards, plus the shear strength of the bolts, must be exceeded. Therefore the maximum pull force must be below the force needed to do this. Hence, F_max = 2×5000+500×0.5.

Answer: 10250 lbs


Hint and answer for Problem # 8

In the equation T₂ = T₁e^μθ, we have T₂ = 50 kg, T₁ = 40 kg, and θ = π. We can then solve for μ, and this is the minimum coefficient of static friction.

Answer: μ_min = 0.071

---

Bonus Problems Related to Friction

1. Are two interlaced phone books impossible to pull apart by any means?

2. Can you use a whip to swing safely across a chasm? (from Indiana Jones movie)

I created a physics analysis for these two problems, in PDF format. It's available through this link.



Return to Physics Questions page


Return to Real World Physics Problems home page