About me and why I created this physics website.

Momentum Problems

On this page I put together a collection of momentum problems to help you understand momentum better. The required equations and background reading to solve these problems is given on the momentum pages on the dynamics page.

Problem # 1

A particle has a mass of 10 kg and a velocity of 5 m/s. What is the momentum of the particle? (Answer: 50 kg·m/s)


Problem # 2

An impulse of 20 kg·m/s acts on the particle in problem # 1, in the same direction as the velocity. What is the final velocity of the particle? (Answer: 7 m/s)


Problem # 3

If the impulse in problem # 2 is delivered for a duration of 0.5 seconds, what is the average force acting on the particle? (Answer: 40 N)


Problem # 4

An elastic collision occurs in one dimension, in which a 10 kg block traveling at 5 m/s collides with a 5 kg block traveling at 3 m/s in the same direction. What are the velocities of the two blocks immediately after the collision? (Answer: 3.67 m/s, 5.67 m/s)


Problem # 5

An inelastic collision occurs in one dimension, in which a 10 kg block traveling at 5 m/s collides with a 5 kg block traveling at 3 m/s in the same direction, and they stick together. What are the velocities of the blocks immediately after the collision? (Answer: 4.33 m/s)


Problem # 6

A simple and practical understanding of conservation of momentum problems is given by the following: When a figure skater makes a jump, he increases his rotation speed by pulling together his arms and legs. This reduces his rotational inertia causing him to spin faster. If the initial spin rate of a figure skater is 1 RPM and he decreases his rotational inertia by half during the spin, what is his final spin rate? (Answer: 2 RPM)


Problem # 7

When two billiard balls collide the collision is assumed to be elastic. Show that for a general case, where the collision is not head on, the cue ball moves in a direction perpendicular to the direction of the object ball, after impact. Assume that the balls have the same mass and the object ball is initially at rest.

(For the answer see the physics of billiards page)


Problem # 8



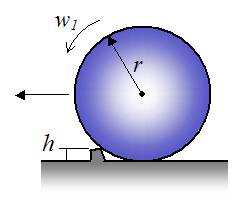
A solid ball of mass m and radius r is rolling without slipping on a flat horizontal surface, at an initial angular velocity w₁. It hits a small bump of height h. What is the angular velocity of the ball immediately after impact? Also, what is the minimum initial angular velocity w₁ so that the ball just makes it over the bump? What is the minimum initial speed of the ball?

Assume that the ball pivots about the tip of the bump during, and after impact.

(For the answer see the impulse and momentum page)


Problem # 9

In the angular momentum page we showed how the angular momentum equations for a rigid body are derived. The figure below shows the set up used for the derivation.



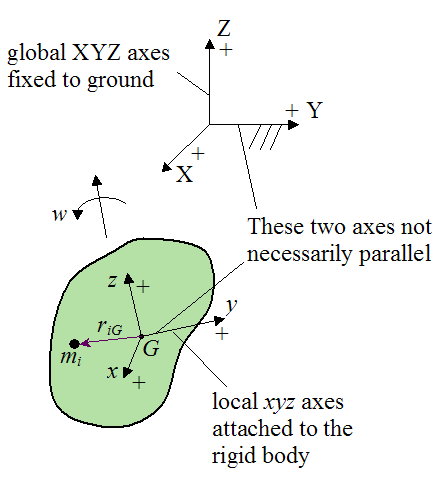
Where:

r_iG is the position vector from point G (the center of mass of the rigid body) to the location of m_i. This vector is measured relative to the local xyz axes

m_i is the mass of a small, arbitrary mass element in the rigid body. This mass element is small enough to be considered a particle

w is the angular velocity vector of the rigid body with respect to ground


Introduce the following new variables:

r_i is the position vector from the origin o of the global XYZ frame (ground) to particle i. This vector is measured relative to the local xyz axes

r_G is the position vector from point o to point G. This vector is measured relative to the local xyz axes

v_i is the velocity vector of particle i with respect to ground and with components resolved along the local xyz axes

v_G is the velocity vector of point G with respect to ground and with components resolved along the local xyz axes

v_iG is the velocity vector of this mass element relative to point G, and with components resolved along the local xyz axes


The following vector equation defines the angular momentum (H_oi) of an arbitrary particle i, about an arbitrary ground reference point o:

H_oi = r_i×m_iv_i     (where '×' represents the vector cross product)

If we set,

r_i = r_G+r_iG

and

v_i = v_G+v_iG

show that the angular momentum (H_o) of a rigid body about an arbitrary ground reference point o is given by:

H_o = ΣH_oi = mr_G×v_G+H_G

where m is the mass of the rigid body, Σ represents summation over all the particles in the rigid body, and H_G is the angular momentum of the rigid body about point G, as given by equation (6) on the angular momentum page. The above equation can be very useful when solving certain momentum problems, as shown in the next problem.


Problem # 10

See the problem, Cat righting reflex. This is an excellent real-world example to aid your understanding of conservation of momentum problems.

---

Bonus Problems Related to Momentum

1. Can a person be "blown away" by a bullet?

2. Can a watch-sized electromagnet deflect a bullet? (from James Bond movie)

3. Could a skydiver whose parachute failed to open hit a playground seesaw and send a small girl flying seven stories high, and she could still survive? (from urban myth)

I created a physics analysis for these three problems, in PDF format. It's available through this link.



Return to Physics Questions page


Return to Real World Physics Problems home page