About me and why I created this physics website.

Energy Problems

On this page I put together a collection of energy problems to help you understand energy better. The required equations and background reading to solve these problems are given on the conservation of energy page and the kinetic energy page.

Problem # 1

A solid ball of radius R rolls without slipping down a series of hills, as shown. Beyond the starting point, at what peak or valley is the kinetic energy of the ball minimized? Answer: The location is at peak h3

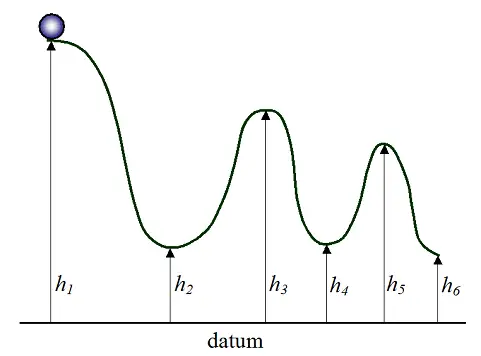
energy problems figure 1


Problem # 2

From the previous problem, find an equation for the speed of the ball at the determined location, assuming the ball starts rolling from rest.

Hint and answer


Problem # 3

A block of mass M is traveling on a horizontal frictionless surface at a velocity V, before colliding with a spring. The spring has a stiffness k. How much is the spring compressed? Answer: V(M/k)1/2

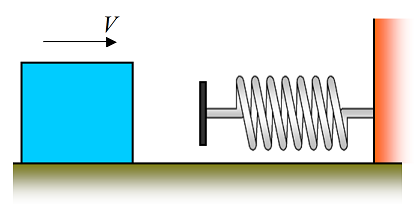
energy problems figure 2


Problem # 4

In the previous problem, the coefficient of kinetic friction is μk, between block and surface. How much is the spring compressed?

Hint and answer


Problem # 5

A block of mass M falls onto a spring. Before colliding with the spring the velocity of the block is V. The spring has a stiffness k. How much is the spring compressed? Answer: Mg/k+(1/k)[(Mg)2+MkV2]1/2

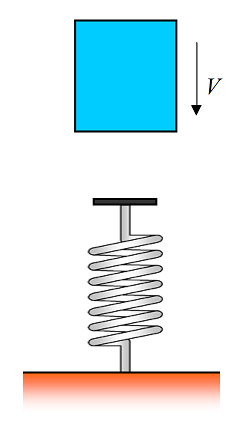
energy problems figure 3


Problem # 6

In the previous problem, 10% of the kinetic energy is lost during the collision between block and spring. How much is the spring compressed? Answer: Mg/k+(1/k)[(Mg)2+0.90×MkV2]1/2


Problem # 7

A block of mass M is traveling on a surface inclined at angle θ. The coefficient of kinetic friction is μk, between block and surface. The velocity of the block is V before colliding with a spring. The spring has a stiffness k. How much is the spring compressed?
Answer: -(Mgcosθμk−Mgsinθ)/k+(1/k)[(Mgcosθμk−Mgsinθ)2+MkV2]1/2

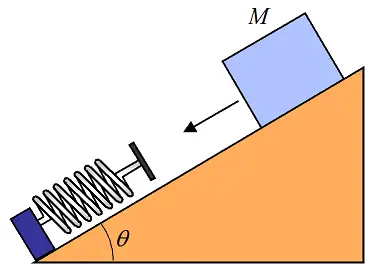
energy problems figure 4


Problem # 8

Two people are at the gym having a debate about how much energy is required to bench press a certain weight for one repetition. One person says that the energy required depends on how fast the weight is lifted. The other person says that it doesn't matter. Using an energy analysis determine which person is correct.

Hint and answer


The hints and answers for these energy problems will be given next.

Hints And Answers For Energy Problems


Hint and answer for Problem # 2

The kinetic energy of the ball consists of translational and rotational kinetic energy. Using conservation of energy we can solve for the speed of the ball. Therefore, mgh1 = mgh3+(1/2)m(VG)2+(1/2)IGw2, where m is the mass of the ball, VG is the velocity of the center of mass of the ball, w is the angular velocity of the ball, and IG is the rotational inertia of the ball about its center of mass. For no slipping w = (VG)/R, where R is the radius of the ball. And IG = (2/5)mR2. Combining these three equations we can solve for VG.

Answer: VG = [(10g/7)(h1−h3)]1/2


Hint and answer for Problem # 4

The friction force produces an additional energy term in the energy equation. The energy equation is (1/2)MV2 = (1/2)ks2+Mgμks, where Mg is the normal force, and s is the sliding distance, which is equal to the spring compression. This is a quadratic equation with two roots. We reject the negative root. The positive root is the solution.

Answer: s = -(Mgμk)/k+(1/k)[(Mgμk)2+MkV2]1/2


Hint and answer for Problem # 8

We can apply the principle of work and energy since it is very convenient for this type of problem. The corresponding equation to consider is: T1+W−mgL = T2, where W is the lift energy applied to the weight during the lift, m is the mass of the weight, L is the lift distance of the weight, T1 is the initial kinetic energy of the weight (at the start of the bench press), and T2 is the final kinetic energy of the weight (at the end of the bench press). Clearly, T1 = T2 = 0, since the starting and ending velocity of the weight is zero. We can then solve for W from the above equation.

Answer: W = mgL. This answer is interesting because it means that the total lift energy does not depend on how fast the weight is lifted.


Energy problems like the ones given above are a good way to test understanding. For interesting real-world problems see: Jump height on another planet and Kinetic energy of a bullet relative to the gun.



Return to Physics Questions page


Return to Real World Physics Problems home page