About me and why I created this physics website.

Thermodynamics Problems

On this page I put together a collection of thermodynamics problems to help you understand thermodynamics better. These problems are designed to help you understand some of the fundamentals without going into too much depth. Thermodynamics is somewhat of a strange subject which isn't always easy to connect to the real-world in the way that, say, dynamics theory is. This is why I chose problems which have at least some practical relevance.

Problem # 1

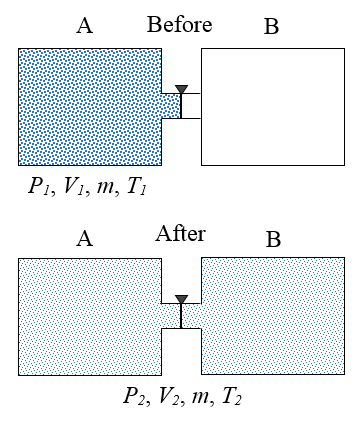
A gas is initially contained inside an insulated container A, at initial conditions P₁, V₁, m, and T₁. These quantities represent pressure, volume, mass, and temperature, respectively. A valve is then opened which allows the gas to expand freely into an insulated container B, which is initially empty. After the gas has settled, the final conditions of the gas are P₂, V₂, m, and T₂. In thermodynamics, a process is said to be reversible if it produces no entropy. This means that the process can happen in the reverse direction. Explain why the process described is not reversible.

See answer




Problem # 2

Air with a relative humidity of 30% at 20°C is pumped into a container. What is the maximum pressure inside the container so that water does not condense on the inside of the container? Assume the air temperature inside the container is 20°C.

See answer


Problem # 3

For all heat engines, the maximum work output (W) is related to the maximum heat input energy (Q) by the following equation:



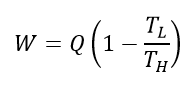
where T_H is the temperature of the heat source, and T_L is the temperature of the heat sink, which is the temperature of the "leftover" heat energy after work is extracted from the process. Both temperatures are in units of Kelvin.

The term inside the brackets represents the thermal efficiency of the process, commonly known as the Carnot efficiency.

In an application involving a Stirling engine (a type of heat engine, shown below), a parabolic dish is used to concentrate solar energy onto the receiver of the engine. Using the equation above, why would this produce more power output than using non-concentrated solar energy as the heat source, collected over the same area as the dish.

See answer



Source: http://www.stirlingenergy.com


Problem # 4

Steam at a temperature of 350°C and a pressure of 1 MPa is flowing through a pipe. What is the enthalpy of the steam?

See answer


Problem # 5

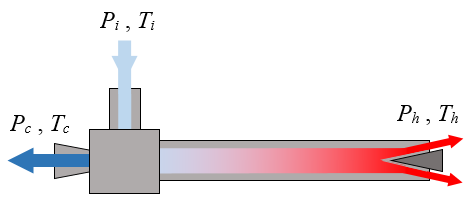
A vortex tube, also known as a Ranque-Hilsch vortex tube, is a mechanical device without moving parts that separates a compressed gas into hot and cold streams. According to a manufacturer's specifications, pressurized air enters a vortex tube at a temperature of 20°C and a guage pressure of 700 kPa. Cold air exits the left side of the tube at a temperature of -18°C and at atmospheric pressure. Hot air exits the right side of the tube at a temperature of 105°C and at atmospheric pressure. The ratio of mass flow rate between the cold stream and the inlet stream is 0.70. Are these specifications possible?

See answer




Problem # 6

An air-powered car is powered using high pressure compressed air stored in a tank. The pressurized tank is connected to an air-powered engine. The volume of the tank is 0.3 m³, and the initial temperature and pressure of air inside the tank is 20°C and 30 MPa, respectively. Using online resources, analyze the efficiency of the Air Car.

See answer


Problem # 7

A Drop Tower is a popular ride in amusement parks. To make the ride as energy efficient as possible, one can set up an electric motor and regenerative battery system in which energy from the battery is used to drive the electric motor to lift the riders to the top of the ride. As the riders descend down the ride, the "falling" energy is used to recharge the battery. Given that friction is unavoidably present, explain why this ride is an example of an irreversible process.

See answer



Source: https://commons.wikimedia.org/wiki/File:Freefall_moviepark.png


Problem # 8

It is theorized by scientists that advanced alien civilizations would use a large percentage of the energy of their parent star. This would result in a lot of waste heat being generated on an enormous scale, which has the potential of being detectable using telescopes here on earth. Explain how this theory makes sense from a thermodynamics sense, using our civilization as an example.

See answer


Answers For Thermodynamics Problems

Answer for Problem # 1

Since the containers are insulated, no heat transfer occurs between the gas and the external environment, and since the gas expands freely into container B there is no resistance "pushing" against it, which means no work is done on the gas as it expands. As a result, the internal energy of the gas remains the same, before and after the expansion. To return the gas to its original state, it would have to be compressed back into container A. This unavoidably takes place against a resistive pressure force (exerted by the gas), which means that work is required to do so. This would add energy to the gas, thereby increasing its internal energy, resulting in a temperature and pressure of the gas greater than its initial temperature and pressure (inside container A). It would then have to be cooled to bring it back to the conditions P₁ and T₁. This would add heat to the environment which would increase entropy. Hence, the gas cannot be returned to its initial state under the reverse conditions, and the process described in the problem is therefore not reversible.


Answer for Problem # 2

For air at atmospheric pressure and at a temperature of 20°C, containing water vapor such that the relative humidity is 30%, the partial pressure of the water vapor is P_w = 0.30×P_g (according to the definition of relative humidity), where P_g is the pressure of saturated water vapor. Referring to a thermodynamics table containing the properties of saturated water (H₂O), P_g = 0.002338 MPa. So, P_w = 0.30×0.002338 = 0.0007 MPa. We wish to calculate the air pressure inside the container so that P_w = P_g. This means that the partial pressure of the water vapor inside the container is equal to the pressure of saturated water vapor (at 20°C). If we increase the air pressure by some multiple M, then the partial pressure of the water vapor present in the air will increase by the same multiple M (based on Dalton's law of partial pressures). Therefore, M = 0.002338/0.0007 = 3.34. The maximum pressure inside the container is then 3.34×(atmospheric pressure) = 340 kPa, approximately, for atmospheric pressure = 101.3 kPa. At this pressure the water vapor will begin to condense inside the container (at the dew point temperature of 20°C). Note that having water condense inside the container can be undesirable given that it can cause corrosion or mold growth. This is prevented by keeping the pressure inside the container less than 340 kPa, so that water condensation doesn't occur.


Answer for Problem # 3

According to the equation for Carnot efficiency, a greater temperature difference between heat source and heat sink results in greater power output (higher thermal efficiency). And a lower temperature difference results in lower power output (lower thermal efficiency). This is why, for purposes of solar thermal power generation, it is desirable to focus sunlight from a large area onto a small area. The result is much higher temperature for the heat source and much higher thermal efficiency as a result, which means much higher power output for the engine. For example, a collector of surface area A that is collecting heat energy from the sun to run a heat engine, is much less efficient (and produces much less power) than a heat engine that uses that same energy, but in concentrated form. In other words, focusing the sunlight impinging on A onto a small point and using that energy to run a heat engine is much more efficient and produces more power than using unfocused sunlight falling on the collector. The more you can focus the heat energy the more power you will get. This is why Stirling dishes, which focus sunlight to a point, produce more power than parabolic troughs, which focus sunlight along a line (assuming both use the same area of sun exposure). The focal temperature is higher in the Stirling dishes than in parabolic troughs, which is why they are more efficient.


Answer for Problem # 4

This can be determined by looking directly at superheated steam tables. For the given temperature and pressure, the enthalphy is 3157.7 kJ/kg.


Answer for Problem # 5

Let m_i be the mass flow rate of the air at the inlet, m_c be the mass flow rate of the air at the cold outlet, and m_h be the mass flow rate of the air at the hot outlet.

First, check the First Law of Thermodynamics (which is an energy balance equation), assuming a steady state and adiabatic process in which there is negligible heat transfer to or from the air as it flows through the vortex tube, so we don't have to account for energy contribution due to heat transfer. This is a reasonable assumption since the air is flowing quickly through the vortex tube. In addition, there is no work energy added to or extracted from the vortex tube. We have

m_ih_i − (m_ch_c + m_hh_h) = 0

Where:

h_i is the enthalpy of the air at the inlet

h_c is the enthalpy of the air at the cold outlet

h_h is the enthalpy of the air at the hot outlet

Divide the above equation by m_i. We get

h_i − (m_c/m_i)h_c − (m_h/m_i)h_h = 0

Now, m_c/m_i = 0.70, and m_h/m_i = 0.30.

Referring to a thermodynamic table containing the enthalpy for air,

At 20°C and 801.3 kPa (700 kPa guage pressure), h_i = 293 kJ/kg

At -18°C and 101.3 kPa, h_c = 255 kJ/kg

At 105°C and 101.3 kPa, h_h = 379 kJ/kg

Substitute the values into the left side of the above equation and see if it is equal to 0. We get

293 − (0.70)(255) − (0.30)(379) = 0.8

This is not quite equal to 0, but it is within the range of round-off error.

The next step is to check the Second Law of Thermodynamics (which is an entropy production equation), assuming once more a steady state and adiabatic process in which there is no heat transfer to or from the air as it flows through the vortex tube, so we don't have to account for entropy production due to heat transfer. We have

S = (m_cs_c + m_hs_h) − m_is_i

Where:

S_i is the total entropy production

s_i is the entropy of the air at the inlet

s_c is the entropy of the air at the cold outlet

s_h is the entropy of the air at the hot outlet

Divide the above equation by m_i. We get

S/m_i = (m_c/m_i)s_c + (m_h/m_i)s_h − s_i

Referring to a thermodynamic table containing the entropy for air,

At 20°C and 801.3 kPa (700 kPa guage pressure), s_i = 6.3 kJ/(kg·K)

At -18°C and 101.3 kPa, s_c = 6.7 kJ/(kg·K)

At 105°C and 101.3 kPa, s_h = 7.1 kJ/(kg·K)

Substitute the values into the right side of the above equation and see if it is greater than 0. This would mean that the process produces entropy and is physically possible from a thermodynamics sense. We get

(0.70)(6.7) + (0.30)(7.1) − 6.3 = 0.52

This is greater than 0. So based on the first and second law of thermodynamics, the process is physically feasible. But this does not, however, tell you that it's possible from a technological sense, the same way that Carnot efficiency for a heat engine only tells you what's theoretically possible subject to the restrictions of thermodynamics. It does not tell you what's possible based on other restrictions, such as from technological limitations. Also, this analysis does not tell you how the vortex tube works, which is a whole other discussion, quite complicated in fact.


Answer for Problem # 6

Using thermodynamics we can estimate the efficiency of the air car, as follows:

The efficiency of the air car is equal to 100×(output energy)/(input energy). The input energy is equal to the amount of energy required to fill the tank with compressed air. Let's assume an ideal isothermal (constant temperature) process where the pressurized air being pumped into the tank is kept as close as possible to the ambient air temperature. This minimizes the pumping energy required to pump the air into the tank. This is achieved by cooling the pressurized air before it enters the tank. If the air is not simultaneously cooled as it is pumped into the tank it will reach a very high temperature, which will require a greater pumping energy than cooler air. Air heating up due to compression is a fundamental property of gases (which can be modeled here as an ideal gas, where PV = mRT). If you compress air into a smaller volume, it will tend to heat up.

It is important to mention, however, that (in the absence of air cooling) the extra input (pumping) energy would result in extra output energy as you drive the car, but only if the heated air in the tank could maintain its temperature. But in reality, the heated air would cool down to the ambient temperature. And that extra pumping energy would be for nothing (i.e. it wouldn't be recovered in the driving phase). So this is one reason why we have to cool the air as close as possible (within practical limits) to ambient temperature, as it enters the tank. This is achieved with multi-stage cooling.

With isothermal pumping of the air into the tank, the (ideal) input energy is, E_in = P₁V₁ln(P₂/P₁), where P₁ and V₁ is the initial (atmospheric) pressure and initial volume of the air, respectively, and P₂ is the pressure of the air after it's pumped into the tank. From the ideal gas equation given above, and given an isothermal process, P₁V₁ = P₂V₂, where V₂ is the volume of the tank. We can then calculate V₁ = 90 m³.

Substituting P₁ = 0.1 MPa (atmospheric pressure), P₂ = 30 MPa, and V₁ = 90 m³ into the equation above we calculate E_in = 51.3 MJ (megajoules).

Now, in reality the air heats up somewhat between cooling stages so this "forces" the compressor to use more than 51.3 MJ to pump air into the tank. Based on data from the European Fuel Cell Forum, a realistic efficiency factor for multi-stage cooling is 48% (ref: http://www.efcf.com/reports/E14.pdf). So the actual input energy is E_in = 51.3/0.48 = 107 MJ.

Once in the tank, the air will cool until its temperature reaches the ambient outdoor temperature. The energy of the air at this point will be 51.3 MJ.

Note that 51.3 MJ is greater than the actual energy that will be extracted from the tank to power the car. This is due to thermodynamic (physical) losses (a form of thermodynamic irreversibility). To keep these losses as low as possible it is necessary that the air is heated up as it expands inside the engine, after exiting the tank. Since air has a tendency to cool down upon expanding it is best to keep its temperature as high as possible using the ambient air as a heating source. In other words, we wish to maintain the (expanding) air temperature as close as possible to its temperature inside the tank. If this could be accomplished perfectly then the extracted energy will exactly equal 51.3 MJ. But in reality this is not the case. The air will unavoidably cool, so to help counteract this, multi-stage heating is used to heat the expanding air as it exits the tank and goes into the engine.

Based on data from the European Fuel Cell Forum, a realistic efficiency factor for multi-stage heating is 84% (ref: http://www.efcf.com/reports/E14.pdf). So the actual output energy is E_out = 51.3×0.84 = 43 MJ.

Therefore, the thermodynamic efficiency of the Air Car is 100×(E_out/E_in) = 40%.


Answer for Problem # 7

A process that produces no entropy is a reversible process because it can also be made to happen in the reverse direction. In this case the forward direction of the process is the ride being raised (which lowers the charge in the battery), and the reverse direction is the ride going back down (which increases the charge in the battery). The charge cannot be fully returned to the battery after the ride is completed because the friction present in the ride transforms part of the battery energy into heat energy which is lost to the environment (which produces entropy), and this cannot be recovered. Therefore the ride (on the way up or on the way down) is not a reversible process.


Answer for Problem # 8

If aliens somewhere in the universe are using a significant portion of a star's energy to power their civilization, a very large amount of waste heat would be produced as a result, which would lie in the mid-infrared portion of the electromagnetic spectrum. This is an inescapable consequence of the laws of thermodynamics. Energy cannot be destroyed, it can only change forms, and the common form of energy after being used is to end up as waste heat. Take a car for example; most of the energy of the fuel is lost as heat, and the remaining energy is used to move the car (i.e. perform useful work). However, to move the car, friction with the road and air must be overcome, along with internal friction of the engine and other moving parts in the car. Ultimately, this ends up as wasted heat as well. So essentially all the energy of the car's fuel ends up as waste heat. You can argue the same principle would apply for aliens using a large fraction of star energy. That energy is used to "do something", and after that task, or tasks, are performed, and assuming none of the energy is stored anywhere, that energy will end up as waste heat in the mid-infrared. You can go much deeper than this to explain the precise reasons why, but it's a basic consequence of the laws of thermodynamics.



Return to Physics Questions page


Return to Real World Physics Problems home page