About me and why I created this physics website.

Conservation Of Energy

Definition Of Conservation Of Energy

If a particle or body is acted upon only by conservative forces energy is conserved. This means that the total kinetic and potential energy in the system remains constant, and does not change. Such a system has no friction forces acting on it, and as such is an idealized simplification for solving problems using energy calculations.

Common examples of conservative forces acting on a particle or body are gravitational forces and (elastic) spring forces.

Conservation Of Energy For A Particle

Work Done By Gravity

Suppose a particle follows an arbitrary path, represented by the blue curve below.

The gravitational force acting on the particle is pointing down.

The arbitrary path traveled by the particle may be due to the presence of other forces also acting on the particle, but we do not need to consider them, since the work done by gravity is unaffected by them and can therefore be treated independently.




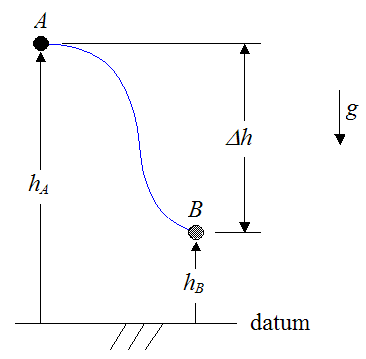
If Δh is equal to the final vertical position (at point B) minus the initial vertical position (at point A) then the work (W_g) done by gravity on the particle is given by the following scalar equation:



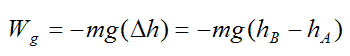
where m is the mass of the particle, and g is the acceleration due to gravity.

A negative sign is present in the above equation because vertical displacement (Δh) acting in the same direction as gravity (Δh < 0) must yield positive work, and vertical displacement acting in the opposite direction of gravity (Δh > 0) must yield negative work. So, if B is lower than A we have Δh < 0, and the negative sign accounts for this, making the work positive. On the other hand, if B is higher than A we have Δh > 0, and the negative sign accounts for this, making the work negative.

The expression for W_g is useful because no matter how complicated the path from A to B is, we only need to know the change in vertical height W_g and we can find the work done on the particle by gravity.


Work Done By An Elastic Spring

Consider a spring force acting on a particle, as shown below. The spring is attached to a wall at point O, where it can pivot. At position A of the particle, the spring is stretched or compressed by an amount s_A from its equilibrium (unstretched) position. At position B of the particle, the spring is stretched or compressed by an amount s_B from its equilibrium position. The arbitrary path traveled by the particle from A to B is represented by the blue curve.

Note that the dashed line represents the equilibrium position of the spring, where the spring is unstretched. Once again, the possible presence of other forces acting on the particle is irrelevant to this discussion, since we are only focusing on the work done by the spring.




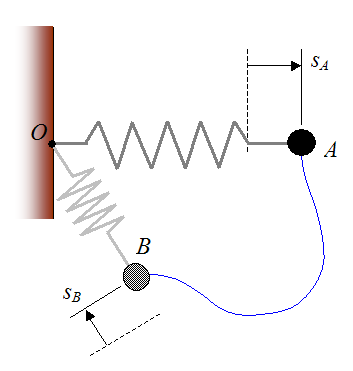
The work done by the spring (W_s) on the particle as it moves from A to B is given by the following scalar equation:



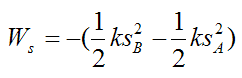
where k is the spring constant.

For the above equation we are assuming we have a spring that obeys Hooke's Law.

Therefore, the work done by the spring depends only on the position of A and B (relative to the position of point O), since this is what determines the amount of stretch or compression in the spring (s_A and s_B).


Principle Of Work And Energy

The (total) work done on the particle by the various forces (conservative and non conservative) as it moves from position A to position B is given by the general scalar equation:



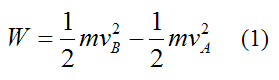
Where:

W is the (total) work done on the particle by the various forces

m is the mass of the particle

v_A is the velocity of the particle at position A, relative to an inertial reference frame (ground)

v_B is the velocity of the particle at position B, relative to an inertial reference frame (ground)

The right side of the above equation represents the change in kinetic energy of the particle between A and B.


If an elastic spring force and gravity force are acting on the particle, we can write:



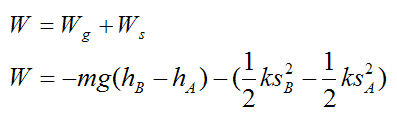
Substituting this equation into equation (1) we get



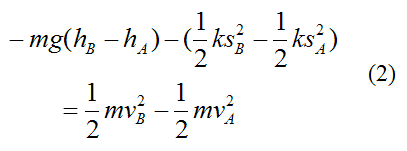
This can be rewritten as



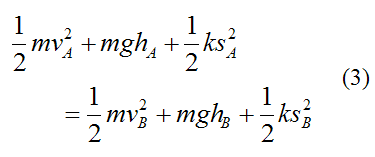
This equation tells us that the sum of the kinetic energy (1/2mv²), gravitational potential energy (mgh), and spring potential energy (1/2ks²) is always constant. Thus, there is conservation of energy in the system, regardless of the position of the particle.


Conservation of Energy

Equation (3) can be generalized as follows:



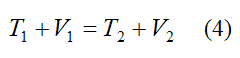
Where:

T₁ is the initial kinetic energy of the particle

V₁ is the initial potential energy associated with the conservative forces acting on the particle

T₂ is the final kinetic energy of the particle

V₂ is the final potential energy associated with the conservative forces acting on the particle


We define the potential energy for gravity as:



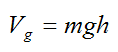
where the height h is measured from an arbitrary datum.


We define the potential energy for an elastic spring as:



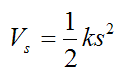
where s is the amount that the spring is stretched or compressed from its unstretched position.


One can make a choice whether to use the general equation (1) (which applies whether or not there is conservation of energy in the system), or equation (4) which applies only when there is conservation of energy in the system.

Equation (4) can also be applied to a system of particles that are only subjected to conservative forces. As a result we can write:



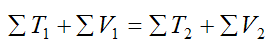
This equation tells us that the sum of the initial kinetic and potential energy in the system of particles is equal to the sum of the final kinetic and potential energy in the system of particles.


Conservation Of Energy For A Rigid Body

Work Done By Gravity

If we have a rigid body instead of a particle, the same basic analysis applies. We simply treat the center of mass of the rigid body as a particle, and apply the above procedure to find the work done by gravity. In other words, if we want to find the work done by gravity on the rigid body we look at the motion of its center of mass, and then apply the equation above for W_g. This is shown below. The red dot represents the center of mass of the rigid body. The mass of the rigid body is m. The acceleration due to gravity is g.

Suppose the center of mass of a rigid body follows an arbitrary path, represented by the blue curve below.




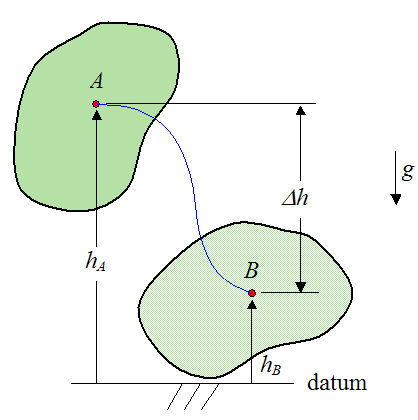
The work done by gravity on the rigid body is dependent only on the change in vertical height Δh of the center of mass of the rigid body, as it moves from A to B.

If Δh is equal to the final vertical position (at point B) of the center of mass minus the initial vertical position (at point A) of the center of mass, then the work (W_g) done by gravity on the rigid body is given by the following scalar equation:



Note that it doesn’t matter at all how the rigid body moves. We only need to know the vertical displacement of its center of mass (as it moves from A to B) to determine the work done by gravity.


Work Done By An Elastic Spring

If we replace the particle used in the previous case with a point on a rigid body (to which the end of the spring is attached), the work done by the spring on the rigid body is the same as for the work done on the particle (in the previous case). The figure below illustrates this situation.




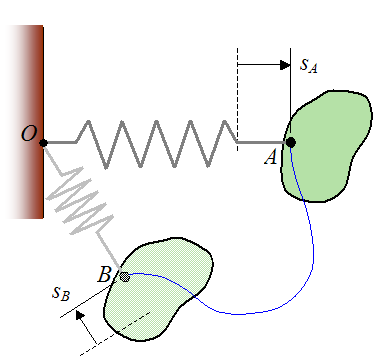
The work done by the spring on the rigid body is dependent only on the amount the spring is stretched or compressed from its equilibrium (unstretched) position, as it moves from A to B.

The work done by the spring (W_s) on the rigid body is given by the following scalar equation:



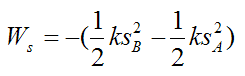
where k is the spring constant.

For the above equation we are assuming we have a spring that obeys Hooke's Law.

Note that it doesn’t matter at all how the rigid body moves. We only need to know the amount the spring is stretched or compressed from its equilibrium position (as it moves from A to B) to determine the work done by the spring.


Principle Of Work And Energy

The (total) work done on the rigid body by the various forces (conservative and non conservative) as it moves from position A to position B is given by the general scalar equation:



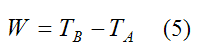
where T_A is the kinetic energy of the rigid body at position A, and T_B is the kinetic energy of the rigid body at position B.

Now,



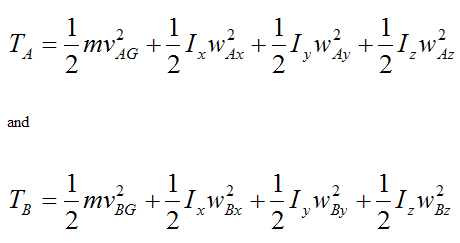
where the variables in T_A and T_B are defined on the page on kinetic energy. Note that T_A and T_B are the most general equations for three-dimensional rigid body motion.

If an elastic spring force and gravity force are acting on the rigid body, we can write:



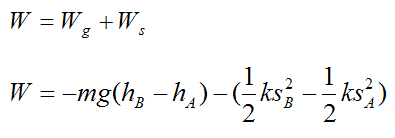
Substituting this equation into equation (5) we get



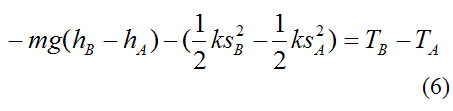
This can be rewritten as



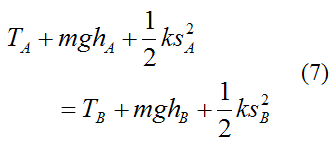
This equation tells us that the sum of the kinetic energy (T), gravitational potential energy (mgh), and spring potential energy (1/2ks²) is always constant. Thus, there is conservation of energy in the system, regardless of the position of the rigid body.


Conservation of Energy

Equation (7) can be generalized as follows:



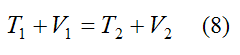
Where:

T₁ is the initial kinetic energy of the rigid body

V₁ is the initial potential energy associated with the conservative forces acting on the rigid body

T₂ is the final kinetic energy of the rigid body

V₂ is the final potential energy associated with the conservative forces acting on the rigid body


We define the potential energy for gravity as:



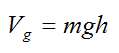
where the height h is measured from an arbitrary datum.


We define the potential energy for an elastic spring as:



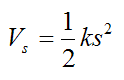
where s is the amount that the spring is stretched or compressed from its unstretched position.


One can make a choice whether to use the general equation (5) (which applies whether or not there is conservation of energy in the system), or equation (8) which applies only when there is conservation of energy in the system.

Equation (8) also applies to a system of rigid bodies that are only subjected to conservative forces (meaning there is conservation of energy in the system). For example, frictionless pins or inextensible cords may connect the bodies. Consequently, the forces acting at the points of contact between the bodies contribute zero work. The reason for this is because these forces are equal and opposite on each pair of contacting bodies (Newton’s Third Law), and move through the same distance. Therefore they cancel out, and contribute zero work to the system.


Example Problem For Conservation Of Energy

The figure below shows a general pendulum, in which an arbitrary rigid body is swinging back and forth in a plane, about a pivot P. Gravity is acting down and an elastic spring of stiffness k is attached to the body (at pivot point O) and to another pivot (Q), as shown. At the initial position shown, the spring is stretched by an amount s₁, as measured from its equilibrium (unstretched) length. When the pendulum is at its lowest position, the spring is compressed by an amount s₂ from its equilibrium (unstretched) length. If the pendulum has an angular velocity w₁ at the initial position shown, determine the angular velocity of the pendulum when it is at its lowest position. Ignore friction.




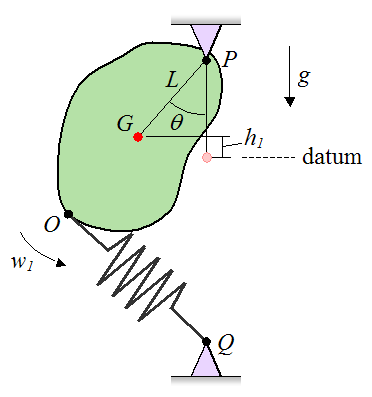
Additional variables are defined as follows:

w₂ is the angular velocity of the pendulum at its lowest position

G is the location of the center of mass of the rigid body

L is the distance from point P to point G

θ is the angle between the vertical and the line joining points P and G, at the initial position

h₁ is the height of point G, measured from the datum which is chosen as the lowest point of the swing, as shown

g is the acceleration due to gravity


By geometry,



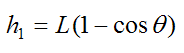
Since we are ignoring friction, the only forces acting on the pendulum are gravity and an (elastic) spring force. These forces are conservative, therefore we have conservation of energy in the system and we can apply equation (8):




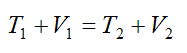
Since P is a fixed point on the pendulum (treated as a rigid body) we can apply the following kinetic energy equation (T₁) for planar motion, for the pendulum at the initial position:



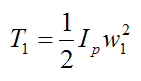
where I_p is the moment of inertia of the pendulum about an axis passing through point P (this axis is perpendicular to the plane of motion, so that it points out of the page).

Similarly, for the lowest part of the swing:




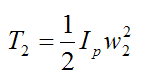
The potential energy at the initial position is equal to the sum of the gravitational potential energy and the spring potential energy:



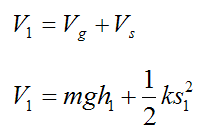
Similarly, for the lowest part of the swing:



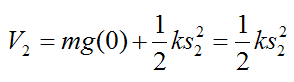
Thus we can write the following equation for conservation of energy of the pendulum:



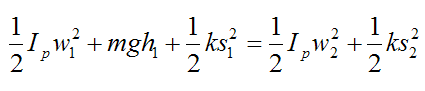
From this equation we can solve for w₂:



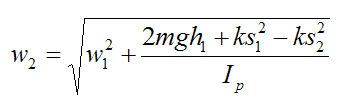
This is the angular velocity of the pendulum at the lowest point in the swing.



Return to Dynamics page


Return to Real World Physics Problems home page