About me and why I created this physics website.

Kinetic Energy

Kinetic Energy For A Particle

The kinetic energy for a particle is given by the following scalar equation:



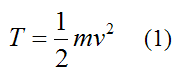
Where:

T is the kinetic energy of the particle with respect to ground (an inertial reference frame)

m is the mass of the particle

v is the velocity of the particle, with respect to ground


Kinetic Energy For A Rigid Body

Planar Motion

For a rigid body experiencing planar (two-dimensional) motion, the kinetic energy is given by the following general scalar equation:



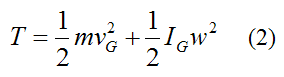
Where:

T is the kinetic energy of the rigid body with respect to ground

m is the mass of the rigid body

v_G is the velocity of the center of mass G of the rigid body, with respect to ground

I_G is the moment of inertia of the rigid body about an axis passing through the center of mass G, and perpendicular to the plane of motion

w is the angular velocity of the rigid body, with respect to ground


The figure below illustrates the general case where a rigid body is experiencing planar (two-dimensional) motion.




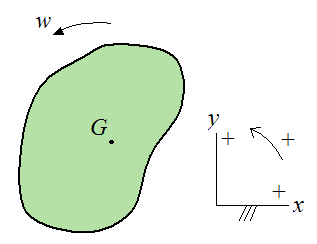
Note in equation (2) that the kinetic energy of the rigid body consists of two parts: The kinetic energy due to the velocity of the center of mass, and the kinetic energy due to rotation.


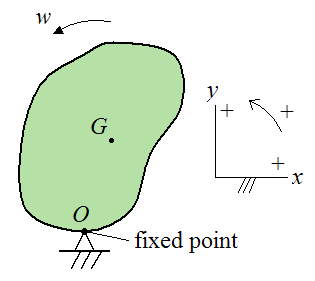
If the rigid body is rotating about a fixed point O that is attached to ground, we can express the kinetic energy as:



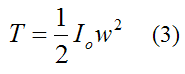
Where:

I_o is the moment of inertia of the rigid body about an axis passing through the fixed point O, and perpendicular to the plane of motion

w is the angular velocity of the rigid body, with respect to ground


The figure below illustrates the case where a rigid body is experiencing planar (two-dimensional) motion, and is rotating about a fixed point O.





Three Dimensional Motion

For general three-dimensional motion, the kinetic energy of a rigid body is given by the following general scalar equation:



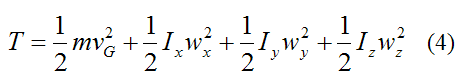
Where:

T is the kinetic energy of the rigid body with respect to ground

m is the mass of the rigid body

v_G is the velocity of the center of mass G of the rigid body, with respect to ground

w_x, w_y, w_z are the components of the angular velocity of the rigid body with respect to ground, and resolved along the local xyz axes (see figure below). To calculate these components, one must first determine the angular velocity vector of the rigid body with respect to the global XYZ axes, and then resolve this vector along the x, y, z directions to find the components w_x, w_y, w_z. This is often done using trigonometry.

I_x is the moment of inertia of the rigid body about the local x-axis, passing through the center of mass G (see figure below)

I_y is the moment of inertia of the rigid body about the local y-axis, passing through the center of mass G (see figure below)

I_z is the moment of inertia of the rigid body about the local z-axis, passing through the center of mass G (see figure below)


The moments of inertia I_x, I_y, I_z are the principal moments of inertia. This means that the local xyz axis is oriented such that the products of inertia I_xy, I_yz, I_zx all equal zero. For every rigid body, principal directions of inertia exist (where I_x, I_y, I_z are the principal moments of inertia). If a body has two or three planes of symmetry, the principal directions of inertia will be aligned with these planes.


The moment of inertia terms are given by



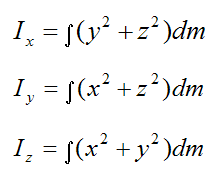
The product of inertia terms are given by




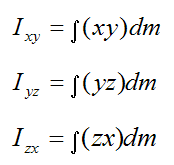
Note that for equation (4) the local xyz axes has its origin at the center of mass G of the rigid body.

Also note in equation (4) that the kinetic energy of the rigid body consists of two parts: The kinetic energy due to the velocity of the center of mass, and the kinetic energy due to rotation.





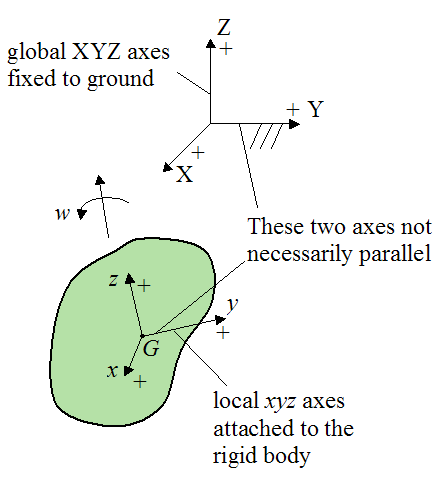
If the rigid body has a fixed point O that is attached to ground, we can give an alternate scalar equation for the kinetic energy of the rigid body:



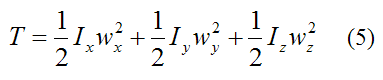
The variables are the same here as for equation (4). The only difference is that the local xyz axes has its origin at the fixed point O on the rigid body (instead of point G), as shown below. This means that the moment of inertia terms are calculated relative to point O (instead of point G).





Note that in equations (2)-(5), if we assume that the rigid body has negligible dimensions (where the inertia terms are close to zero), then the equations reduce to the kinetic energy equation for a particle – equation (1).

The scalar equations (2)-(5) can be used when solving problems involving energy calculations. For planar (two-dimensional) motion use equation (2) or (3). For general three-dimensional motion use equation (4) or (5).



Derivation of the kinetic energy equations for a rigid body (optional section)

The equations for planar (two-dimensional) motion follow naturally from the equations for general three-dimensional motion, so it is only necessary to derive the kinetic energy equations for three-dimensional motion.

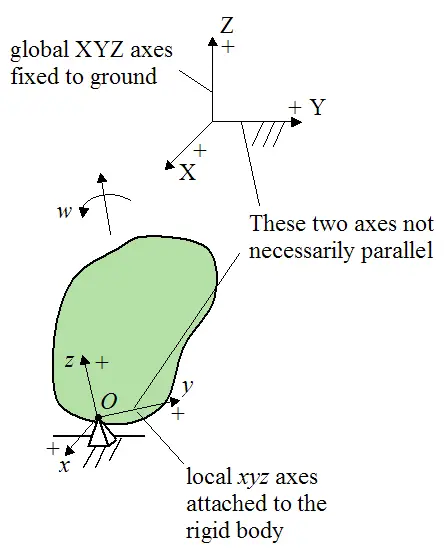
To derive the previous expressions for the kinetic energy of a rigid body we must apply the equation for kinetic energy of a small mass element in the rigid body, and then sum it over the entire rigid body. This problem is set up as shown in the figure below.




For a small mass element m_i in the rigid body the kinetic energy is given by the following scalar equation:



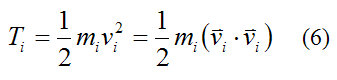
Where:

T_i is the kinetic energy of the small mass element, with respect to ground

m_i is the mass of the small mass element in the rigid body. This mass element is small enough to be considered a particle

v_i is the velocity vector of this small mass element with respect to ground, and resolved along the local xyz axes. To calculate this velocity, one must first determine the velocity vector v_i with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.


Now, from the equations for general motion of a rigid body:



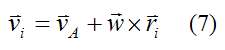
Where:

v_A is the velocity of point A with respect to ground, and resolved along the local xyz axes. To calculate v_A, one must first determine v_A with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.

w is the angular velocity of the rigid body with respect to ground, and resolved along the local xyz axes. To calculate w, one must first determine w with respect to the global XYZ axes, and then resolve this vector along the local xyz axes. This is often done using trigonometry.

r_i is the position vector from point A to the location of m_i. This vector is measured relative to the local xyz axes.


Substituting equation (7) into equation (6) we get



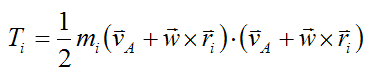
It remains to carry out the vector dot product followed by vector cross product multiplications and then sum T_i over the entire rigid body, using integration. Upon doing so we arrive at equation (4) for the case where point A coincides with the center of mass G. And we arrive at equation (5) for the case where point A coincides with a fixed point O on the rigid body. The full derivation is not shown here, since it is mostly a mathematical exercise, similar to the derivation of the Euler equations.



Return to Dynamics page


Return to Real World Physics Problems home page