The Physics Of Billiards

Source: http://www.flickr.com/photos/ventsislav/2222807833
Physics Of Billiards – Ball Collision
The physics behind billiards (or the physics behind pool), in large part, involves collisions between billiard balls. When two billiard balls collide the collision is nearly elastic. An elastic collision is one in which the kinetic energy of the system is conserved before and after impact. Therefore, for simplicity one can assume that for collisions involving billiard balls, the collision is perfectly elastic.
For collisions between balls, momentum is always conserved (just like in any other collision). For a simplified case assuming no friction (discussed below), we can combine this fact with the elastic-collision assumption to find the trajectory of two colliding billiard balls after impact. The figure below shows a collision between two billiard balls. For the general case, the collision is not head on, which is what the figure shows.
It is assumed that balls A and B have the same mass and that ball B is initially at rest (zero velocity). The initial velocity of ball A is V1A. After impact, ball A moves at velocity V2A in the direction shown, and ball B moves at velocity V2B in the direction shown.
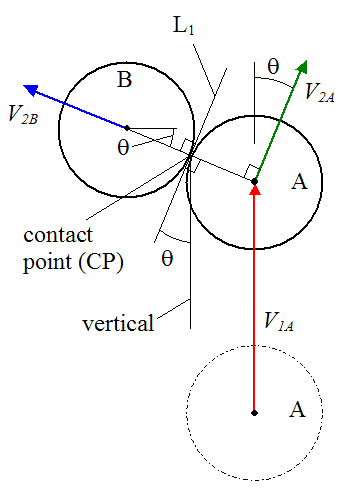
The line L1 is drawn at a tangent to both balls at the point of contact. Due to geometry, L1 is perpendicular to the line passing through the center of the two balls and the contact point CP. Due to geometry, L1 also makes an angle θ with the vertical, and the line passing through the center of the balls makes an angle θ with the horizontal.
After impact at CP, ball B moves in the direction of the line joining the center of the two balls, as shown. This is because the force (impulse) delivered by ball A to ball B acts normal to the surface of ball B, assuming there is no friction between the balls (a good assumption since billiard balls are smooth). Thus, ball B moves in the direction of this impulse.
Notice that, after impact, ball A moves in a direction perpendicular to the direction of ball B. This interesting result can be proven as follows.
Analysis Of Ball Collision
For the two colliding balls, the general vector equation for conservation of linear momentum is:
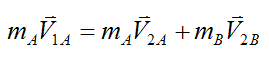
Since the masses mA and mB are assumed equal, this equation simplifies to:
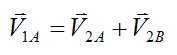
For an elastic collision kinetic energy is conserved, and the equation is:
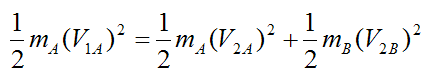
Since the masses mA and mB are equal, this equation simplifies to:
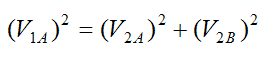
By the Pythagorean theorem, this last equation tells us that the vectors V1A, V2A, V2B form a right-angled triangle. Therefore, the vector equation for conservation of momentum can be drawn as shown below.
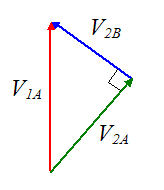
Thus, after impact ball A moves in a direction perpendicular to the direction of ball B. This is a very slick result.
There are two additional special cases to consider, involving ball collision.
For the case where the target ball B must be hit at an angle θ very close to zero (such as to sink it in the side pocket), ball A needs to be moving at a high speed V1A (meaning you would have to hit ball A quite hard with the cue). This is because only a very small fraction of the momentum of ball A (and therefore velocity) is transferred to ball B, due to the obliqueness of the impact.
For the case where the impact is head on (θ = 90°) the above solution does not apply. In this case V2A = 0 and V2B = V1A. This essentially means that the velocity of ball A is completely transferred to ball B.
For a more detailed and complete analysis, in which the trajectory of ball A is calculated (after impact), under the influence of friction between the ball and billiard table, see the problem, Cue ball trajectory with table friction.
The Sweet Spot
The physics of billiards is similar to the Physics Of Hitting A Baseball, in that there is also a sweet spot on a billiard ball where you can strike with the cue stick so that no friction force develops between the ball and the billiard table. Knowing the location of this sweet spot can give you an idea of where to hit the ball so that it develops backspin or forward spin, which can be useful when making a shot.
Consider the figure below showing the position of the cue at height h.
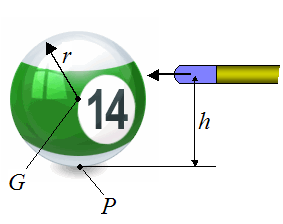
We wish to find the height h so that no (horizontal) frictional force develops at point P when the ball is struck by the cue.
Analysis Of The Sweet Spot
In this analysis, we can represent the ball + cue system with a free-body diagram as shown below.
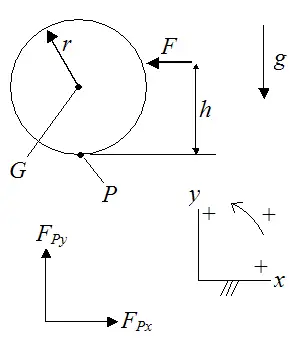
Where:
F is the force the cue exerts on the ball when it strikes
r is the radius of the ball
G is the center of mass of the ball
g is the acceleration due to gravity, which is 9.8 m/s2
P is the point of contact of the ball with the billiard table
FPx is the x-component of the force exerted on the ball by the billiard table, at point P. This is a frictional force.
FPy is the y-component of the force exerted on the ball by the billiard table, at point P.
By Newton's Second Law, the general force equation in the x-direction is:
Where:
m is the mass of the ball
aGx is the acceleration of the center of mass in the x-direction
This equation becomes
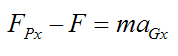
Since FPx = 0 we get
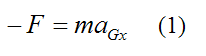
By Newton's Second Law, the general force equation in the y-direction is:
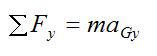
where aGy is the acceleration of the center of mass in the y-direction.
Since the billiard ball only moves in the x-direction aGy = 0, so the above equation becomes
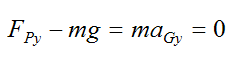
Therefore
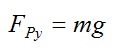
We must now write the general moment equation for rotation of a rigid body about its center of mass G.
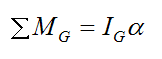
Where:
ΣMG is the sum of the moments about the center of mass G
IG is the moment of inertia of the ball about its center of mass, about an axis pointing out of the page
α is the angular acceleration of the ball
Since no frictional force develops between the ball and table, there is no relative slipping at point P. This means that we have a case of pure rolling. Thus, we can write the following:
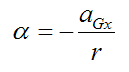
In the above equation the negative sign is there to match the sign convention used in this problem.
The moment equation becomes
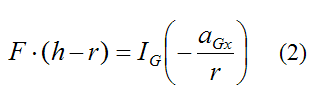
Combine equations (1) and (2) and we get
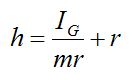
For a solid sphere
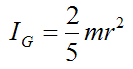
Therefore
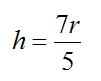
This is the height to hit the ball so that no friction develops at point P. No matter how hard you hit the ball at this location, no friction (reaction) force will develop at point P. Therefore, pure rolling of the ball will always result after impact (no relative slipping).
In the cases where the cue strikes above or below this height h, friction is necessary to prevent the ball from slipping on the surface of the billiard table. And if the ball is hit hard enough (above or below height h) relative slipping will occur, due to insufficient friction between ball and table.
In the cases where slipping occurs we have the following inequality:
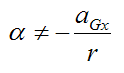
This means that there is relative motion between the ball and billiard table at point P immediately after impact. In other words (immediately after impact), the tangential velocity of the ball at point P is not equal in magnitude and opposite in direction to the velocity of the center of mass of the ball G.
In the case of pure rolling, the tangential velocity of the ball at point P is equal in magnitude and opposite in direction to the velocity of the center of mass of the ball G. Therefore, the velocities cancel out and there is no relative slipping at point P.
Relative Slipping Analysis
Relative slipping between ball and billiard table is an interesting point of analysis. It's informative to understand how the ball moves depending on where it is hit relative to h.
Consider the figure below.
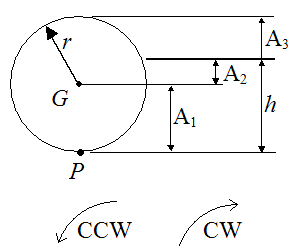
When the ball is hit sufficiently hard with a leftward force in region A1 the ball is given a leftward velocity, and is given a backspin in the CW direction. Relative slipping occurs at point P, and the resulting frictional force at this location is pointing right. The leftward velocity of the ball decreases and it accelerates to the right due to the direction of the frictional force. The rate of backspin decreases due to the direction of the frictional force. This occurs until relative slipping at point P stops and pure rolling occurs.
When the ball is hit sufficiently hard with a leftward force in region A2 the ball is given a leftward velocity, and is given a forward spin in the CCW direction. Relative slipping occurs at point P, and the resulting frictional force at this location is pointing right. The leftward velocity of the ball decreases and it accelerates to the right due to the direction of the frictional force. The rate of forward spin increases due to the direction of the frictional force. This occurs until relative slipping at point P stops and pure rolling occurs.
When the ball is hit sufficiently hard with a leftward force in region A3 the ball is given a leftward velocity, and is given a forward spin in the CCW direction. Relative slipping occurs at point P, and the resulting frictional force at this location is pointing left. The leftward velocity of the ball increases and it accelerates to the left due to the direction of the frictional force. The rate of forward spin decreases due to the direction of the frictional force. This occurs until relative slipping at point P stops and pure rolling occurs.
Thus, the nature of the slipping will change depending on which of the regions, (A1, A2, A3), the cue stick strikes the ball.
Note that for the three cases above, the frictional force that develops due to relative slipping is known as kinetic friction. Kinetic friction occurs when there is "rubbing" between two surfaces. This type of friction always opposes the direction of motion. So for example, if a crate is sliding on the floor in the left direction, the kinetic friction between the crate and floor acts to the right. In the cases where we have this type of friction you have to account for the direction of relative slipping and then assign the direction of friction to be in the opposite direction.
On the other hand, when there is no relative slipping between two surfaces the frictional force between them is known as static friction. So in the general cases where the billiard ball experiences no relative slipping at point P, we have static friction maintaining pure rolling. Accounting for static friction differs from kinetic friction in that you don't need to know the direction in which it acts. The direction is solved for in the dynamics equations. So in this sense it is easier to account for static friction than kinetic friction.
A Closer Look At Relative Slipping (optional)
This is a continuation of the previous section, with a more in-depth look at relative slipping. This section is optional, so you may skip it if you like.
The figure below shows a free-body diagram of a billiard ball experiencing a general case of relative slipping.
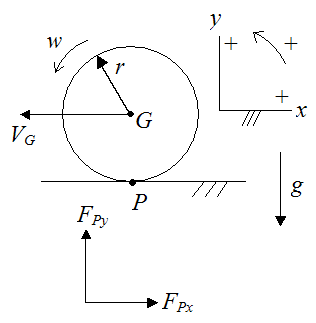
Where:
VG is the velocity of the center of mass of the ball. (In practical terms, when one refers to the velocity of the ball he is referring to the velocity of the center of mass of the ball).
w is the angular velocity of the ball
Let wi represent the initial angular velocity of the ball immediately after impact.
Let VGi represent the initial velocity of the ball immediately after impact.
With no loss of generality we can assume VGi is to the left (negative, according to the sign convention) and wi is either CW (negative) or CCW (positive).
If the cue strikes the ball in region A3 and relative slipping occurs, then
wir > -VGi.
If the cue strikes the ball anywhere below height h and relative slipping occurs, then wir < -VGi.
Set
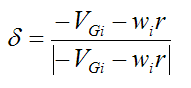
This is equal to +1 or -1. This factor accounts for the direction of relative slipping, which is important to know since we are dealing with kinetic friction. Such factors are mathematically very convenient when accounting for the direction of kinetic friction. (Note that |x| means the absolute value of x).
From before
This is the normal force acting on the ball at point P.
The general force equation in the x-direction is:
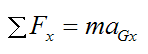
The kinetic friction acting at P is given by:
where μk is the coefficient of kinetic friction between the ball and table.
Now,
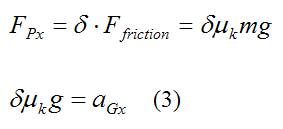
The general moment equation for rotation of a rigid body about its center of mass G is:
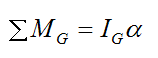
This becomes
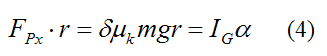
From equations (3) and (4) we get:
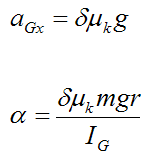
The linear velocity of the ball is:
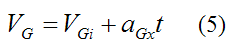
where t is time
The angular velocity of the ball is:
We wish to find the time it takes for the ball to stop slipping, and begin pure rolling. Thus, using equations (5) and (6) we can formulate the following equality, which holds true when there is pure rolling:
From this we can solve for time t.
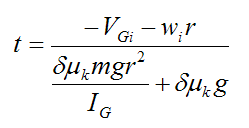
For a solid sphere
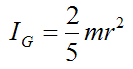
Therefore
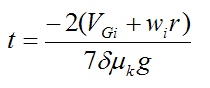
Let's now find the distance traveled by the ball before pure rolling begins, using the time t from above.
The distance d is:
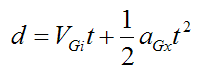
A final consideration is finding the velocity of the ball before pure rolling begins. To do this we calculate the velocity VG using the time t from above.
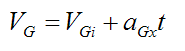
Note that the above three equations are only valid as long as there is relative slipping at point P.
Sample Calculation For Relative Slipping
This is a sample calculation using the results of the previous section.
VGi = -1 m/s (initial leftward velocity)
wi = -20 rad/s (backspin, CW rotation)
r = 0.028 m
μk = 0.3
g = 9.8 m/s2
δ = 1
aGx = 2.94 m/s2 - calculated from equation (3)
Therefore the time it takes the ball to stop slipping is
t = 0.15 s
The distance traveled by the ball during slipping is
d = -0.12 m (the ball has traveled to the left)
The velocity of the ball just before pure rolling begins is
VG = -0.56 m/s (leftward velocity)
Closing Remarks
As you can see, the physics of billiards can get pretty involved when you start considering all the things that can happen in a typical game of pool. You can bet that professional players are very proficient in the practical usage of the physics presented here, as well as other aspects of the game not discussed here.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.