About me and why I created this physics website.

Moment Of A Force

This page is a continuation of the discussion on torque.

The moment of a force (also known as torque) provides a measure of the tendency of that force to cause rotation about a given point (or axis).

It is calculated based on the following XYZ reference frame with sign convention shown.



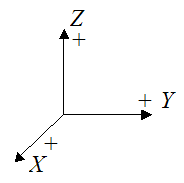
The positive direction of the three individual axes is defined as shown. This choice of positive direction for these axes is important because the moment of a force is calculated using vector cross-product multiplication, the mathematics of which is based on this choice of sign convention for XYZ. So it is important to use this same sign convention. If you use another sign convention when solving dynamics problems, you might get the wrong answer.

Define the following:

r is the position vector from an arbitrary point O to the point where the force vector F is acting on a body. The vector components of r and F are:



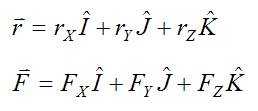
where I, J, K are unit vectors pointing along the positive X, Y, Z axes (respectively).


The moment of the force F about O is defined as:



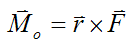
Carrying out the vector cross-product multiplication we get




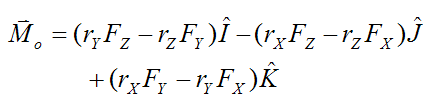
Now, there are certain problems in which we wish to solve for the moment M_o, but not the forces causing M_o. An example of such a problem is one in which there is an equal and opposite force pair acting on the body, as shown in the figure below.



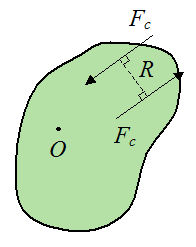
where F_c are two parallel forces acting in opposite directions anywhere on the body, and R is the perpendicular distance between these forces. This pair of forces is commonly called a force couple. They exert a pure moment.

It is interesting that no matter where point O is located relative to this force pair, the resultant moment due to them will always have the same direction and the same magnitude relative to point O. The direction of the resultant moment is given by the right hand rule and it is perpendicular to the plane containing the force pair. The magnitude of the resultant moment is given by



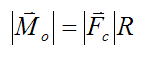
There are specific problems where force couples occur; such as joint locations, where the distance R is small and the force F_c is large.


The moment due to a force couple pair can be simply expressed as:



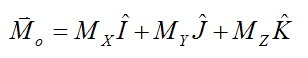
For certain problems involving force couples, we can solve for the unknowns M_X, M_Y, M_Z in the dynamics equations, without needing to solve for either R or F_c. For example, in the analysis of gyroscope physics this is done.

Note that moments due to force couples only show up in the moment (e.g. Euler) equations. But they do not show up in the force equations (Newton’s Second law, F = ma), since a force couple pair cancels out.

As a result, moments due to force couples contribute only to rotation of a body but not to the translation of a body (due to Newton’s Second Law) – more specifically, this means they do not contribute to the acceleration of the center of mass of a body.



Return to Dynamics page


Return to Real World Physics Problems home page