About me and why I created this physics website.

Equations Of Motion

Equations of motion mathematically describe the motion of a system under the influence of forces. In particular, these equations describe the motion of particles or bodies subjected to different forces.

Equations of motion relate the forces acting on a system to the motion of the system. These equations are generally the most useful because they allow for the direct solution of a dynamics problem, as a function of time. Using these equations one can determine the "behaviour" of a system over time, which can give important information as a result. On the other hand, solving dynamics problems using energy or momentum methods is generally only done if one wishes to determine the final state of a system based on some initial state, without regard for what happens "in between".

As mentioned, the equations of motion can apply either to particles or bodies of finite size. The choice to treat an object as a particle is generally done when: (1) Rotational effects are unimportant (or negligible), or (2) When the size of the object is negligible relative to the scale of the system, so that only translational motion is relevant. An example of (1) is when analyzing the translational motion of billiard balls, as they collide with each other. An example of (2) is when analyzing the translational motion of planets in the solar system, which are very small compared to the size of the solar system.

Rotational motion is therefore irrelevant when treating an object as a particle. Therefore, the equations of motion for a particle are equations for translational motion. These equations are given here as scalar equations:



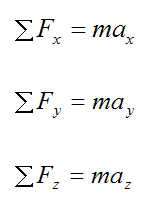
Where:

m is the mass of the particle

ΣF_x is the sum of the forces in the x-direction

ΣF_y is the sum of the forces in the y-direction

ΣF_z is the sum of the forces in the z-direction

a_x is the acceleration of the particle in the x-direction, with respect to an inertial reference frame

a_y is the acceleration of the particle in the y-direction, with respect to an inertial reference frame

a_z is the acceleration of the particle in the z-direction, with respect to an inertial reference frame

Here, the x, y, z directions are based on a three-dimensional (Cartesian) coordinate system with arbitrary orientation.


The equations of motion for a rigid body are given on the page on Rigid Body Dynamics.

The equations of motion for a rigid body include additional equations which account for rotation (in addition to translation). The most general type of motion an object experiences is translational plus rotational motion. Therefore, the complete equations of motion must account for both of these types of motion.


Lagrangian Mechanics

Using the Lagrangian method one can find the equations of motion for a system in a straightforward fashion, without having to go through a Newtonian analysis, in which you have to consider the forces acting on the system and assign directions, etc. This can save some time and effort. However, the catch is that the Lagrangian method only works when there are conservative forces acting on the system, and there is no friction anywhere. Furthermore, you can lose some "feel" for the problem since you are going directly to the mathematics rather than analyzing the physics first (which comes from considering the forces acting on the system). So it is perhaps not a good idea to use this method if you are still gaining proficiency solving classical mechanics problems. However, if you are already an experienced problem solver, the Lagrangian method is an efficient way to solve problems, saving you time and effort.



Sign Convention

When solving problems using the equations of motion, it is important to set up a sign convention and use that sign convention consistently.

Now, there are instances where the choice of sign convention matters and other instances where it does not. However, there are cases where certain mathematical operations are based on a certain sign convention (such as the vector cross-product), so it is important to use this same sign convention either when using those same mathematical operations or when using equations that are derived based on those mathematical operations. For example, the vector cross-product is used to derive the Euler equations of motion, so when solving problems using these equations, the same sign convention must be used. As a result, the right-hand rule applies. This leads me to the following important points concerning the solution of problems using the equations of motion.

If you know the direction of spin of the angular velocity, you must use the right-hand rule to assign the correct direction for its corresponding vector, and thus determine the correct values for its three components (w_x, w_y, w_z). Similarly, if you know the direction of spin of the angular acceleration, you must use the right-hand rule to assign the correct direction for its corresponding vector, and thus determine the correct values for its three components (α_x, α_y, α_z).

Conversely, if you know the components of the angular velocity vector (w_x, w_y, w_z), or the angular acceleration vector (α_x, α_y, α_z), the direction of spin is given by the right-hand rule.

The right-hand rule is consistent with the cross-product multiplications carried out in the derivation of the Euler equations of motion, and is therefore consistent with the choice of sign convention shown here, for xyz. This again stresses the importance of using the sign convention given here when solving problems using these equations. This sign convention is standard in physics books.

The right-hand rule also applies to the sum-of-moments vector (e.g. ΣM_G). To determine the correct direction for this vector, you can use the right-hand rule. However, if you are calculating this vector directly using cross-product multiplication (e.g. ΣM_G=Σr×F, where r is the position vector and F is an external force vector), then you do not need to apply the right-hand rule to determine its direction. This is because the resultant vector (calculated from Σr×F), is automatically pointing in the correct direction.

See the page on moment of a force for further explanation.


The sign convention that must be used for the equations of motion is shown below:




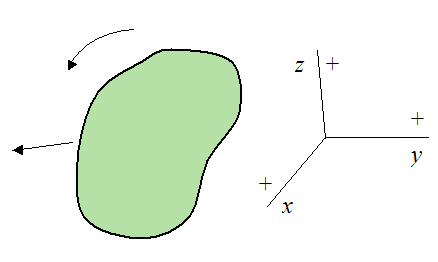
Furthermore, any different orientation of this sign convention in three-dimensional space can also be used. Examples of different orientations are shown below.

Example 1




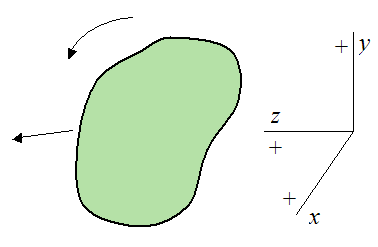
Example 2




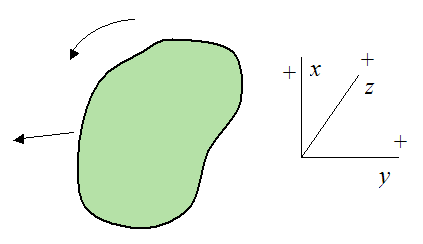
Example 3




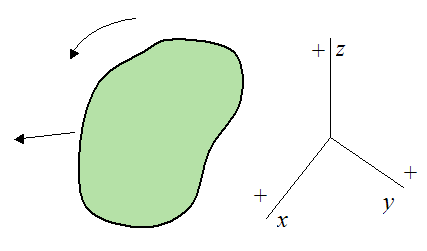
Now, an example of a sign convention that is not used in the derivation of the equations of motion is shown below.



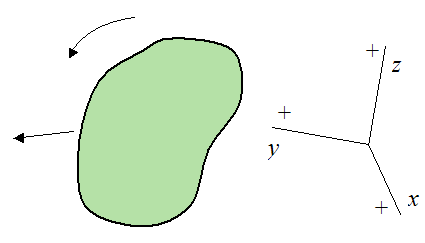
Use of this above sign convention may lead to errors when solving problems using the equations of motion.


As mentioned, there are cases where the choice of sign convention doesn’t matter, but rather than attempt to list all these cases it is better to just be on the safe side and use the sign convention given here for solving problems using the equations of motion. You will never go wrong.


By extension, when applying momentum and/or energy equations to solve a problem, use the sign convention given here, and you will never go wrong.


The final important point to make on sign convention is the use of Newton's Second Law equation, where



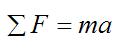
When using this equation, don’t assume a direction for the acceleration (a) if it is unknown. Instead leave it as-is. For instance, don’t assume that acceleration is in the negative direction, resulting in the following:



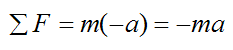
Now, there are cases where it doesn’t matter and you will get the same answer, such as when solving some problems using algebraic equations. But there are other cases where it does matter, such as when solving problems using differential equations. For example, let’s say we have a spring-mass system as shown below.

Let x be the displacement of the spring from its equilibrium (unstretched) length. The sign convention is: positive is to the right, negative is to the left.




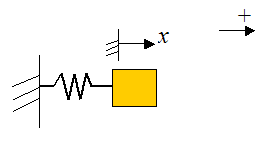
Draw a free-body diagram for the block.



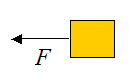
The force F acting on the block is due to the restoring force of the spring. This force is given by



where k is the spring constant, assuming Hooke's Law.

By Newton’s Second Law,



where m is the mass of the block, and a is the acceleration of the block.

Equating the above two equations we get



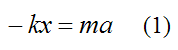
Without loss of generality, we can say that the displacement x of the spring is equal to the position of the block. Therefore, the acceleration of the block is equal to the second derivative of x, with respect to time. Thus,



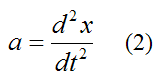
Substitute this into equation (1) and we have



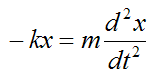
This becomes the differential equation:



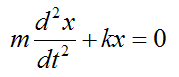
which has the general solution




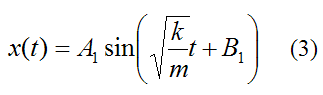
Now, if we were to assume that the acceleration of the block is in the negative x-direction, then from equation (1) we have



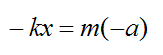
Substituting equation (2) we get



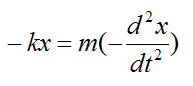
This becomes the differential equation:



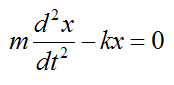
which has the general solution



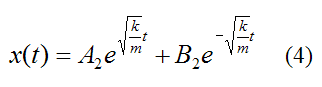
This solution is different from equation (3). So clearly, it was not a good idea to assume a negative direction for the acceleration, since we got a different answer. It turns out that equation (3) is the correct solution and equation (4) is wrong.

As it turns out, the right side of equation (2) correctly accounts for the direction of acceleration of the block, given some x = x(t). For example, if x = 2t², then d²x/dt² = 4, and the acceleration is pointing to the right (according to the sign convention used). If instead we use -d²x/dt² this gives an acceleration of -4, which is pointing to the left. This is clearly wrong!


So to be on the safe side, if the acceleration is unknown just leave it as-is in the equation F = ma (i.e. don’t assume a direction for it), and you will never go wrong. Ultimately, the acceleration will always point in the direction of the resultant forces, anyway.

The same idea applies for unknown angular velocity terms and unknown angular acceleration terms in the equations of motion (such as in the Euler equations). If any of them are unknown then don’t assume a direction for them. Let their direction (and magnitude) be solved for in the solution.

Thus, when assigning direction for the various unknown quantities in the equations of motion (Newton's Second Law equations, and the Euler equations) only do so for the forces and moments.


By extension, when applying momentum and/or energy equations to solve a problem, if the linear velocities and/or the angular velocities are unknown, just leave them as-is. Don't assume a direction for them, and you will never go wrong.


Now, there may be instances where (based on the kinematics of the problem) you have to relate the angular acceleration and/or angular velocity to the linear acceleration and/or linear velocity, of the various bodies. This is done by introducing additional equation(s), where for example, negative angular acceleration means positive linear acceleration, or positive angular acceleration means negative linear acceleration. For example, let’s say we have a ball rolling without slipping on a surface, as shown below, along with the sign convention used (the positive z-axis is pointing out of the page).



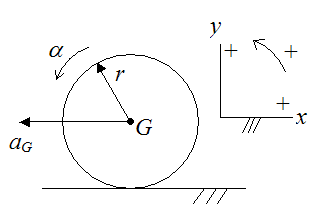
From the kinematics of the problem,



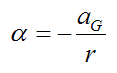
This equation is combined with the equations of motion for solving the problem.


In summary, there are three points to always follow when dealing with signs and sign convention:

(1) Use the sign convention given here.

(2) When assigning direction for the various unknown quantities in the equations of motion (Newton's Second Law equations, and the Euler equations) only do so for the forces and moments. For the unknown acceleration/velocity terms in the equations, don’t assume a direction for them. Just leave them as-is. The solution will tell you what direction they are in.

(3) For instances where (based on the kinematics of the problem) you have to relate the angular acceleration and/or angular velocity to the linear acceleration and/or linear velocity, you can do so by introducing additional equations, as shown in the example above.


Final Note On Sign Convention: When you solve the equations of motion for a particular problem and you get positive values for the forces and/or moments, this means that they are acting in the direction you assumed, in your free-body diagram. On the other hand, if you get negative values for the forces and/or moments, this means that they are acting in the opposite direction that you assumed in your free-body diagram.



Return to Dynamics page


Return to Real World Physics Problems home page