About me and why I created this physics website.
Conservative Force
A conservative force is a force that acts on a particle, such that the work done by this force in moving this particle from one point to another is independent of the path taken. To put it another way, the work done depends only on the initial and final position of the particle (relative to some coordinate system). Two examples of conservative forces are gravitational forces and elastic spring forces.Gravitational Force
Suppose there is a gravitational force acting on a particle, as shown below.
The gravitational force acting on the particle is pointing in the direction of gravity and its magnitude is equal to mg, where m is the mass of the particle, and g is the acceleration due to gravity. The particle moves from A to B and its change in vertical height is Δh (along the direction of gravity). The arbitrary path traveled by the particle is represented by the blue curve. The arbitrary path traveled by the particle may be due to the presence of other forces also acting on the particle, but we do not need to analyze them, since the gravitational force is unaffected by them and can therefore be treated independently.
The work done by gravity in moving the particle is dependent only on the change in vertical height (displacement) Δh of the particle, as it moves from A to B. Therefore, the work done is only dependent on the position of A and B.
If Δh is equal to the final vertical position (at point B) minus the initial vertical position (at point A) then the work (Wg) done by gravity on the particle is given by the following scalar equation:
A negative sign is present in the above equation because vertical displacement (Δh) acting in the same direction as gravity (Δh < 0) must yield positive work, and vertical displacement acting in the opposite direction of gravity (Δh > 0) must yield negative work. So, if B is lower than A we have Δh < 0, and the negative sign accounts for this, making the work positive. On the other hand, if B is higher than A we have Δh > 0, and the negative sign accounts for this, making the work negative.
The expression for Wg is useful because no matter how complicated the path from A to B is, we only need to know the change in vertical position of the particle, and we can find the work done on the particle by gravity. Therefore, gravity is a conservative force.
Now, if we have a body instead of a particle, the same analysis applies. We simply treat the center of mass of the body as a particle, and apply the above procedure to find the work done by gravity. In other words, if we want to find the work done by gravity on the body we look at the motion of its center of mass, and then apply the equation above for Wg. This is shown below. The red dot represents the center of mass of the body. The mass of the body is given by m.
The work done by gravity on the body is dependent only on the change in vertical height Δh of the center of mass of the body, as it moves from A to B.
If Δh is equal to the final vertical position (at point B) of the center of mass minus the initial vertical position (at point A) of the center of mass, then the work (Wg) done by gravity on the body is given by the following scalar equation:
Note that it doesn’t matter at all how the body moves. We only need to know the change in vertical position of its center of mass (as it moves from A to B) to determine the work done on the body by gravity. Therefore, gravity is a conservative force.
Elastic Spring Force
Consider a spring force acting on a particle, as shown below. The spring is attached to a wall at point O, where it can pivot. At position A of the particle, the spring is stretched or compressed by an amount s1 from its equilibrium (unstretched) position. At position B of the particle, the spring is stretched or compressed by an amount s2 from its equilibrium position. The arbitrary path traveled by the particle from A to B is represented by the blue curve.
Note that the dashed line represents the equilibrium position of the spring, where the spring is unstretched. Once again, the possible presence of other forces acting on the particle is irrelevant to this discussion, since we are only focusing on the work done by the spring.
The work done by the spring (Ws) on the particle as it moves from A to B is given by the following scalar equation:
where k is the spring constant.
For the above equation we are assuming we have a spring that obeys Hooke's Law.
Therefore, the work done by the spring on the particle depends only on the position of A and B (relative to the position of point O), since this is what determines the amount of stretch or compression in the spring (s1 and s2). Therefore, an elastic spring is a conservative force.
If we replace the particle with a point on a body (to which the end of the spring is attached), the work done by the spring on the body is also given by the above equation. The figure below illustrates this situation.
The work done by the spring on the body is dependent only on the amount the spring is stretched or compressed from its equilibrium position, as it moves from A to B.
The work done by the spring (Ws) on the body is given by the following scalar equation:
Note that it doesn’t matter at all how the body moves. We only need to know the amount the spring is stretched or compressed from its equilibrium position (as it moves from A to B) to determine the work done by the spring on the body. Therefore, an elastic spring is a conservative force.
Knowing if a force is conservative is very useful for solving problems using energy calculations, since you only have to know the initial and final position where the force is acting. You don’t need to know the path traveled in between.
Conservative forces do zero work in those cases where the points (or particles) upon which the forces act, return to their original position. As a result, if a system is acted on by only conservative forces (such as gravity, or a spring), and that system returns to its original position, then that system will experience no net loss or gain of energy, due to those forces. Energy will thus be conserved for the system.
Non Conservative Forces
A non conservative force is a force that acts on a particle (or point), such that the work done by this force in moving this particle from one point to another is dependent on the path taken. To put it another way, the work done depends on the path itself. For example, a friction force is non conservative because the work done by friction always acts in the direction of travel and therefore depends on the length L of the path taken, as shown below.
The same reasoning applies if friction is acting on a body. The work done by the friction force depends on the path traveled by that area on the body acted upon by the friction force.
Thus, if a system is acted on by a non conservative force (such as friction), and that system returns to its original position, then that system will experience a net loss of energy, due to those forces. Energy will thus not be conserved for the system. This makes sense intuitively since we know friction is a source of energy loss. This is why we always try to minimize friction in moving parts and machine components so as to minimize the energy wasted.
A Closer Look At Conservative Forces (optional section)
Using Calculus, we can set up a general expression for the work done by a force vector F acting on a particle (or point) as the particle moves from position A to position B (see figure below).
Let |dr| represent an infinitesimal distance traveled by the particle at any point P, on the path traveled (represented by the blue curve). This distance |dr| is in the direction tangent to the path traveled, at point P.
Let dW represent the infinitesimal work done by the force vector F acting on the particle, over the distance |dr|, at point P. Therefore,
where θ is the angle the force vector F makes with the tangent to the curve at point P (as shown).
Using the vector dot product, the previous equation can be rewritten as:
where dr is the infinitesimally short vector, that is tangent to the blue curve at point P. Note that the above equation is a scalar equation.
Now, let
Where:
Fx, Fy, Fz are the components of the force F (along x,y,z).
dx, dy, dz are the infinitesimal components of the infinitesimally short vector dr (along x,y,z), that is tangent to the blue curve at point P.
Substituting into the above equation for dW we have
The total work (W) done by the force F on the particle as it moves from position A to B is:
If F is conservative this means that it depends only on the initial and final position of the particle at points A and B. We can therefore say that, if F is conservative, the above integral is equal to the difference in some function between A and B, given by:
where φ(x,y,z) is some function satisfying the above equation.
In other words, the work W can be expressed as a function that depends only on x,y,z.
The above equation for work is analogous to the work done by a conservative gravitational force, and a conservative spring force, that is dependent only on the positions A and B (discussed earlier).
Without loss of generality, we can say that the position of the particle on the blue curve is represented by three functions for x,y,z in terms of time t:
Now,
Substituting these into equation (1) we get
Now if,
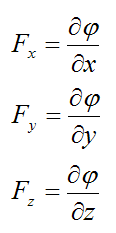
The above integral can be rewritten as
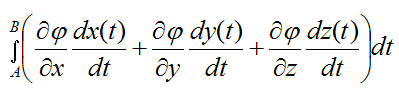
By the chain rule for partial derivatives, the term in brackets is equal to dφ/dt.
Therefore,
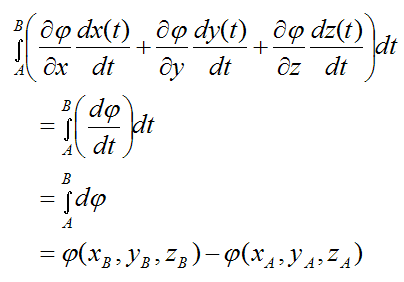
This result is very important. It says that a force field F(x,y,z) is conservative if and only if there exists a function φ(x,y,z), such that:
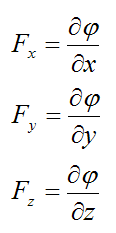
For example, the force field due to gravity acting on a body of mass m is equal to
where we define gravity as pointing in the negative z-direction.
Therefore, by comparison
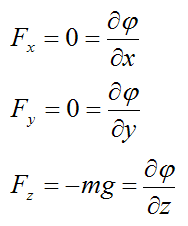
These above three equations are satisfied by
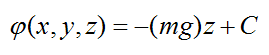
where C is a constant. Therefore a function φ(x,y,z) exists and the force field due to gravity is proven to be a conservative force, as expected.
If a function φ(x,y,z) does not exist then the force field F(x,y,z) is non conservative.
Return to Dynamics page
Return to Real World Physics Problems home page
