About me and why I created this physics website.

Rolling Resistance

Rolling resistance is the resistance to rolling that occurs when a round object, such as a ball, wheel, or cylinder rolls on a surface. It is caused primarily by deformation of the object, deformation of the surface, or both.

Rolling resistance is often neglected when solving problems involving rolling. For example, when modeling a cylinder rolling on a flat surface, it is often assumed that the cylinder and surface are rigid. This means that the cylinder and surface are made up of very hard material. Under this assumption there is no deformation of the cylinder at the contact location, and no deformation of the surface underneath the cylinder. As a result, the cylinder will continue rolling indefinitely (further assuming that there is no frictional resistance with the air). This means there is no rolling resistance, which can slow down the cylinder.

It is informative to analyze the dynamics of a uniform cylinder rolling on a flat horizontal surface, using the rigidity assumption.

Consider the figure below illustrating the motion of a uniform cylinder on a flat horizontal surface, and with sign convention shown. The cylinder rolls without slipping. This is modeled as a two-dimensional problem.



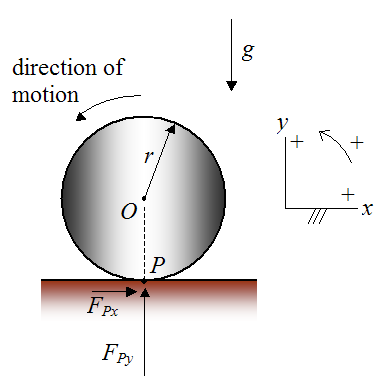
Where:

r is the radius of the cylinder

O is the geometric center of the cylinder. For a uniform cylinder this point coincides with the center of mass

F_Px is the resultant horizontal reaction force acting on the cylinder at point P, which is the contact point between the cylinder and surface

F_Py is the resultant vertical reaction force acting on the cylinder at point P

g is the acceleration due to gravity


Apply Newton’s Second Law in the x-direction:



Where:

m is the mass of the cylinder

a_Gx is the acceleration of the center of mass G of the cylinder in the x-direction, with respect to ground. For a uniform cylinder, the center of mass coincides with the geometric center O


Apply Newton’s Second Law in the y-direction:



where a_Gy is the acceleration of the center of mass G of the cylinder in the y-direction, with respect to ground. This acceleration is zero because the cylinder is rolling on a flat horizontal surface.

Therefore,



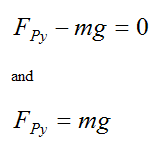
Next, apply the moment equation for rotation of a rigid body about its center of mass G (which coincides with the geometric center O):



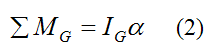
Where:

ΣM_G is the sum of the moments about point G

I_G is the moment of inertia of the cylinder about point G, about an axis pointing out of the page

α is the angular acceleration of the cylinder, with respect to ground


Now,



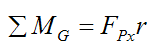
Substituting this into equation (2) we have




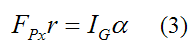
Since the cylinder is rolling with no slipping we can write:



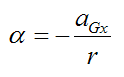
This is in accordance with the sign convention used.

Combining this equation with equation (1) we have



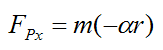
Combining this equation with equation (3) we have



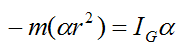
Since the angular acceleration α is common to both sides of this equation and I_G cannot be a negative number, the only possible solution is α = 0. This means that the cylinder will continue rolling indefinitely without slowing down, under the rigidity assumption.

However, we know from real life that the cylinder will slow down and eventually stop. In other words, we know that rolling resistance exists.

So we conclude that there must be some deformation at the contact interface, which causes the cylinder to slow down and eventually stop. With this new understanding we can now come up with a new solution, which captures the physics of this.

Consider the new figure below illustrating the motion of a uniform cylinder on a flat horizontal surface. For simplicity, let’s assume that the cylinder itself is rigid and the surface underneath is deforming due to the weight and motion of the cylinder. As before, assume that the cylinder rolls without slipping.

As before, this is modeled as a two-dimensional problem. The set up of this problem will be a bit different from before.

A new variable d is introduced, which represents the horizontal distance from the vertical line passing through point O to the point of action P of the resultant forces F_Px and F_Py. The distance d is assumed to be small.




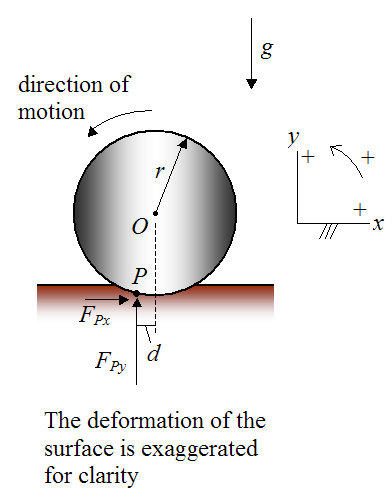
Apply Newton’s Second Law in the x-direction:




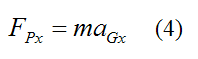
Apply Newton’s Second Law in the y-direction:



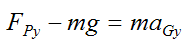
Since a_Gy = 0 we get




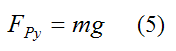
Next, apply the moment equation for rotation of a rigid body about its center of mass G (which coincides with the geometric center O):



Now, since d is assumed to be small,



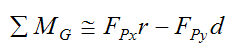
Substituting this into equation (6) we have



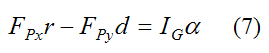
Since the cylinder is rolling with no slipping we can write:



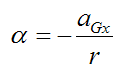
This is in accordance with the sign convention used.


Combining this equation with equation (4) we have



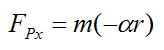
Combining this equation with equation (7) we have



Substitute equation (5) and we get



For a uniform cylinder,



Therefore equation (8) becomes



Solving for angular acceleration we get



This tells us that the angular acceleration of the cylinder is negative, which makes sense since we know that the cylinder experiences rolling resistance, and slows down as a result.

Note that the resultant forces F_Px and F_Py must act to the left of the vertical line passing through point O. If the resultant forces were to act to the right of the vertical line passing through point O, the distance d would be taken as negative and the angular acceleration α would be positive. This would mean that the cylinder would speed up, which we know is impossible.


Rolling At Constant Speed

The fact that the cylinder tends to slow down means that it takes a constant force to overcome rolling resistance and keep the cylinder rolling at a constant speed. We can find an expression for this force. Let’s call this force F and solve for it using the same basic procedure as before. The set up is illustrated in the figure below.

Let’s assume that the applied force F is acting horizontally at the geometric center O of the cylinder.




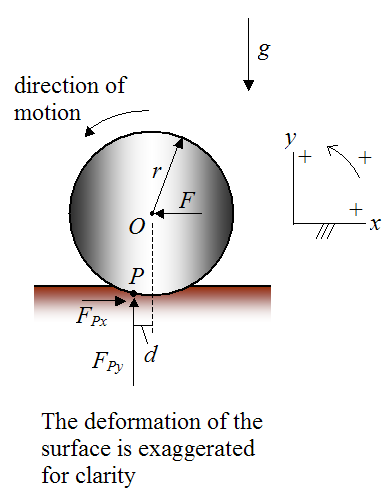
Since the cylinder is rolling at constant velocity with no slipping, its angular acceleration is zero and its center of mass (coinciding with point O) has zero acceleration.

Apply Newton’s Second Law in the x-direction:




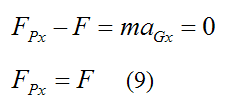
Apply Newton’s Second Law in the y-direction:



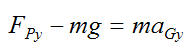
Since a_Gy = 0 we get




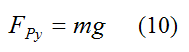
Next, apply the moment equation for rotation of a rigid body about its center of mass G (which coincides with the geometric center O). However, since the cylinder is rotating at constant speed (in equilibrium) we can sum the moments about any point.



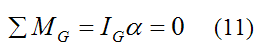
Now, since d is assumed to be small,



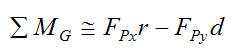
Substituting this into equation (11) we have



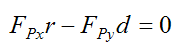
Substituting equations (9) and (10) into the above equation we get



Therefore the force F is




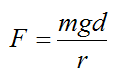
So, to minimize the rolling resistance (and minimize F) we want to keep the distance d as small as possible. One way to do this is to make the cylinder and rolling surface as rigid as possible. This explains why tires on vehicles should be kept well inflated, since tires that are under inflated will be less rigid and will deform more on the road surface. Under inflated tires result in a greater distance d, thus increasing the rolling resistance (F), and decreasing the fuel economy.


As mentioned, rolling resistance is neglected in many problems that involve rolling. This means that, by assumption, there is negligible deformation at the contact interface, and we set d = 0 in the model. This is a reasonable assumption in those cases where there are other forces present, which (in comparison) far exceed the forces due to deformation at the contact interface. For example, let’s say we have a cylinder rolling down a steep incline (as a result of gravity pulling down on it). If we assume that d ≠ 0, the solution for the acceleration of the cylinder down the incline will be negligibly different from the solution where we assume that d = 0. In other words, deformation at the contact interface is not the dominant influence on the motion of a cylinder rolling down a steep incline (gravity is). Thus, it is only when we have a cylinder rolling on a flat horizontal surface, where forces due to deformation at the contact interface are the dominant influence, and must therefore be accounted for.



Return to Dynamics page


Return to Real World Physics Problems home page