About me and why I created this physics website.

Rotational Motion

Rotation About A Fixed Axis

Rotation about a fixed axis is a special case of rotational motion. It is very common to analyze problems that involve this type of rotation – for example, a wheel.

The figure below illustrates rotational motion of a rigid body about a fixed axis at point O. This type of motion occurs in a plane perpendicular to the axis of rotation.




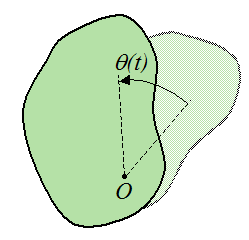
In the figure, the angle θ(t) is defined as the angular position of the body, as a function of time t. This angle can be measured in any unit one desires, such as radians, or degrees.

Every point in the rigid body rotates by the same angle θ(t).

Given the angular position of the rigid body we can calculate the angular displacement, angular velocity, and angular acceleration. These are important quantities to consider when evaluating the rotational kinematics of a problem.

A common assumption, which applies to numerous problems involving rotation about a fixed axis, is that angular acceleration is constant. With angular acceleration as constant we can derive equations for the angular position, angular displacement, and angular velocity of a rigid body experiencing rotation about a fixed axis.

The easiest way to derive these equations is by using Calculus. The derivations that follow are of the exact same form as the equations derived for rectilinear motion, with constant acceleration.

The angular acceleration is given by



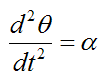
where α is the angular acceleration, which we define as constant.

Integrate the above equation with respect to time, to obtain angular velocity. This gives us



where w(t) is the angular velocity and C₁ is a constant.

Integrate the above equation with respect to time, to obtain angular position. This gives us



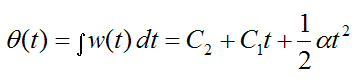
where θ(t) is the angular position and C₂ is a constant.


The constants C₁ and C₂ are determined by the initial conditions at time t = 0. The initial conditions are:

At time t = 0 the angular position is θ₁.

At time t = 0 the angular velocity is w₁.

Substituting these two initial conditions into the above two equations we get



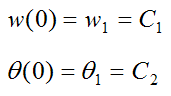
Therefore C₁ = w₁ and C₂ = θ₁.


This gives us




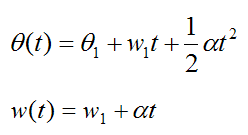
For convenience, set θ(t) = θ₂ and w(t) = w₂. As a result




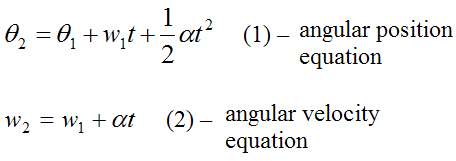
Angular displacement is defined as Δθ = θ₂−θ₁. Therefore, equation (1) becomes




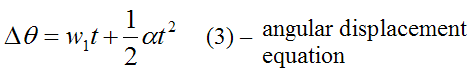
If we wish to find an equation that doesn’t involve time t we can combine equations (2) and (3) to eliminate time as a variable. This gives us




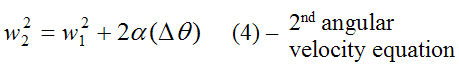
Equations (1), (2), (3), and (4) fully describe the rotational motion of rigid bodies (or particles) rotating about a fixed axis, where angular acceleration α is constant.

For the cases where angular acceleration is not constant, new expressions have to be derived for the angular position, angular displacement, and angular velocity. If the angular acceleration is known as a function of time, we can use Calculus to find the angular position, angular displacement, and angular velocity, in the same manner as before.

Alternatively, if we are given the angular position θ(t) as a function of time, we determine the angular velocity by differentiating θ(t) once, and we determine the angular acceleration by differentiating θ(t) twice.

For example, let's say the angular position θ(t) of a particle is given by



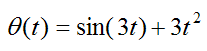
Thus, the angular velocity w(t) is given by



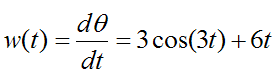
The angular acceleration α(t) is given by




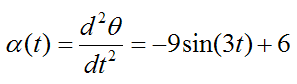
Velocity And Acceleration Of A Particle Traveling Around A Circle

The figure below shows a particle P traveling around a circle of radius R, with fixed center at O.



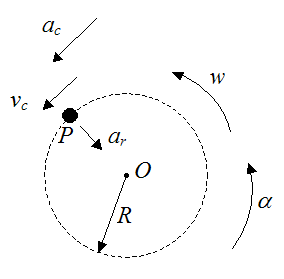
Where:

w is the angular velocity associated with the rotational motion of the particle P. This quantity is measured in rad/s

α is the angular acceleration associated with the rotational motion of the particle P. This quantity is measured in rad/s²

a_r is the radial acceleration of the particle P, pointing towards the center of the circle (this is commonly called centripetal acceleration)

v_c is the circumferential velocity of the particle P (this is tangent to the circle)

a_c is the circumferential acceleration of the particle P (this is tangent to the circle)


We can use the equations for curvilinear motion to derive expressions for a_r , v_c , and a_c. Since R is constant we get




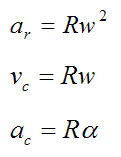
Note that there is no radial component of velocity pointing towards, or away from the center of the circle. This is because the radius R is constant. If R were to change with time there would be a radial component of velocity pointing towards, or away from the center of the circle – From the page on curvilinear motion this radial component would be equal to dR/dt, which is the rate of change of the radius with time.


If you want to test your understanding and solve some problems go to Circular Motion Problems.


Rotational Motion In Three Dimensions

Rotational motion in three dimensions is mathematically more complicated than planar rotation about a fixed axis, since the axis of rotation can change direction. This type of rotation applies to bodies experiencing three-dimensional motion. However, it is generally only necessary (and practical) to account for such rotation when determining the velocity and acceleration of a point on a body that is experiencing three-dimensional motion. As a result, three-dimensional rotation does not lend itself to a stand-alone discussion here.

For an explanation of three-dimensional motion see A closer look at velocity and acceleration.

For an example of a solved problem involving three-dimensional rotation see Gyro Top.



Return to Kinematics page


Return to Real World Physics Problems home page