About me and why I created this physics website.

Curvilinear Motion

General Curvilinear Motion

Curvilinear motion is defined as motion that occurs when a particle travels along a curved path. The curved path can be in two dimensions (in a plane), or in three dimensions. This type of motion is more complex than rectilinear (straight-line) motion.

Three-dimensional curvilinear motion describes the most general case of motion for a particle.

To find the velocity and acceleration of a particle experiencing curvilinear motion one only needs to know the position of the particle as a function of time.

Let’s say we are given the position of a particle P in three-dimensional Cartesian (x,y,z) coordinates, with respect to time, where




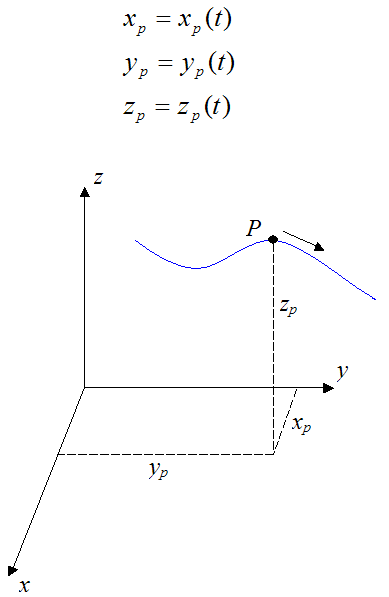
The velocity of the particle P is given by




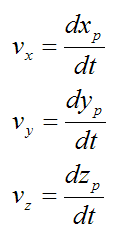
The acceleration of the particle P is given by




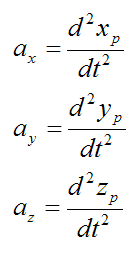
As you can see, if we know the position of a particle as a function of time, it is a fairly simple exercise to find the velocity and acceleration. You simply take the first derivative to find the velocity and the second derivative to find the acceleration.


The magnitude of the velocity of particle P is given by




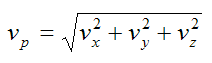
The magnitude of the acceleration of particle P is given by




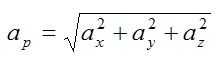
Note that the direction of velocity of the particle P is always tangent to the curve (i.e. the path traveled, denoted by the blue curve in the figure above). But the direction of acceleration is generally not tangent to the curve.

However, the acceleration component tangent to the curve is equal to the time derivative of the magnitude of velocity of the particle P (along the curve). In other words, if v_t is the magnitude of the particle velocity (tangent to the curve), the acceleration component of the particle tangent to the curve (a_t) is simply



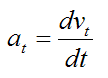
In addition, the acceleration component normal to the curve (a_n) is given by



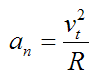
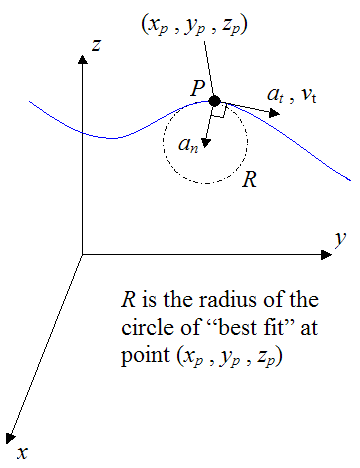
where R is the radius of curvature of the curve at a given point on the curve (x_p,y_p,z_p).

The figure below illustrates the acceleration components a_t and a_n at a given point on the curve (x_p,y_p,z_p).




For the specific case where the path of the blue curve is given by y = f(x) (two-dimensional motion), the radius of curvature R is given by



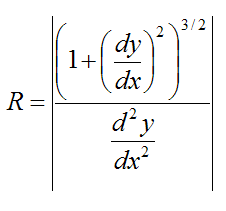
where |x| means the “absolute value” of x. For example, |-2.5| = 2.5, and |3.1| = 3.1.

However, it is usually not necessary to know the radius of curvature R along a curve. But nonetheless, it is informative to understand it on the basis of its relationship to the normal acceleration (a_n).


Curvilinear Motion In Polar Coordinates

It is sometimes convenient to express the planar (two-dimensional) motion of a particle in terms of polar coordinates (R,θ), so that we can explicitly determine the velocity and acceleration of the particle in the radial (R-direction) and circumferential (θ-direction). For this type of motion, a particle is only allowed to move along the radial R-direction for a given angle θ.

For a particle P defined in polar coordinates (as shown below), we can derive a general equation for its radial velocity (v_r), radial acceleration (a_r), circumferential velocity (v_c), and circumferential acceleration (a_c).

Note that the circumferential direction is perpendicular to the radial direction.




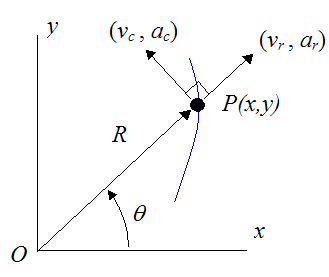
The position of the particle P is given with respect to time, where




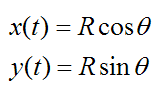
To find the velocity, take the first derivative of x(t) and y(t) with respect to time:




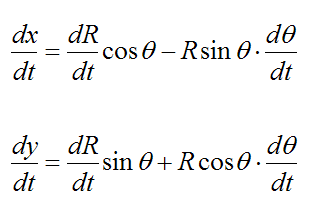
To find the acceleration, take the second derivative of x(t) and y(t) with respect to time:




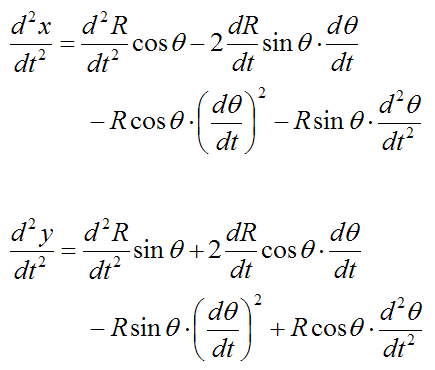
Without loss of generality we can evaluate the velocities and accelerations at angle θ = 0, knowing that (at this angle) radial velocity and radial acceleration is in the x-direction, and circumferential velocity and circumferential acceleration is in the y-direction.

Setting θ = 0 we have:






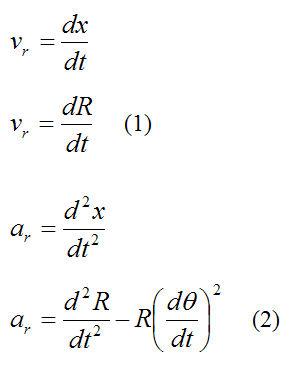
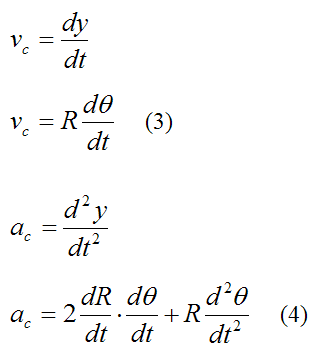
Equations (1), (2), (3), and (4) fully describe the curvilinear motion of a particle P in polar coordinates.

The term dθ/dt is called angular velocity. It has units of rad/s. One rad (radian) = 57.296 degrees.

The term d²θ/dt² is called angular acceleration. It has units of rad/s².


Since v_r and v_c are perpendicular to each other, the magnitude of the velocity of particle P is given by




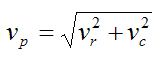
Since a_r and a_c are perpendicular to each other, the magnitude of the acceleration of particle P is given by





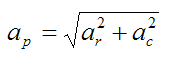
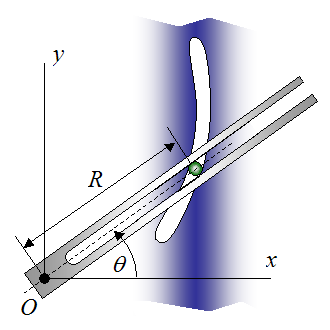
Example Problem For Curvilinear Motion

A slotted link is rotating about fixed pivot O with a counterclockwise angular velocity of 3 rad/s, and a clockwise angular acceleration of 2 rad/s². The movement of the link is causing a rod to slide along the curved channel, as shown. The radius of the channel as a function of θ is given by, R = 0.7θ (with R in meters and θ in radians). Determine the velocity and acceleration components of the rod at θ = 45°





Solution

The angle θ = 45° is equal to π/4 radians. In the equations, counterclockwise angular velocity is positive, and clockwise angular acceleration is negative (since it acts to “slow down” the rotational speed of the link).


The radial velocity of the rod is given by equation (1):



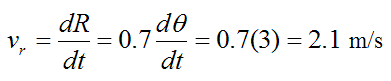
(The radial velocity is in the direction of increasing R).


The circumferential velocity of the rod is given by equation (3):



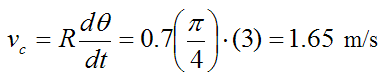
(The circumferential velocity is in the direction of increasing θ).


The radial acceleration of the rod is given by equation (2):



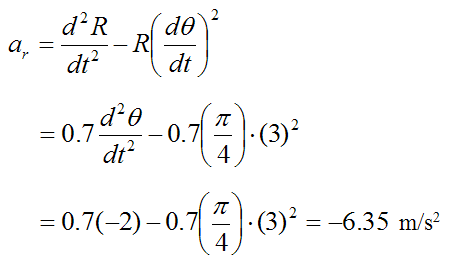
(The radial acceleration is in the direction of decreasing R).


The circumferential acceleration of the rod is given by equation (4):



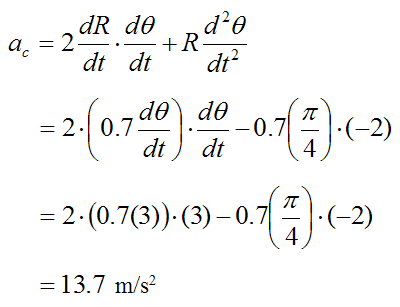
(The circumferential acceleration is in the direction of increasing θ).



Return to Kinematics page


Return to Real World Physics Problems home page