About me and why I created this physics website.

Rolling Without Slipping

Rolling without slipping commonly occurs when an object such as a wheel, cylinder, or ball rolls on a surface without any skidding.

To define such a motion we have to relate the translation of the object to its rotation.

For example, let’s consider a wheel (or cylinder) rolling on a flat horizontal surface, as shown below.



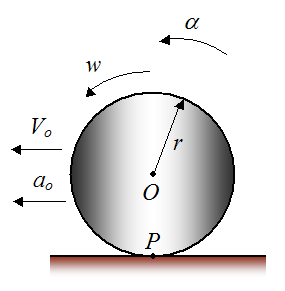
Where:

α is the angular acceleration of the wheel (in radians/s²), with respect to ground

w is the angular velocity of the wheel (in radians/s), with respect to ground

r is the radius of the wheel

V_o is the horizontal velocity of the geometric center O of the wheel, with respect to ground

a_o is the horizontal acceleration of the geometric center O of the wheel, with respect to ground

P is the contact point between wheel and surface


The wheel rolls without slipping only if there is no horizontal movement of the wheel at the contact point P (with respect to the surface/ground). Thus, the contact point P must also have zero horizontal movement (with respect to the surface/ground). This is analogous to a crate sitting stationary on the floor (i.e. it is not sliding). The crate has zero horizontal movement relative to the floor, and therefore the contact area of the crate (with the floor) also has zero horizontal movement (relative to the floor). For the case of the wheel, this is analogous to the contact point P having zero horizontal movement relative to the surface.

Now, if the wheel (shown above) were moving either right or left, but with no rotation, the wheel would skid along the surface. And as a result, the contact point P would also be moving either right or left.

Therefore, we deduce that the wheel must rotate (at a certain speed) for there to be no skidding on the surface.


To begin the analysis set up a schematic as shown below, along with sign convention.



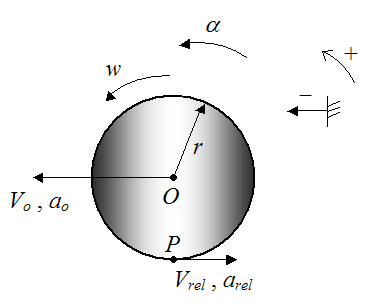
Where the following additional variables are introduced:

V_rel is the horizontal velocity of point P (on the wheel) relative to point O

a_rel is the horizontal acceleration of point P (on the wheel) relative to point O


Therefore, by vector addition the velocity of point P with respect to the surface/ground is:



Now, for rotational motion:



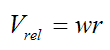
For no skidding V_p = 0. Therefore,



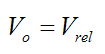
As a result,



For the case of rolling without slipping, this is the equation relating the velocity of the geometric center of the wheel O to the angular velocity w of the wheel.

If we differentiate the above equation with respect to time we get:



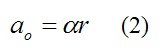
For the case of rolling without slipping, this is the equation relating the acceleration of the geometric center of the wheel O to the angular acceleration α of the wheel.

Equations (1) and (2) also apply for curved surfaces. In other words, even if the rolling surface were curved, the velocity of contact point P would still be zero for no slipping, and equations (1) and (2) would still apply. However, for a curved surface the velocity V_o is parallel to the tangent to the surface at the contact point P, and the acceleration a_o is parallel to the tangent to the surface at the contact point P. This is shown below.



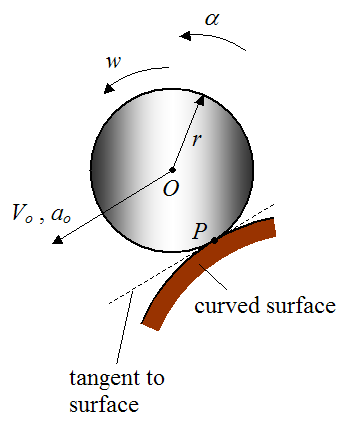
For many dynamics problems, rolling without slipping means there is a friction force acting on the wheel at the contact point P. This friction force prevents slipping. In this instance the friction is known as static friction since there is no relative sliding between the wheel and surface at the contact point P.


Rolling With Slipping

For the case of rolling with slipping, equations (1) and (2) do not apply, and there is no relationship between the velocity (and acceleration) of the geometric center O with the angular velocity (and angular acceleration) of the wheel. They are entirely independent of each other. In this instance there is relative sliding between the wheel and surface at the contact point P. This means there is a kinetic friction force acting on the wheel, at the contact point P.

To see examples of problems involving rolling (with and without slipping) see Physics Of Billiards, and Physics Of Bowling.



Return to Dynamics page


Return to Real World Physics Problems home page