About me and why I created this physics website.

Forces

The concept of forces is fundamental for solving statics and dynamics problems. If we know the forces that are acting on an object we can determine how it moves. Conversely, if we know how an object moves we can calculate the forces acting on it.

This latter point needs to be expanded on. In order to accurately determine the forces acting on an object we must know how the object is moving relative to an inertial reference frame. Equations of motion have been developed which relate the forces acting on an object to its motion (in particular, the acceleration), as measured from an inertial reference frame.

If the sum of the forces acting on an object is zero, then that object has zero acceleration relative to an inertial reference frame. Conversely, if the sum of the forces acting on an object is not zero, then that object is accelerating relative to an inertial reference frame.

The reverse is also true. If an object has zero acceleration relative to an inertial reference frame, the sum of the forces acting on that object is zero. Conversely, if an object is accelerating relative to an inertial reference frame, the sum of the forces acting on that object is not zero.

The fundamental nature of forces is broken down in Newton's Laws.


The force or forces acting on an object is always due to: (1) Contact with another object, and/or (2) A body force acting on it, such as gravity, or a magnetic field.

Forces are always depicted as vectors acting at some location on an object, as shown below (for example). The forces are given as: F₁, F₂,..., F_n.




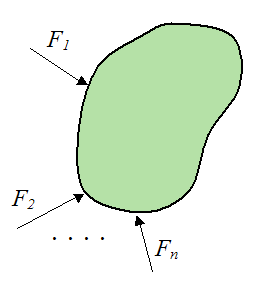
However, representing forces as vectors is merely a mathematical convenience for solving problems using the equations of motion.

But, forces don’t actually exist as vectors in real-world problems. To understand the reason for this we must look back at points (1) and (2), listed above.

When an object touches another object there is contact, not at an infinitely small point, but over an area of finite size. Thus, it is more suitable to speak in terms of a pressure that acts on the objects over the contact area. This pressure in turn, when multiplied by the contact area, gives the resultant force acting on each object. So, the force acting on an object (due to contact with another object) is actually a resultant force (based on pressure times area), which is commonly represented as a vector in the equations of motion. This is done for mathematical convenience.

For example, let’s say we have a man sitting on the edge of a crate. We represent his weight by a resultant force vector F (as shown).




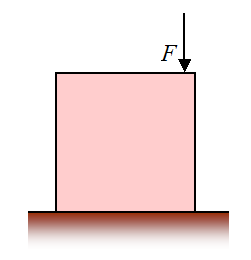
In addition, there is also a resultant contact force acting on the bottom of the crate (and pushing upwards) due to contact with the floor. As explained before, this resultant force is the result of a pressure that acts over the area in contact with the floor. The bottom of the crate is the contact area with the floor. Let's look more closely at this pressure distribution.

The pressure distribution acting on the bottom of the crate might look something like this:




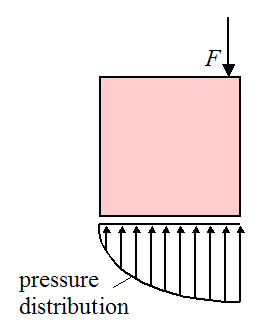
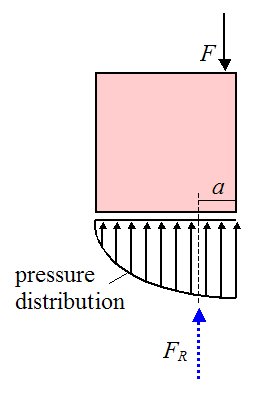
We can replace this pressure distribution with an equivalent resultant force (F_R) acting at a certain distance a from the right edge, as shown below:




To illustrate by way of example, let’s assume that the pressure distribution on the bottom of the crate only varies in the x-direction, as shown in the diagram below.




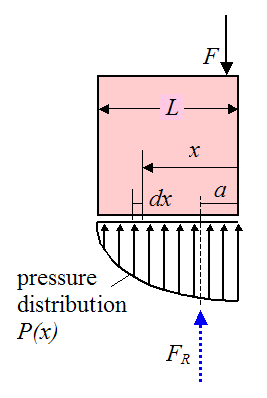
Assume that the width of the crate into the page is b, and that the length (along the x-direction) is L.

The resultant force F_R is calculated using integration over the contact area:



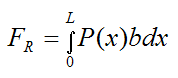
The distance a is the distance to the centroid of the pressure curve P(x). This is calculated using the following formula:




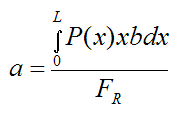
The resultant force F_R acting at distance a can replace the pressure distribution acting on the bottom of the crate, as shown below.




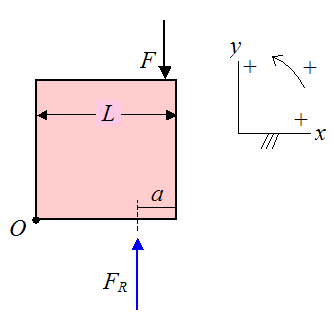
If we were to apply the equations of motion to the crate, the force F_R would be added to the force balance of the force equations, and the moment (caused by F_R) would be added to the moment balance of the moment equations. The moment (caused by F_R) is calculated knowing the magnitude of F_R and its line of action, which is at a distance a from the right edge. For example, let's take the moment of F_R about point O. Using the sign convention shown, this moment is equal to (L−a)F_R. This would be added to the moment balance of the moment equations.


Coming back to point (2) from before, if a body force such as gravity is acting on an object, the body force “pulls” equally on all the mass elements in it. For the sake of mathematical convenience, the total gravity force pulling on the entire body is also represented as a single resultant force vector acting at a certain location inside the object (and pointing in the direction of gravity). The location of this resultant gravity force (F_g) is at the center of mass G of the object, as shown below.




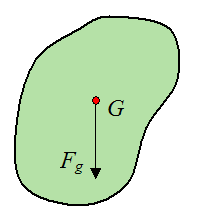
The magnitude of the vector F_g is equal to mg, where m is the mass of the object and g is the acceleration due to gravity.

Knowing the magnitude and direction of vector F_g, and the location of the center of mass G of the object, we can correctly account for it in the force and moment equations used for solving statics and dynamics problems.



Return to Dynamics page


Return to Real World Physics Problems home page