About me and why I created this physics website.

Projectile Motion

Projectile motion describes the motion of objects, which have the force of gravity and air resistance acting on them. In many problems, air resistance is neglected in the analysis. This is done to simplify the calculations.

The figure below shows the motion of a particle, under the influence of gravity only.



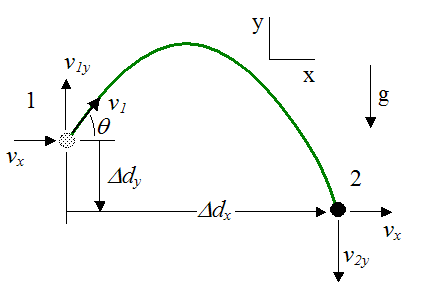
Define the following variables:

Δd_x is the change in horizontal position

v_x is the horizontal velocity (constant)

t is time

Δd_y is the change in vertical position

v_1y is the initial vertical velocity

g is the acceleration due to gravity, which on earth is 9.8 m/s²

v_2y is the final vertical velocity

v₁ is the initial launch velocity

θ is the initial launch angle, as shown


We are assuming no air resistance. So the particle travels exactly as it would while in a vacuum. Thus, we have the following equations describing the motion of a particle (projectile) in the absence of air resistance:





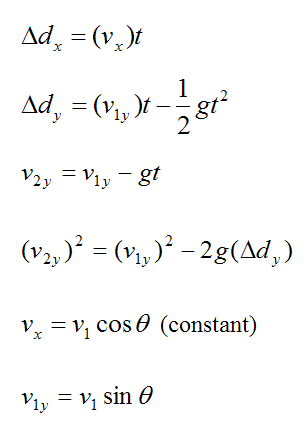
Note that the horizontal velocity v_x is treated here as constant because it is assumed there is no force acting on the particle in the horizontal direction, since air resistance is neglected. Therefore, only the vertical velocity of the particle changes since there is only a vertical (gravitational) force acting on the particle.

Note that the above equations are a direct result of applying the equations of rectilinear motion using constant vertical acceleration in the downward direction (g), and zero acceleration in the horizontal direction (since there is no force acting on the particle in the horizontal direction, since air resistance is neglected).


To see an interesting application of projectile motion go to The Physics Of Volleyball.


I created a simulator which accounts for the effect of air resistance for projectile motion problems. To find out more about this simulator see Projectile Motion Simulator.


If you want to test your understanding and solve some problems go to Projectile Motion Problems.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page