About me and why I created this physics website.

The Physics Of Jumping

In jumping events such as the long jump and high jump the athlete must propel him or herself into the air with as much speed as possible in order to achieve the maximum jump distance. In the high jump the jumping distance is the vertical distance that the athlete clears, and in the long jump the jumping distance is the horizontal distance that the athlete clears. In this page I will mainly discuss the physics of these jumping events.

The Physics Of Long Jump



Source: https://commons.wikimedia.org/wiki/File:2013_IPC_Athletics_World_Championships_-_26072013_-_Keng-Chin_Liang_of_Taipei_during_the_Men's_Long_jump_-_T12_2.jpg. Author: https://commons.wikimedia.org/wiki/User:Pleclown


In order to jump as far as possible in the long jump, the athlete must run as fast as he can and then jump up as high as he can at the point of takeoff. This is a case of projectile motion in which the maximum distance is achieved by maximizing horizontal velocity and vertical velocity at the point of takeoff. The figure below shows a schematic of the long jump.



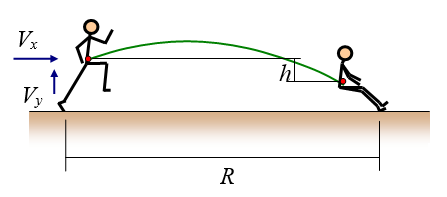
Where:

V_x is the horizontal velocity of the center of mass of the long jumper at the point of takeoff. The center of mass is represented by the red dot

V_y is the vertical velocity of the center of mass of the long jumper at the point of takeoff

h is the change in vertical position of the center of mass of the long jumper between the takeoff point and landing point

R is the horizontal jumping distance of the long jumper

The center of mass of the long jumper can be treated as a single particle obeying Newton's second law of motion. If we reasonably assume that air resistance is negligible, the motion of the center of mass of the long jumper is exactly predicted by the equations for projectile motion, during the airborne phase of the long jump. At the point of takeoff the horizontal velocity of the long jumper is already established (due to the speed build up during the run). So the only thing the long jumper can do at this point is maximize V_y in order to maximize R. This is achieved by pushing off the ground with the takeoff leg with as much force as he can. A greater V_y increases the time spent airborne which increases the jumping distance R.

To further maximize jumping distance, the long jumper can raise his legs so that he falls further down upon landing. This increases h and increases R as a result. Due to the importance of fast running speed in obtaining large long jump distance, it is no surprise that the best sprinters can also be the best long jumpers. Carl Lewis is a well known example of this.

A more elaborate jumping sport similar to the long jump is the triple jump in which athletes jump three times. Each of the three jump distances are maximized in a similar fashion to how a long jump distance is maximized. The video below shows a triple jump.




The Physics Of High Jump



Source: https://commons.wikimedia.org/wiki/File:Nicole_Forrester.JPG

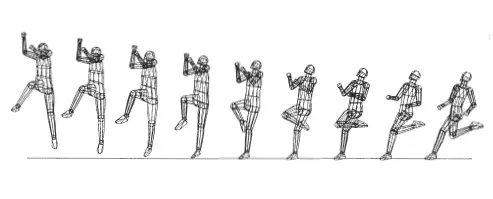
In order to jump as high as possible in the high jump (using the Fosbury Flop), the athlete must maximize his vertical jump velocity at the point of takeoff, while also having sufficient horizontal velocity to carry his body over the bar. Optimal high jump technique involves leaning back a bit and planting the takeoff leg ahead of the body, just before the jump. The figure below illustrates the run-up and takeoff for the high jump [1]. The high jumper must reach a fast running speed before takeoff. This enables him to maximize the vertical force exerted by his takeoff leg on the ground, which in turn helps maximize his vertical jump velocity [1]. The authors of [1] state: "When the takeoff leg is planted ahead of the body at the end of the run-up, the knee extensor muscles (quadriceps) resist against the flexion of the leg, but the leg is forced to flex anyway, because of the forward momentum of the jumper. In this process the takeoff leg's knee extensor muscles are stretched. It is believed that this stretching produces a stimulation of the muscles, which in turn allows the foot of the takeoff leg to press harder against the ground". This means that the takeoff leg (at the end of the run-up) pushes against the ground harder during takeoff than it would if the jumper is jumping from a standing position.

During the takeoff stage, the vertical range of motion of the center of mass of the high jumper must also be maximized in order to maximize the vertical takeoff velocity. This maximizes the time over which the takeoff force (exerted by the takeoff leg on the ground) is applied, which in turn maximizes the vertical takeoff velocity. So at the start of the takeoff stage the center of mass of the high jumper is in a low position and at the end of the takeoff stage it's in a high position. This is achieved by running with bent legs on the last few steps before takeoff and by running on a curve (which also lowers the center of mass of the high jumper due to the "lean" towards the center of the turn) [1].



In addition to the large takeoff force induced by planting the takeoff leg ahead of the body, there is additional physics to consider as a result of planting the takeoff leg. The takeoff foot, when planted, serves as a form of pivot enabling part of the horizontal momentum of the high jumper to be transformed into additional vertical (takeoff) momentum, which in turn translates into additional vertical takeoff velocity. The figure below shows a basic schematic of this, in which the high jumper is represented (for simplicity) as a thin rectangle. Stage (1) shows the high jumper before he leans back, near the end of the run. Stage (2) shows the high jumper after he leans back and just before he plants his takeoff leg in the ground. Stage (3) shows the high jumper just after he plants his takeoff leg in the ground. Angular momentum is conserved about pivot point P between stage (2) and (3). Treat this as a two-dimensional problem.



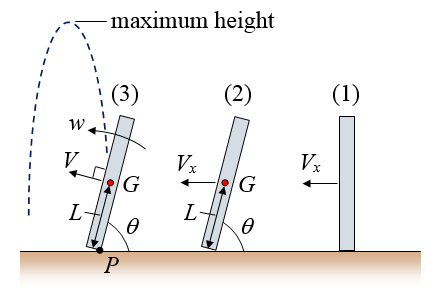
Where:

V_x is the horizontal velocity of the center of mass G of the high jumper just before he plants his takeoff leg in the ground

L is the distance between P and G

θ is the lean-back angle of the high jumper

V is the velocity of the center of mass of the high jumper just after the takeoff leg is planted in the ground. This is the velocity of the center of mass at the start of the takeoff stage.

w is the angular velocity of the high jumper just after the takeoff leg is planted in the ground

Since angular momentum is conserved about P we can write the following equation for conservation of angular momentum between stage (2) and (3), about P:

MV_xLsinθ = I_Pw         (1)

where M is the mass of the high jumper, and I_P is the moment of inertia of the high jumper about point P, about an axis pointing out of the page.

Now, w = V/L         (2)

Since the high jumper is represented by a thin rectangle,

I_P = (1/12)M(2L)²+ML²         (3)

Substitute equations (2) and (3) into (1) and solve for V. We get:

V = (3/4)V_xsinθ

The vertical component of V is V_y = (3/4)V_xsinθcosθ.

Note that this result assumes that the high jumper is a rigid body between stage (2) and (3), which is not completely accurate. But nonetheless, this result is informative and serves as a useful representation for part of the physics taking place during the takeoff stage.

As a rough estimate for elite level jumpers, use V_x = 8 m/s and θ = 70-80 degrees. This gives a vertical component V_y of 1-2 m/s (at the start of the takeoff stage). This vertical component V_y contributes to the vertical takeoff velocity of the high jumper (in addition to the contribution provided by the takeoff force generated by the takeoff leg). For example, if the vertical takeoff velocity of a high jumper's center of mass is 4.5 m/s (at the end of the takeoff stage) and the vertical component V_y is 1 m/s (at the start of the takeoff stage), then the takeoff force propels the high jumper upward at a certain acceleration such that the vertical velocity gain is 3.5 m/s between the start and end of the takeoff stage. The initial vertical velocity of 1-2 m/s can add significant height to the jump.

The center of mass of the high jumper can be treated as a single particle obeying Newton's second law of motion. If we reasonably assume that air resistance is negligible, the motion of the center of mass of the high jumper is exactly predicted by the equations for projectile motion, during the airborne phase of the high jump. Once the high jumper's feet leave the ground, the motion (and maximum height reached) of his center of mass is established and nothing more can be done by the high jumper to change it. However, once the high jumper is airborne he can further maximize the bar height he clears by bending his body around the bar using appropriate technique (as shown in the figure below). In doing so, his center of mass (the red dot) can actually pass underneath the bar, while enabling his body to pass over the bar (the black dot). This means that the bar can actually be placed higher than the maximum height reached by the center of mass of the high jumper.



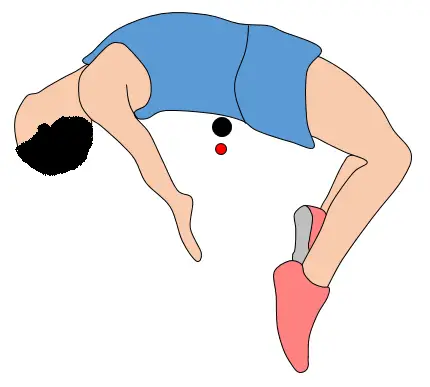
Lastly, the high jumper must have a slight rotational speed in order to go "around" the bar as he jumps over it. This rotational speed is established by the high jumper at takeoff, using the force exerted by his takeoff leg on the ground at takeoff.

This concludes the physics analysis of the long jump and high jump. For an interesting analysis involving standing jump height see Jump height on another planet.

Reference

1. J. Dapena and T.K. Ficklin, Scientific Services Project - High Jump (USA Track and Field), Biomechanics Laboratory, Dept. of Kinesiology, Indiana University, 2007. http://www.indiana.edu/~sportbm/High-Jump-Report-32-2007-Men-lodef.pdf



Return to The Physics Of Sports page


Return to Real World Physics Problems home page