About me and why I created this physics website.
The Physics Of Hitting A Baseball
Hitting the "sweet spot" is something that baseball players strive for. This is the location of the bat that is generally regarded as the best spot for hitting the ball. It minimizes vibration of the bat and results in the maximum energy delivered to the ball, meaning it travels the farthest.
The "sweet spot" is a special point on the bat which minimizes stinging of the hands when the ball strikes there. Baseball players say that hitting the ball in this location "feels" the best, and results in the most solid hit.
If the baseball strikes outside of the sweet spot a painful stinging sensation is felt in the hands, due to bat vibration. In addition, this undesirable vibration reduces the energy that is delivered to the ball, so it doesn't travel as far.
Here we are using physics to confirm what baseball players already know from experience.
It's not easy to hit the sweet spot. For best results, contact with the ball must be made within 1/8" of this special point. It is the main "good hit" criterion of players. But it is one of the biggest challenges in Major League sports, where a round ball traveling at 90 mph has to hit a round bat swinging at 80 mph, at precisely this location. The result is the ball flying off the bat at 110 mph, enough for a home run.
To find the sweet spot let's look more closely at the physics of the problem.
To simplify the analysis of the physics of hitting a baseball, let's assume the bat can be represented by a uniform slender rod, pivoted at the end. The reference frame and free body diagram for the slender rod is shown in the figure below.
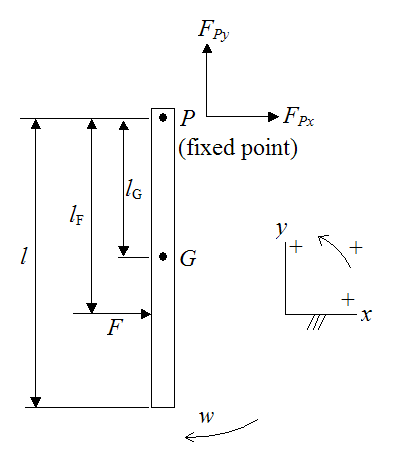
Where:
FPx is the x-component of the force exerted on the slender rod by the fixed pivot P. Note that P represents the hands of the hitter, holding on to the bat, and P is assumed to be a frictionless pivot.
FPy is the y-component of the force exerted on the slender rod by the fixed pivot P
G is the center of mass of the slender rod
F is the force exerted on the bat by the ball when it strikes
l is the length of the slender rod
lF is the distance from the point P to the contact point F
lG is the distance from the point P to the center of mass G
w is the angular velocity of the bat, in rad/s, just before it strikes the ball
We wish to find the distance lF given FPx = 0. This means that there will be no reaction force at P due to the force F.
This is a two-dimensional problem involving rigid body dynamics. To solve this type of problem in general we need one moment equation and two force equations (in the x,y direction).
The moment equation for rotation about a fixed point P is:
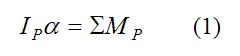
Where:
IP is the moment of inertia about P, about an axis pointing out of the page
α is the angular acceleration of the bat due to it "slowing down" when the ball strikes, in rad/s2
ΣMP is the sum of the moments about the fixed point P
The moment of inertia is calculated as:
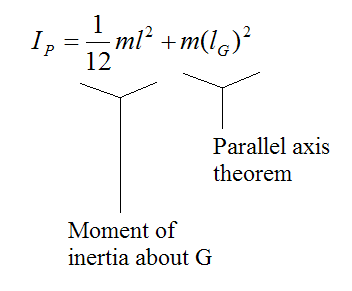
where m is the mass of the bat.
Now, since the slender rod is uniform along its length
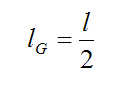
The sum of the moments (right-hand side of equation (1) ) can be expressed as:
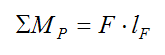
The angular acceleration α can be expressed as:
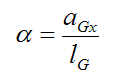
Where:
aGx is the linear acceleration of the center of mass of the bat in the x-direction due to it "slowing down" when the ball strikes
From Newton's Second Law, the force equation in the x-direction is:
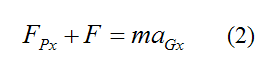
where FPx = 0
We don't need to account for the force equation in the y-direction. This is because the equations (1) and (2) by themselves allow us to solve the problem – since FPx = 0 we only have to solve for two unknowns: aGx and lF.
Solving, we get
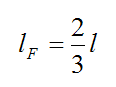
This means that the sweet spot is 2/3 of the distance along the rod, from the pivot P.
This result is interesting. It says that no matter how hard you hit the ball at this point, the reaction force FPx is always zero.
However, this particular solution is idealized. In a real bat the moment of inertia is significantly different from that of a uniform slender rod. Most of the weight is distributed near the end, and as a result lF is farther down than 2/3 of the bat length. This makes for a good design since the velocity of the bat is greater the farther we are away from P. This results in a harder hit.
In real bats, the location of the sweet spot is usually around 17 cm from the fat end of the bat.
However, the location of the sweet spot does not only depend on the mass and moment of inertia of the bat. It also depends on 1) where on the handle you're holding the bat, and 2) the size and mass of your hands. Since your hands move with the bat during the swing, they change the effective mass and moment of inertia of the bat. Thus, to best determine the location of the sweet spot according to the specific bat you use and conditions 1) and 2), you can do the following experiment, as shown in the figure below. Hold a bat and hit it at different locations along its length below the center of mass, using a rubber mallet. Hitting the bat below the center of mass but above the sweet spot will result in your hand being jolted to the left. Hitting the bat below the sweet spot will result in your hand being jolted to the right. When your hand remains steady and no longer "jolts" after each hit, you have found the sweet spot.
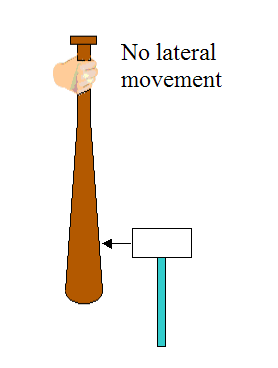
Note, if you were to hit the bat with the mallet on the other side of the bat (on the left), you would have the reverse situation, as follows: Hitting the bat below the center of mass but above the sweet spot will result in your hand being jolted to the right. Hitting the bat below the sweet spot will result in your hand being jolted to the left.
An intuitive explanation for the sweet spot is given as follows. When a force is applied to the bat, in general, the result is rotational and translational motion. So, referring to the figure above, applying a force F below the center of mass G results in a simultaneous counter-clockwise rotation and translational movement of the bat to the right. The rotational part of the motion causes the point P to move to the left. The translational part of the motion causes the point P to move to the right. The sweet spot is simply the unique point where these two contributions cancel each other out, resulting in the point P not moving.
The physics of baseball, in general, is a very interesting subject, and the physics of hitting a baseball, in particular, is a very involved area of study that calls upon a large amount of physics and engineering, especially when it comes to bat design, and the material used to make the bat (which is normally wood or aluminum).
Return to The Physics Of Sports page
Return to Real World Physics Problems home page