About me and why I created this physics website.

Newton's Laws Of Motion

Newton's Laws Of Motion – First Law

Newton's first law states that, if no net external force acts on a body at rest, that body will continue to remain at rest. If no net external force acts on a body moving in a straight line at constant velocity, that body will continue to move in a straight line at constant velocity.

Newton's Laws Of Motion – Second Law

Newton's second law states that, when a force acts on a particle, this force is equal to mass times acceleration.





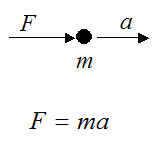
Where:

F is the force acting on the particle

m is the mass of the particle

a is the acceleration of the particle in the direction of the force, with respect to an inertial reference frame


We can also write the second of Newton's Laws for a system of particles:




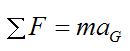
Where:

ΣF is the vector sum of the external forces acting on the system of particles. This sum is sometimes called the net external force

m is the total mass of the system of particles

a_G is the acceleration of the center of mass of the system of particles, with respect to an inertial reference frame. This acceleration is in the direction of the net external force


Note that there is no restriction in the way the particles are connected. As a result, the above equation will also hold true for a rigid body, a deforming body, a liquid, or a gas system.

For proof of the above equation see Newton's Second Law.


Newton's Laws Of Motion – Third Law

Newton's third law states that, for every action there is an equal and opposite reaction. This means that, when two bodies are in contact, the reactions between those bodies are equal in magnitude and opposite in direction. The figure below shows an example of two bodies in contact.





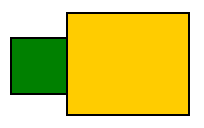
If we were to isolate each body, the reactions acting on them will be equal and opposite. The figure below shows a general example of the reactions acting on each body.





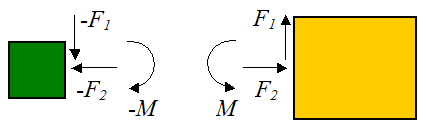
where F₁ is the resultant vertical force, F₂ is the resultant horizontal force, and M is the resultant moment (torque) at the contact surface.

The resultant vertical force acting on each body is the sum of all the forces acting in the vertical direction, along the contact surface.

The resultant horizontal force acting on each body is the sum of all the forces acting in the horizontal direction, along the contact surface.

The resultant moment (torque) acting on each body is the sum of all the torques, along the contact surface. The torques are caused by equal forces acting in opposite directions. For example, the figure below shows equal forces F_c , acting in opposite directions (on each of the bodies), and separated by a perpendicular distance R apart.





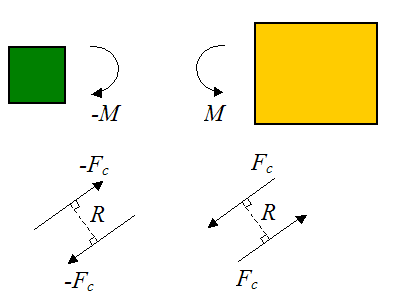
From this, the moment (torque) is calculated as:




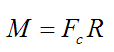
The moment M causes pure rotation of the body. It is not included in the force balance in Newton's second law (F = ma), since the forces F_c cancel out. Instead, it is included in the moment balance when applying the moment equations (see Rigid Body Dynamics).

In general, when solving real world physics problems, every contact surface (or contact point) between one body and another body can be replaced with a single resultant force F (which can be resolved into its components; such as horizontal and vertical, as shown above), and a moment M. And this force and moment will be equal in magnitude and opposite in direction on each of the bodies.

Note that for some cases, there will only be a resultant force F or resultant moment M acting on the contact surface. However, it may not be obvious which one it is. So instead, one must work it out by way of calculation (by solving dynamics equations).

For example, a lubricated ball and socket joint cannot resist twisting, so it has no moment M. But it will resist pushing and pulling, so it will have a resultant force F acting at the contact surface (between ball and socket). On the other hand, some contact surfaces only have a resultant moment M acting (pure twisting). An example of this is the handle of a screwdriver.

The main advantage of replacing a contact surface (or contact point) with a single resultant force F and a single resultant moment M is mathematical convenience. It allows for the dynamics equations to be solved in as straightforward a manner as possible.

Another way to look at it is as follows: The general motion of a body always consists of translation and rotation. The resultant forces F acting on the body, contribute to translation and (depending on where the forces act), rotation as well. The resultant moments M acting on the body, contribute only to pure rotation. This is why forces are generally accounted for in both the force equations (F = ma), and moment equations. But moments are only accounted for in the moment equations. For an example of this, see Physics Of A Golf Swing.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page