About me and why I created this physics website.
The Physics Of A Golf Swing
The physics of a golf swing is deceptively more complicated than one might imagine. At first glance it might appear as simple as swinging a club and hitting the ball. But in fact, there is quite a bit more to it. There is the importance of technique obviously, but there is also some interesting physics that goes into making the "perfect" golf shot.
There are two main components that go into golf swing physics. Both these will result in the best possible shot:
1. Good swinging speed of the arms and shoulders.
2. Uncocking the wrists at the right moment so that the club connects squarely with the ball. Uncocking the wrists means letting the wrists rotate freely, while still holding on to the club.
The importance of the first point is fairly obvious. You must generate good swing speed to hit the ball hard enough, so that it goes far.
The second point is not as obvious. To understand the physics of a golf swing one must consider the mechanics of rotational motion. When an object travels around in a circle it moves outward, if unconstrained. To visualize this, imagine yourself sitting in a car that makes a sharp left turn. If you're not wearing your seat belt you'll go sliding across the seat towards the right, due to the effects of centripetal acceleration.
Similarly, by uncocking your wrists during the golf swing, the club will move radially outward (since it's not restrained). This is unlike, say, baseball where the batter "drives" the bat through its arc using raw muscle power. A baseball player relies on strong wrists and forearms to get a solid hit. His hands are "active". This is unlike golf, where the players hands are "passive" since they exert no twisting force on the club. This probably gives you some idea why baseball players have such beefy forearms and wrists. They need the strength to power the bat through the swing.
Uncocking the wrists allows the golf club to "straighten out", and in the process gain additional speed which translates into a harder hit than if the golf club were held rigid (meaning the wrists are not allowed to rotate during the swing).
The figure below shows a strobe picture taken of Bobby Jones golf swing, in the 1940s (source: http://www.clubmaker-online.com/bj003.gif).
In this picture, you can see the physics in action. At the top part of the swing, the golf club remains at a fixed angle relative to his arms (since his wrists are cocked). But in the bottom part of the swing, the golf club begins to "release" and the angle between it and his arms begins to rapidly increase (since his wrists are now uncocked), and the club moves radially outwards as a result. At the bottom of the swing the golf club is almost perfectly parallel to his arms. This is where contact is made with the ball.
Part of the physics of a golf swing (from the point of view of the golfer), means finding the release (wrist uncocking) point so that at the bottom position, where the players hands are directly above the ball, the golf club is in the vertical position parallel to his arms. This will maximize the speed of the club head upon impact, and result in the farthest hit.
Once the player knows the approximate point in the swing where he can uncock (release) his wrists, he just has to practice it over and over until it becomes second nature. And prior to this release point he just has to keep his wrists cocked; meaning, maintain his grip in a fixed position so that the club maintains a constant angle with his arms. Once he releases his wrists the physics takes care of the rest, and the club will move radially outwards due to the effect of centripetal acceleration.
Fortunately, using proper analysis, we can help reduce the trial and error for a golfer, who wishes to perfect his swing. The physics can thus be modeled as a dynamics problem, which will allow us to predict the approximate release point for the wrists. This analysis won't exactly capture every nuance of the golf swing, but will be rich enough in detail so that a golfer can enhance his or her understanding, and if they are a beginner, reduce some of the learning time that goes into perfecting the swing.
Physics Of A Golf Swing – Analysis
To begin the analysis let's look at the strobe picture of Bobby Jones swing once more. To better illustrate the motion, I drew a red curve and blue curve. The red curve traces the motion of his hands at the grip location, throughout the swing. The blue curve traces the motion of the club head throughout the swing. The red curve is almost a perfect circle, as you can see. The blue curve is not a circle, but is spiral shaped. The largest radius of the (blue) curve occurs at the bottom of the swing, where the club is fully extended.
Now that we have a clearer picture of the motion involved, we can draw a schematic of the set up. Note that the physics behind the swing will be treated here as a two-dimensional problem.
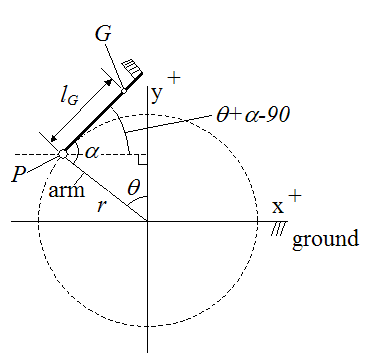
Where:
r is the radius of the golfer's swing
P is the grip location where the golfer is holding on to the club
G is the center of mass of the golf club
lG is the distance from P to the center of mass of the golf club
θ is the swing angle the golfer's arms make with the vertical
α is the angle the golf club makes with the golfer's arms
Next, we need to draw a free-body diagram of the golf club. This is the important object of study since it is the golf club that is reacting to "input" from the golfer, so it must be isolated from the system.
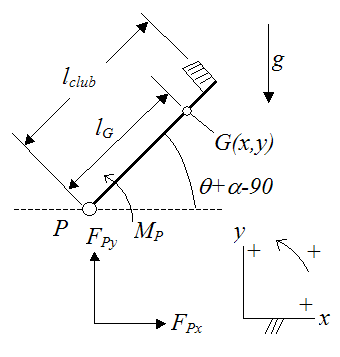
Where:
g is gravity, acting downwards. This value is equal to 9.8 m/s2
lclub is the length of the club
MP is the moment exerted on the golf club at P by the players hands
FPx is the horizontal force exerted on the golf club at P by the players hands
FPy is the vertical force exerted on the golf club at P by the players hands
G(x,y) is the position, in Cartesian coordinates, of the center of mass G. Note that this position is with respect to ground, and is a function of time.
We can express the position of the center of mass as follows:
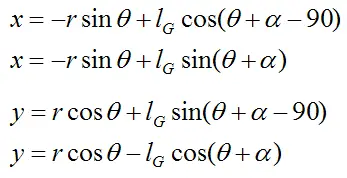
Next, using Newton's Second Law we write the general force equation in the x-direction:
Where:
ΣFx is the sum of the forces in the x-direction
m is the mass of the golf club
aGx is the acceleration of the center of mass in the x-direction, with respect to ground
Note that
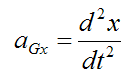
Thus we have
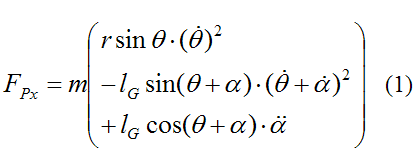
For simplicity, note the following notation:
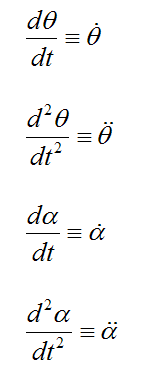
For simplicity, it is also assumed that the golfer's arms rotate at a constant angular velocity. In other words, the angular acceleration is zero:
Similarly, by Newton's Second Law the general force equation in the y-direction is:
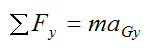
where ΣFy is the sum of the forces in the y-direction, and aGy is the acceleration of the center of mass in the y-direction, with respect to ground.
Note that
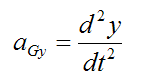
Thus we have
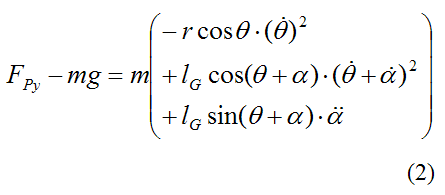
We must now write the general moment equation for rotation of a rigid body about its center of mass G.
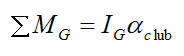
Where:
ΣMG is the sum of the moments about the center of mass
IG is the moment of inertia of the golf club about its center of mass, about an axis pointing out of the page
αclub is the angular acceleration of the club
Note that
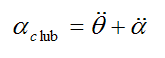
This is the angular acceleration of the golf club with respect to ground.
Thus, the moment equation becomes
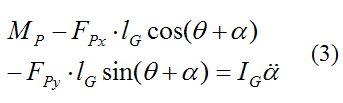
To solve these equations we can substitute (1) and (2) into (3). The resulting equation is as follows:
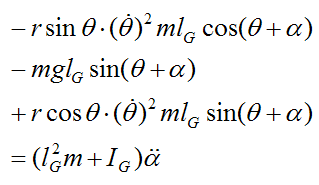
This is a second order differential equation in terms of α. It can only be solved numerically. It will solved for the part of the swing where the wrists are uncocked, and subject to the following initial conditions at the release point, given as:
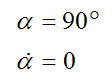
Note that α = 90° is a common (and approximate) angle that golfer's hold the club relative to their arms, prior to uncocking their wrists.
An additional condition is that MP = 0 since the wrists are allowed to rotate freely at the release point, and at every point in the swing thereafter.
The other unknown quantities in the equation such as r, m, lG, IG are constants based on the properties of the golf club and the parameters of the golfer's swing.
Using trial and error, one must input different wrist uncocking (release) angles, in the above equation (for θo), until α = 180° at θ = 180° (in the solution).
Physics Of A Golf Swing – Solution
This graph shows a representative solution which gives good insight into how the golf club angle α increases as the swing angle θ increases.
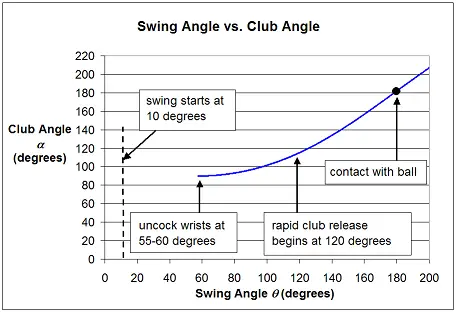
For the above solution shown in the graph, I chose the following input values which I feel are fairly representative of the typical golf club and golf swing:
lG = 0.58 m
IG = 0.015 kg-m2
m = 0.300 kg
r = 0.5 m
dθ/dt = 15 rad/s
Initial swing angle θoi (at start of swing) = 10°
Swing angle θo (just before release) = 57°
Initial club angle α (just before release) = 90°
So according to this particular model, the optimal release angle to uncock your wrists is θo = 55-60° .
Closing Remarks
It is interesting to see that the most rapid increase of club angle α (shown in the graph above) begins at a swing angle of around θ = 120° (even though uncocking of the wrists occurs much earlier in the swing). This is because the club angle α increases slowly at first before reaching a rapid release rate. However, looking at the strobe picture of Bobby Jones' swing one might (mistakenly) conclude that the correct swing angle to uncock your wrists is at approximately 120°, simply because that is when the increase in club angle α becomes very noticeable. Thus, analyzing the physics of a golf swing using a dynamics approach, will yield more accurate information than if someone were to just observe a golfer's swing, and draw conclusions from that. The lesson here is that certain information can only come to the surface when the physics of the problem is examined carefully.
A final consideration is to see how fast the club head moves at the point of impact, at the bottom position (using the previous input values). Since the club head is moving horizontally (in the x-direction) at the bottom position, there is no vertical component of velocity (in the y-direction). Therefore, the velocity of the club head is given as:
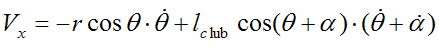
Note, the above equation is derived by calculating dx/dt, and replacing lG with lclub.
Using a club length lclub = 0.7 m, r = 0.5 m, θ = α = 180°, dθ/dt = 15 rad/s, and dα/dt = 19 rad/s (as calculated from the solution), we get Vx = 31 m/s for the club head speed just before it hits the ball.
It is interesting that, in analyzing the physics, we see that the arms and wrists play a somewhat passive role, and yet a powerful hit results. So where does the swing energy come from? It comes from the muscles in the torso and shoulders which swiftly rotate the golfer's arms and club through the swing. Uncocking the wrists at the optimal swing angle means that, as much energy as possible is transferred to the club head (in the form of kinetic energy), just before it contacts the ball.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page