About me and why I created this physics website.
Kinematics Problems
On this page I put together a collection of kinematics problems to help you understand kinematics better. The required equations and background reading to solve these problems is given on the kinematics page.Problem # 1
A car accelerates from rest at 4 m/s2. What is the velocity of the car after 4 seconds? (Answer: 16 m/s)
Problem # 2
What is the distance traveled by the car in Problem # 1, in 3 seconds? (Answer: 18 m)
Problem # 3
After 4 seconds, the car in Problem # 1 applies the brakes and comes to a full stop after 2 seconds. What is the acceleration of the car and what is the braking distance? (Answer: -8 m/s2, 16 m)
Problem # 4
A slotted link is rotating about fixed pivot O with a counterclockwise angular velocity of 3 rad/s, and a clockwise angular acceleration of 2 rad/s2. The movement of the link is causing a rod to slide along the curved channel, as shown. The radius of the channel as a function of θ is given by, R = 0.7θ (with R in meters and θ in radians). Determine the radial and circumferential velocity and acceleration components of the rod at θ = 45° . (For the answer see the curvilinear motion page, and scroll to the bottom of the page)
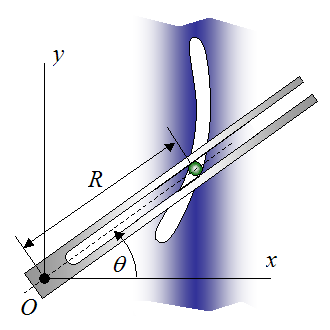
Problem # 5
Find the velocity of point B in the crank mechanism if the velocity of point A is vA, in the direction shown. The information is given in the figure. (For the answer see the instant center page, and scroll down to the example problem for Case 1)
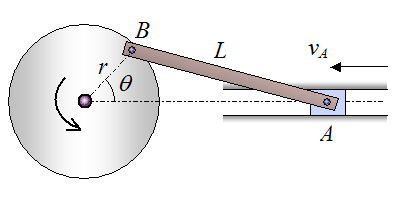
Problem # 6
The figure below shows a gyro top experiencing a state of general motion. The motion is such that the vectors wn and αn are always in the XY plane, and the vectors wp and αp are always in the Z-direction. Note that w is the angular velocity and α is the angular acceleration.
At the instant shown, determine the angular velocity and angular acceleration of the gyroscope wheel. Also, determine the velocity and acceleration of point A on the wheel. (For the answer see the gyro top page)
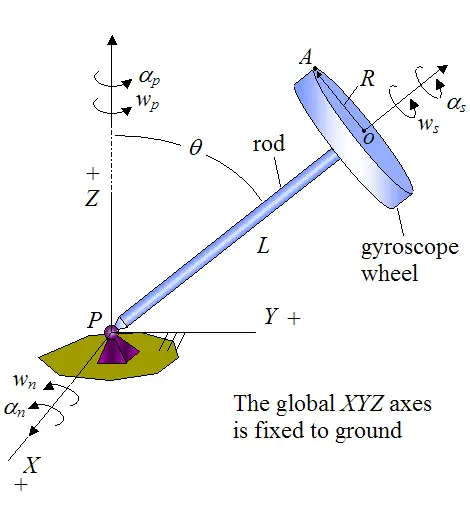
Problem # 7
What percentage of the total hang time does a basketball player spend in the highest 25% of the jump? (For the answer see the physics of basketball page)
Problem # 8
A linkage arrangement is shown below. The pin joints O1 and O2 are attached to a stationary base and are separated by a distance b. The linkages of identical color have the same length. All linkages are pin jointed and allow for rotation. Determine the path traced by the end point P as the blue linkage of length b rotates back and forth. (Answer: The path is a straight line)
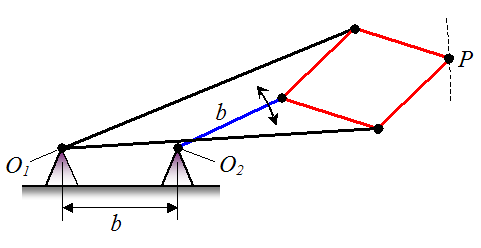
Problem # 9
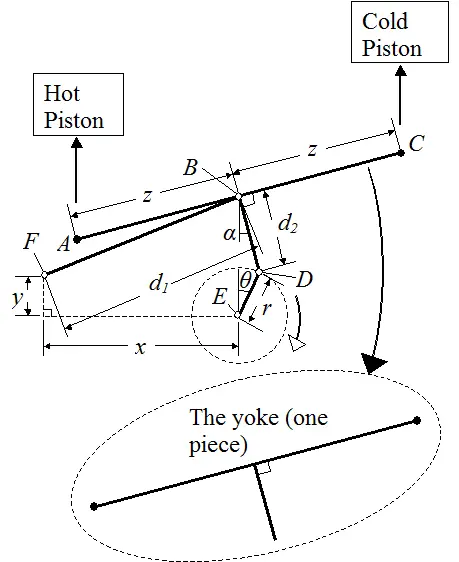
A Ross Yoke is commonly used as the drive mechanism for Stirling engines. The figure below shows a Ross Yoke mechanism, with variables shown. The pistons of the Stirling engine are attached to A and C and reciprocate up and down as the flywheel rotates around an angle θ. Point A is connected to the hot side piston, and Point C is connected to the cold side piston.
Points B and D are pin joints which allow for rotation and translational motion. Points E and F are pin joints which are fixed in place - they only allow for rotation. Determine the mathematical equation which relates the angles α and θ.
(Answer: d12 = (x + rsinθ − d2sinα)2 + (rcosθ + d2cosα − y)2 )
Problem # 10
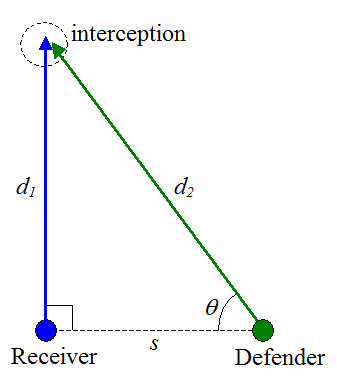
In a football game the defender is running to intercept the receiver. It is given that this is a kinematics problem in which both players are experiencing uniform motion. The receiver is running at 7 m/s. The blue and green dots represent the initial positions of the players. The angle θ represents the running trajectory of the defender, as shown, and s is the initial distance between the two players. At what velocity must the defender run at in order to intercept the receiver, as shown in the figure below? What is the distance traveled by the receiver (d1) and the defender (d2)? (Answer: 7/sinθ, stanθ, s/cosθ)
For more kinematics problems see:
acceleration problems
circular motion problems
free fall problems
projectile motion problems
relative velocity problems
uniform motion problems
velocity problems
Return to Physics Questions page
Return to Real World Physics Problems home page