About me and why I created this physics website.

Instant Center

For rigid bodies experiencing general plane motion (in two-dimensions), the concept of instant center allows one to conveniently calculate the unknown angular velocity of the rigid body, or unknown linear velocities of points on the rigid body. The instant center is an imaginary point that allows for a mathematical “shortcut” in calculating these unknowns.

The instant center is also called the instantaneous center of zero velocity (IC). It lies on an imaginary axis of zero velocity, about which the body appears to rotate at a given instant. This axis is always perpendicular to the plane of motion.

There are three basic cases to consider when solving problems using the instant center approach.



Case 1 – Consider a rigid body rotating in a plane. We wish to determine the velocity of a point A on the rigid body given the known velocity of another point B on the rigid body. The directions of the velocities are known and they are nonparallel. The figure below illustrates the set up of the problem.



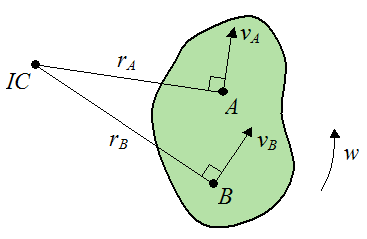
Where:

v_A is the velocity of point A, at the instant shown

v_B is the velocity of point B, at the instant shown

IC is the intersection of the lines r_A and r_B

r_A is the distance from the IC to point A, at the instant shown. This distance is drawn as perpendicular to the velocity v_A

r_B is the distance from the IC to point B, at the instant shown. This distance is drawn as perpendicular to the velocity v_B

w is the angular velocity of the rigid body, at the instant shown


The distances r_A and r_B are generally determined from the geometry of the rigid body, and trigonometry.

Note that the lines r_A and r_B are drawn in the direction that will result in them converging to a point (the instant center IC).

Also note that the direction of the velocities v_A and v_B correspond to the direction of rotation of the rigid body.


The velocity of point A is given by



The velocity of point B is given by



Combine equations (1) and (2) to eliminate the variable w, and we get




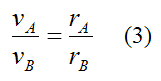
Equations (1), (2), and (3) can be used to solve for any two unknowns in the equations, with the remaining variables known.


Example Problem for Case 1

Find the velocity of point B in the crank mechanism if the velocity of point A is v_A, in the direction shown. The information is given in the figure.




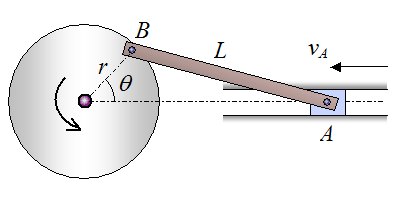
Solution

Set up the solution as drawn below, with new variables introduced as shown. The line r_A is drawn as perpendicular to velocity v_A. The line r_B is drawn as an extension of the line passing through point O and point B.

Point B traces a circle during the motion of the crankshaft. By geometry, the velocity v_B is tangent to this circle at point B. Also by geometry, the line r_B is perpendicular to the velocity v_B.




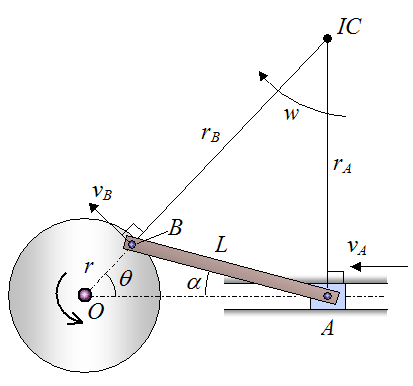
By geometry, the distance OA is given by



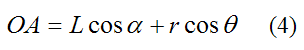
Also,



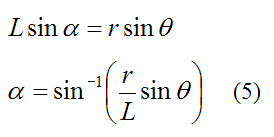
Substitute equation (5) into equation (4) and we get




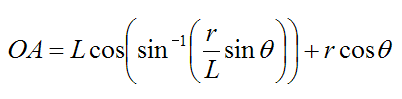
The points O, A, and IC form a right-angled triangle. Therefore we can use trigonometry to solve for r_A and r_B:




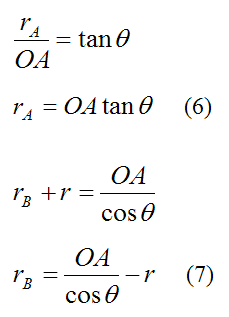
With v_A known, substitute equations (6) and (7) into equation (3), to solve for the velocity of point B (V_B).

Therefore,




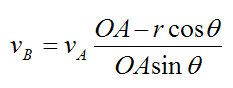
Note that when θ = 0, V_B = ∞. This is because r_A = 0 and as a result equation (3) can no longer be used. The angle θ = 0 is an example of a degenerate case where the instant center approach cannot be used to solve the problem.


For Case 1, a special case exists where the velocities at points A and B are pointing in the same direction (parallel), and the line passing through points A and B is not perpendicular to the direction of these velocities. For this case, the lines r_A and r_B are parallel and do not intersect. This means that r_A and r_B are infinitely long, and the IC lies at infinity. As a result, w = 0 and all the particles in the rigid body have the same velocity (i.e. the magnitude of the velocities and the direction of the velocities of all the particles in the rigid body are the same).



Case 2 – Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem.




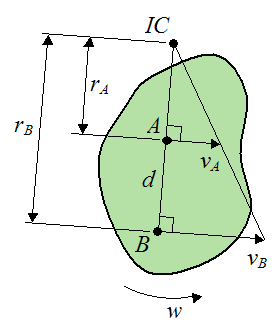
Note that IC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors v_A and v_B.

The distance between points A and B is d.


By similar triangles:



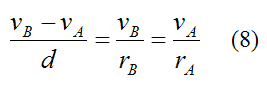
The velocity of point A is given by



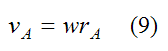
The velocity of point B is given by



Combining equations (8)-(10), it follows that the angular velocity is




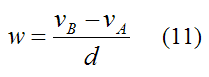
Example Problem for Case 2

A wheel of radius R has velocities as shown at points A and B. Determine the angular velocity of the wheel.




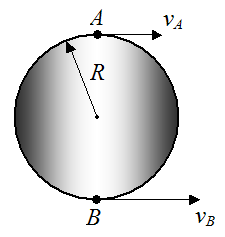
Solution

The distance between points A and B is 2R. From equation (11) the angular velocity is





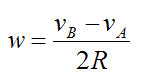
Case 3 – Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are pointing in parallel, but opposite directions. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem.




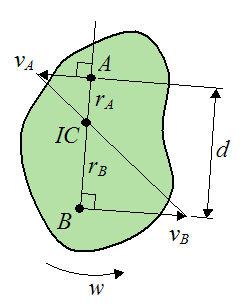
Note that IC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors v_A and v_B. Unlike the previous case, the IC lies in between points A and B.

The distance between points A and B is d.


By similar triangles:



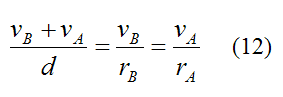
The velocity of point A is given by



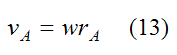
The velocity of point B is given by



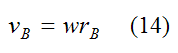
Combining equations (12)-(14), it follows that the angular velocity is




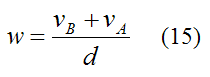
Example Problem for Case 3

A wheel of radius R has velocities as shown at points A and B. Determine the angular velocity of the wheel.




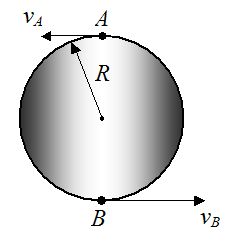
Solution

The distance between points A and B is 2R. From equation (15) the angular velocity is




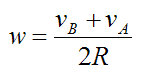
In Closing

Note that the spatial location of the instant center can change with time. So in general its use only applies at the instant considered, which corresponds to the information given in the problem, at the instant considered. In general, if the velocities of points A and B change, and/or their directions change, a new instant center must be calculated to solve for the (new) unknown linear velocities, or angular velocities.

In general, the instant center approach should not be used for finding the acceleration of points in a rigid body. This is because the instant center (IC) does not generally have zero acceleration.



Return to Kinematics page


Return to Real World Physics Problems home page