About me and why I created this physics website.

Vector Derivative

Finding a vector derivative may sound a bit strange, but it’s a convenient way of calculating quantities relevant to kinematics and dynamics problems (such as rigid body motion).

The standard rules of Calculus apply for vector derivatives. It’s just that there is also a physical interpretation that must go along with it.

One of the most common examples of a vector derivative is angular acceleration, which is the derivative of the angular velocity vector. In other words, the angular acceleration vector is the rate of change of the angular velocity vector.

To help you visualize this, consider the figure below showing an angular velocity vector (w) and an angular acceleration vector (α). In general, these two vectors point in different directions in three-dimensional problems.




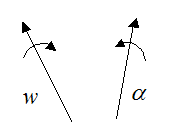
We can express w and α as their vector components:




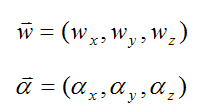
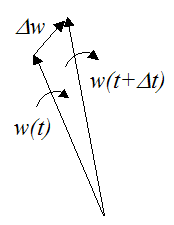
To calculate the angular acceleration vector, we calculate the difference in the angular velocity vector over a very small time step Δt, where Δt→0. To illustrate, see the figure below.



Using calculus, the angular acceleration is calculated by taking the limit as Δt→0, where



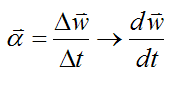
That’s all there is to it!

Now, there are situations (especially in two-dimensional problems) where it is not necessary to take the derivative of a vector, and the problem can be solved using techniques that are perhaps more familiar to the student.

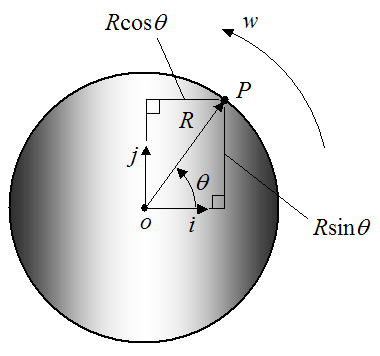
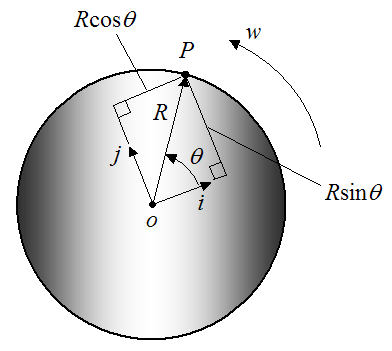
This is illustrated with the following example. Let’s say a wheel of radius R is rotating about a fixed point o, with a counterclockwise angular velocity w, as shown below. We wish to find the velocity of point P on the wheel (v_p).




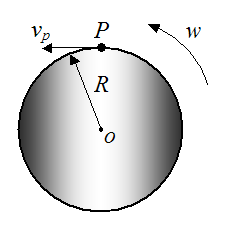
To solve this problem we can express the position of the point P in terms of polar coordinates (R,θ). This will allow us to determine the velocity of point P.

For the point P defined in polar coordinates (as shown below), we can derive a general equation for its velocity.



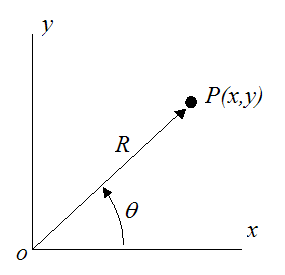
We set up the position of the particle P with respect to time, where



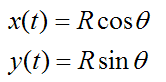
To find the velocity, take the first derivative of x(t) and y(t) with respect to time:




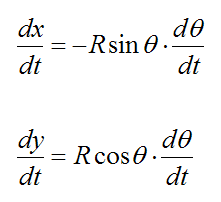
Since dθ/dt = w we can write




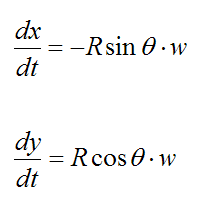
The point P corresponds to θ = 90° . Therefore,




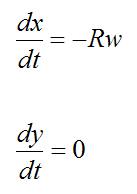
The velocity of point P is therefore




If we want to use the vector derivative approach to solve for the velocity of point P, we can do the following.

Set




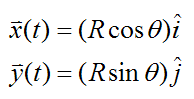
where i and j are defined as unit vectors pointing along the positive x and y axes (respectively), at the given instant. The unit vectors i and j are also defined as attached to the wheel and rotating with it. This means that the point P does not move relative to the unit vectors i and j. As a result, the terms Rcosθ and Rsinθ are constant in the above two equations. To understand this consider the following illustration which shows the position of the wheel at two consecutive instants:


Instant 1




Instant 2




As you can see, between instants 1 and 2 the position of point P does not move relative to the unit vectors i and j.

We are now ready to differentiate the above two equations with respect to time:




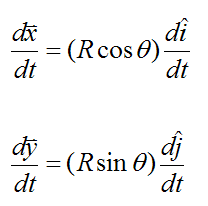
At the given instant, the velocity at point P is given by setting θ = 90° in the above equations. This gives us



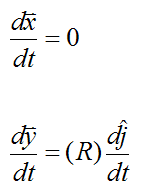
The term dj/dt is determined by examining how the unit vector j changes direction at the given instant, due to rotation w. This is illustrated in the figure below.




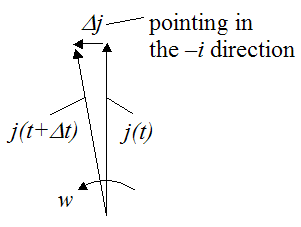
Using calculus, and taking the limit as Δt→0:



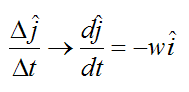
Therefore,



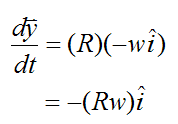
As a result,



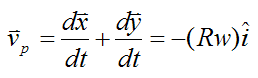
This is the same answer as before.


However, even though both approaches work, for three-dimensional kinematics and dynamics problems it is generally easier to evaluate vector derivatives, since that tends to make the solution as simple as possible (this becomes evident as one works through problems involving three-dimensional motion). In addition, equations have been specifically developed for rigid body motion, which involve vector derivatives. To see these equations click here.


The Derivative Of An Arbitrary Vector Of Fixed Length

Using the understanding gained thus far, we can derive a formula for the derivative of an arbitrary vector of fixed length in three-dimensional space.

Consider the figure below.



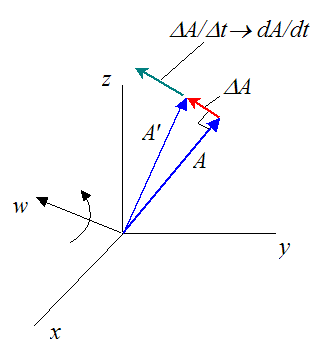
Where:

A is an arbitrary vector

A' is vector A rotated to a new orientation an infinitesimally short time later (Δt→0)

ΔA is the difference between vector A' and vector A (as Δt→0)

w is the angular velocity which "rotates" vector A (this is also a vector)


We wish to find an expression for dA/dt at the given instant.


Since the vector A is physically "rotating" due to w, then (as a result) vector dA/dt is perpendicular to A and w.

We can write:



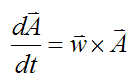
Hence, using the vector cross product we have a very useful formula relating the derivative of a vector of fixed length to the angular velocity that "rotates" this vector, in three-dimensional space. Note that the above formula also applies if vector A is translating as well as rotating. This means that only a rotation w can change the orientation of a vector of fixed length.


The Derivative Of An Arbitrary Vector Of Changing Length

Using the previous result we can derive a general formula for the derivative of an arbitrary vector of changing length in three-dimensional space.

First, set



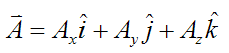
where A_x, A_y, and A_z are the components of the vector A along the xyz axes, and i, j, k are unit vectors pointing along the positive x, y, z axis (respectively). These unit vectors are defined as moving with the vector A.

Now, take the vector derivative of A with respect to time. This gives us



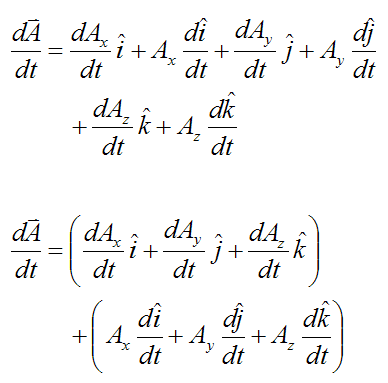
Since i, j, k are unit vectors of fixed length we can use the result from the previous section and write



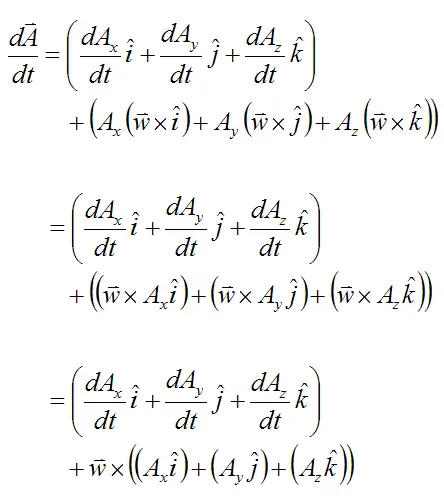
As a result,



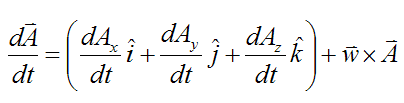
This formula reduces to the formula given in the previous section if A is of fixed magnitude (length), since dA_x/dt, dA_y/dt, dA_z/dt all equal zero. But if A changes length then dA_x/dt, dA_y/dt, dA_z/dt do not all equal zero.

The physical interpretation of dA_x/dt, dA_y/dt, dA_z/dt is that they are the rate of change of A_x, A_y, and A_z relative to the unit vectors i, j, k (which are moving with vector A). So, if there was an observer "attached" to these unit vectors (and moving with them), the terms dA_x/dt, dA_y/dt, dA_z/dt would be the rate of change he observes.


By now it should be more clear on why a vector derivative can be very useful. Fundamentally it's the same as a regular derivative, but with a physical interpretation included.



Return to Kinematics page


Return to Real World Physics Problems home page