About me and why I created this physics website.
The Physics Of Tennis
Source: https://commons.wikimedia.org/wiki/File:Tommy_Haas_serves.jpg. Author: https://commons.wikimedia.org/wiki/User:DianeAnna
Tennis is a game of strategy, strength, and fast reflexes. Success in the game largely comes down to how the racket is wielded. It's not simply a matter of hitting the ball with the racket, but which spot on the racket is used to hit the ball. Depending on whether the ball is stationary or coming at you, there are different spots on the racket which are best suited to strike the ball. In this page I'm going to present some mathematics which is only necessary insofar as understanding where the results come from; results which give a clear indication of where to hit the ball depending on whether it's stationary (during a serve) or coming at you after being hit by the other player.
A tennis racket can be approximately modeled as an object that is suspended from a fixed point on the handle, about which the racket can freely pivot. This pivot point represents the player's hand. The tennis ball hits the racket at a right angle, at some point along its length, which results in a dynamic reaction between racket and ball, which we wish to explore. Ball spin, if present, is assumed to have a negligible effect. This will be treated as a two-dimensional problem. The figure below shows a schematic of the tennis racket, with sign convention shown.
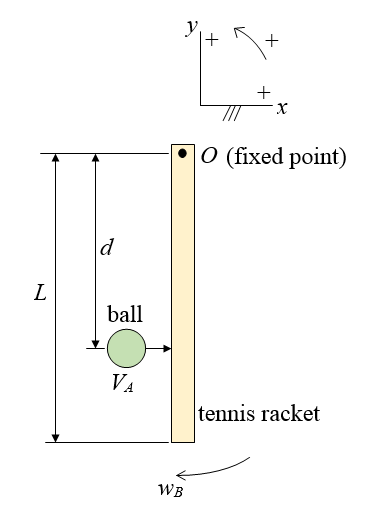
Where:
L is the length of the racket, measured from the fixed pivot point O to the end of the racket
d is the distance, measured from point O, to where the ball impacts the racket
VA is the velocity of the ball, just before it impacts the racket
wB is the angular velocity of the racket, just before it is impacted by the ball
Since the racket swings freely about point O, we can write an equation representing the conservation of angular momentum for the racket and ball about point O. In this equation, the angular momentum of the racket and ball before the impact is equal to the angular momentum of the racket and ball after impact. We have:
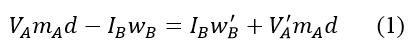
Where:
mA is the mass of the ball
IB is the moment of inertia of the racket about point O, about an axis pointing out of the page
VA' is the velocity of the ball, just after it impacts the racket. It is assumed that this velocity is parallel to VA
wB' is the angular velocity of the racket, just after it is impacted by the ball
The impact between ball and racket is inelastic and results in energy loss. This energy loss can be mathematically represented with the following coefficient of restitution equation, given by:
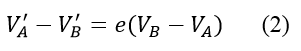
Where:
e is the coefficient of restitution
VB is the velocity of the racket at the location where it impacts the ball, just before impact
VB' is the velocity of the racket at the location where it impacts the ball, just after impact
From the kinematics of the problem we can write the following equations:
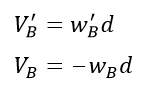
Equation (2) can therefore be rewritten as:
Lastly, combine equations (1) and (3) to solve for VA'. We have:
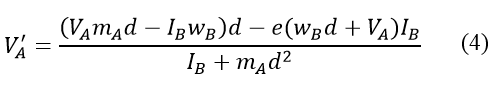
At first glance this equation doesn't seem very informative. But in fact, very useful information comes out of this equation if we observe the trend in VA' as a function of d. A plot of this trend is given in the following figure.
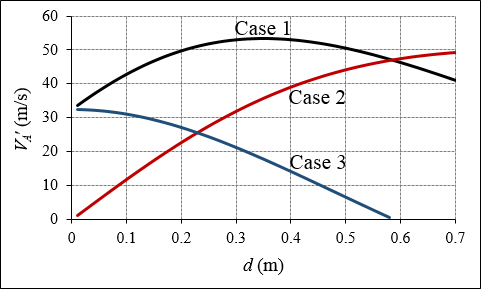
In this figure,
Case 1 represents the situation where you have a swinging racket hitting an oncoming ball. In this situation, representative values of the following are used in equation (4):
VA = 65 m/s
mA = 0.058 kg
IB = 0.04 kg·m2
wB = 80 rad/s
e = 0.5
Case 2 represents the situation where you have a swinging racket hitting a stationary ball, such as during a serve. In this situation, representative values of the following are used in equation (4):
VA = 0 m/s
mA = 0.058 kg
IB = 0.04 kg·m2
wB = 80 rad/s
e = 0.5
Case 3 represents the situation where you have an oncoming ball hitting a stationary racket. This situation does not really apply in a game of tennis but it's interesting nonetheless. In this situation, representative values of the following are used in equation (4):
VA = 65 m/s
mA = 0.058 kg
IB = 0.04 kg·m2
wB = 0 rad/s
e = 0.5
As shown in Case 1, the best spot to hit an oncoming ball to get the highest rebound velocity of the ball is somewhere in the middle of the racket.
As shown in Case 2, the best spot to serve a ball to get the highest ball velocity is near the end of the racket.
As shown in Case 3, the best spot for an oncoming ball to hit a stationary racket in order to get the highest rebound velocity of the ball, is near the handle (this clearly wouldn't work in a real game, and is not a situation that would apply anyway).
For all cases it is assumed that the length L of the racket is 0.7 m, which corresponds to the maximum value of d.
The results shown for these three cases are explained further by Rod Cross on his tennis physics page (reference: http://www.physics.usyd.edu.au/~cross/tennis.html). He is a physicist and retired academic of the University of Sydney, and has carried out a lot of analysis on the physics of tennis. The figure below shows the main spots on a tennis racket, which is based on material from his webpage.
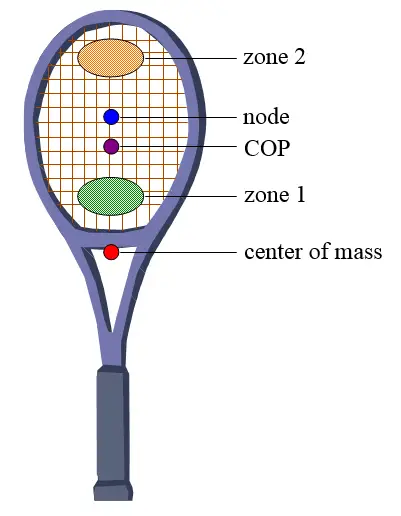
For Case 1, the best spot to hit the ball is in zone 1. For Case 2, the best spot to hit the ball is in zone 2.
The node corresponds to the point on the racket resulting in minimal racket vibration when the ball hits there. The COP corresponds to the center of percussion. At this point there is minimal reaction force exerted on the hand (at the location of the handle) when the ball hits there.
There's a ton of science involved in tennis. I've only touched on it briefly. If you want to learn more about the physics and science of tennis check out these publications by Rod Cross.
R.C. Cross, The bounce of a ball, Am. J. Phys. 67, 222-227 (1999). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/5.%20BallBounce.pdf
R.C. Cross, Ball trajectories - factors influencing the flight of the ball. http://www.physics.usyd.edu.au/~cross/TRAJECTORIES/42.%20Ball%20Trajectories.pdf
R.C. Cross, A double pendulum model of tennis strokes, Am. J. Phys. 79, 470-476 (2011). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/49.%20TennisDPend.pdf
R.C. Cross, Customising a tennis racket by adding weights, Sports Engineering, 4, 1-14 (2001). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/16.%20Customising.PDF
R.C. Cross, Impact of a ball with a bat or racket, Am. J. Phys. 67, 692-702 (1999). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/9.%20ImpactofBall.pdf
R. Bower and R.C. Cross, String tension effects on tennis ball rebound speed and accuracy during playing conditions, Journal of Sports Sciences, 23, 765-771 (2005). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/28.%20StringTEffects.PDF
R.C. Cross, Oblique impact of a tennis ball on the strings of a tennis racket, Sports Engineering, 6, 1-20 (2003). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/24.%20ObliqueImpact.PDF
R.C. Cross, Effects of friction between the ball and strings in tennis, Sports Engineering, 3, 85-97 (2000). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/10.%20StringFriction.PDF
R.C. Cross, The sweet spots of a tennis racket, Sports Engineering, 1, 63-78 (1998). http://www.physics.usyd.edu.au/~cross/sweetspots.pdf
R.C. Cross, Why bows get stiffer and racquets get softer when the strings are added, Am. J. Phys. 69, 907-910 (2001). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/17.%20Bows.PDF
Return to The Physics Of Sports page
Return to Real World Physics Problems home page