About me and why I created this physics website.

Center Of Percussion

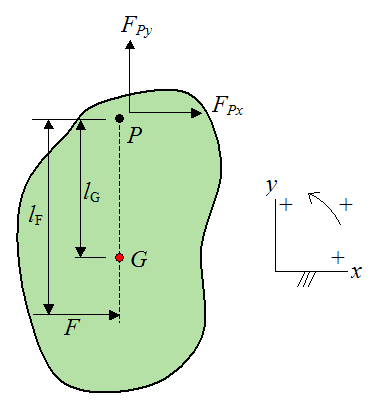
The center of percussion is a point on a pin-supported object where a perpendicular impact will produce no reaction force at the pivot point.

To set up the analysis of the problem draw a schematic of a general rigid body swinging in the plane about a fixed pivot point P, which is assumed to be frictionless.



Where:

F_Px is the x-component of the force exerted on the body by the fixed pivot P

F_Py is the y-component of the force exerted on the body by the fixed pivot P

G is the center of mass of the body

F is the perpendicular impact force exerted on the body

l_F is the distance from the point P to the contact point of F

l_G is the distance from the point P to the center of mass G


We wish to find the distance l_F so that F_Px = 0. This means that there will be no reaction force at P due to the impact force F.


Treat this as a two-dimensional problem (in the xy plane) involving rigid body dynamics. To solve this type of problem in general we need one moment equation and two force equations (in the x, y directions).

The moment equation for rotation about a fixed point P is:



Where:

ΣM_P is the sum of the moments about the fixed point P

I_P is the moment of inertia of the body about P, about an axis pointing out of the page

α is the angular acceleration of the body due to the impact force F


The sum of the moments is given by:



The angular acceleration α can be expressed as:



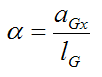
Where:

a_Gx is the linear acceleration of the center of mass of the body in the x-direction due to the impact force


From Newton's Second Law, the force equation in the x-direction is:



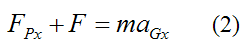
where m is the mass of the body.

For no reaction force at P, F_Px = 0

We don't need to account for the force equation in the y-direction, because the equations (1) and (2) by themselves allow us to solve the problem — since F_Px = 0 we only have to solve for two unknowns: a_Gx and l_F.

Solving, we get



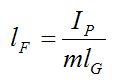
This is the general formula for calculating the distance from P to the center of percussion of the body.

This result is interesting. It says that no matter how large the impact force F is, the reaction force F_Px will always be zero.


In baseball, the centre of percussion on a baseball bat is known as the “sweet spot”. This is the location on the bat that is generally regarded as the best spot for hitting the baseball. It minimizes vibration of the bat and results in the maximum energy delivered to the ball, meaning it travels the farthest.

The "sweet spot" is a special point on the bat. When the ball strikes there, the result is minimal stinging of the hands at the grip location on the handle (the pivot). Baseball players claim that hitting the ball in this location "feels" the best, and results in the most solid hit.



Return to Dynamics page


Return to Real World Physics Problems home page