About me and why I created this physics website.
The Physics Of Ice Skating
Source: http://www.flickr.com/photos/coolmikeol/4054538571
For the most part, the physics behind ice skating comes down to analyzing the movement of skates over the ice. The skates do two things: They glide over the ice and they push off the ice with the edge, which causes a gain in speed. With practice, this combination of movements can become as effortless as walking.
Another part of the physics is the low friction of the skate blade with the ice. This low friction allows a skater to easily glide over the ice surface, and in addition, the physical properties of the ice allows a skater to dig in with his skate in order to go around a turn, speed up, or stop.
A skater propels himself forward by pushing off the ice with a force perpendicular to the skate blade. Since the friction of the blade with the ice is almost zero, this is the only way he can propel himself forward. The figure below illustrates the physics behind this principle.
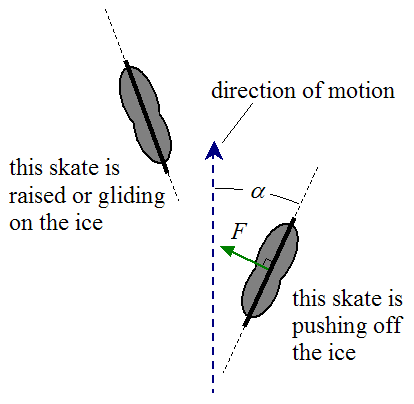
As the skater pushes off with his rear leg, a perpendicular force F is exerted on the skate by the ice. The component of the force F that points forward (in the direction of motion) is what pushes the skater forward. At the same time, his other skate is either raised or gliding on the ice. As the skater moves forward he then switches to the other leg and pushes off the ice with that one, and the process is mirrored. To push off the ice with greater forward force (and accelerate faster), the skater increases the angle α, which increases the component of force in the direction of motion.
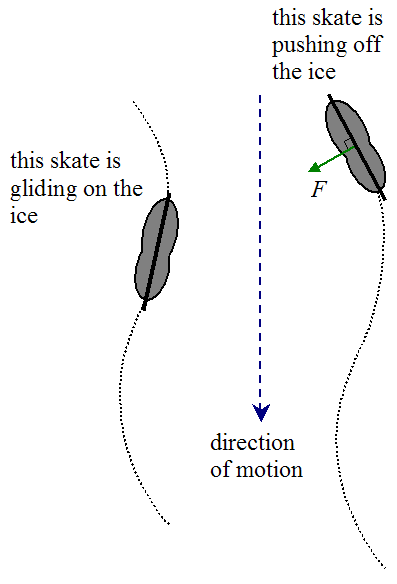
A skater can also skate backwards using a gliding pattern in the shape of a lazy "S" (as shown below), in which the skater's blades never leave the ice. However, the skater cannot push off against the ice as hard as he does when skating forward, which means he cannot go as fast. In this technique, the skater pushes against the ice with his push-skate facing inward, while his other skate glides. As the skater moves backwards he then switches to the other leg and pushes off the ice with that one, and the process is mirrored. Thus, the physics of skating backward is similar to the physics of skating forward.
A skater can at most move his feet at about 7 m/s, and the greatest forward push force will be when he begins skating from rest. At this point the velocity of his foot relative to the ice is 7 m/s. As the skater gains speed this relative velocity changes. For example, if the skater reaches a speed of 5 m/s, the relative velocity of his foot relative to the ice is 2 m/s (assuming he moves his leg backwards, with no sideways component of velocity), and the push force is less as a result. Consequently, there is a maximum speed a skater can reach, which is directly influenced by how fast he can move his feet on the ice. However, the maximum speed the skater can reach is not necessarily 7 m/s. It can be much more than this if the skater, when pushing off the ice, moves his leg backward with a sideways component of velocity. Analyzing the physics to determine the maximum speed involves looking at the biomechanics of the skater.
To maintain his balance when accelerating forward, a skater will crouch (or bend) forward in the direction of motion. This prevents him from falling (tipping) backwards due to the torque caused by the forward component of the force F. By crouching (or bending) forward, the skater is moving his center of mass forward which creates a counter-torque. This counter-torque balances the torque caused by the forward component of F, and this prevents him from falling (tipping) backwards.
Crouching (or bending) forward also reduces a skater's air resistance (drag) by reducing his frontal area. This allows him to accelerate to, and maintain, a greater speed.
In the sport of speed skating, skaters use clapskates which hinge at the front. This allows the blade to remain flattened against the ice when the skater raises his heel, during the stride. This increases the time that the skater can push off against the ice, which enables him to accelerate faster. This design trick is of a more practical nature, while still being related to the physics of ice skating.
In some ice skating sports, such as figure skating, movement on the ice involves artistry and technical skill, while in other sports, such as speed skating, movement on the ice is of a strictly technical nature and is geared towards speed and efficiency. The picture below shows a speed skater going around a track.
Source: http://en.wikipedia.org/wiki/Speed_skating. Author: http://commons.wikimedia.org/wiki/User:McSmit
When the skater is on the straight part of the track his strides are wider than on the curved part of the track. The reason for this is because on the curved part of the track it is easier to steer around the turn if he keeps the lateral distance between his strides small. However, the trade-off is that he can't go as fast around a turn as he can on the straight part of the track.
In short track speed skating the radius of the turn is quite small. This introduces considerable "lean" of the skaters towards the inside of the turn, due to centripetal acceleration. As a result, short track speed skaters can't do much skating around the turns. They must mostly ride the turns using the momentum gained on the straight part of the track. The picture below shows speed skaters as they go around a turn.
Source: http://www.flickr.com/photos/johnthescone/362893375
The centripetal acceleration of speed skaters as they go around the turns will be analyzed next.
Physics Of Ice Skating – Short Track Speed Skating Analysis
The figure below shows a schematic of a speed skater as he goes around a turn. Note that the skating surface is flat and horizontal.
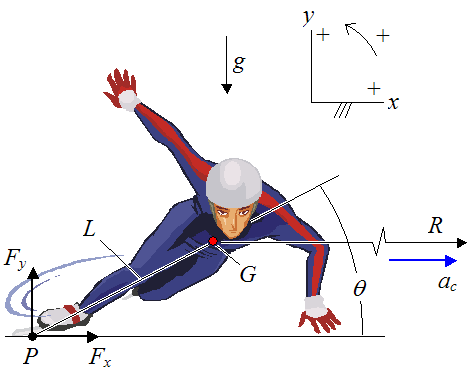
Where:
g is the acceleration due to gravity, which is equal to 9.8 m/s2 on earth
G is the center of mass of the system (which consists of skater plus skates, which together can be treated as a rigid body)
P is the approximate contact point between the skater's blades and the ice
L is the distance between point P and point G
Fx is the horizontal contact force, with the ice, acting on the skater's blade at point P
Fy is the vertical contact force, with the ice, acting on the skater's blade at point P
R is the radius of the turn, measured from the center of the turn to the center of mass G of the system
ac is the centripetal acceleration of point G. This acceleration is in the horizontal direction and points towards the center of the turn
θ is the angle between the horizontal and the line passing through points P and G. This is the angle of "lean" (a constant)
The center of mass G has zero vertical acceleration. Therefore, the forces in the vertical direction acting on the system must sum to zero. Mathematically this can be written as
where m is the mass of the system (which consists of skater plus skates).
Apply Newton's second law in the horizontal direction:
The centripetal acceleration is given by
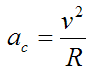
where v is the velocity of the center of mass G. This velocity is pointing out of the page.
Substitute this equation into the previous equation and we get
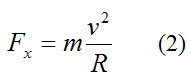
Since θ is constant, the system is in a state of rotational equilibrium. This means there is zero moment acting on the system about the center of mass G, about an axis pointing out of the page. Mathematically we can write this as
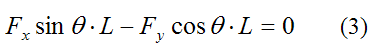
(Note that we are ignoring three-dimensional effects in this equation. They are assumed to be negligible).
Combine equations (1)-(3). We get
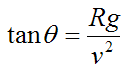
Based on this result we can do a sample calculation. For example, let's say R = 8.5 m and v = 10 m/s. The angle of lean is θ = 39.8° .
This concludes the discussion on the physics of ice skating.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page