The Physics Of Figure Skating
The Physics Of Figure Skating – Rotation

Source: http://commons.wikimedia.org/wiki/User:Dobromila
Perhaps the most common subject of analysis in figure skating physics, is rotation. Rotation occurs often in the jumps. When a figure skater makes a jump, he increases his rotation speed by pulling together his arms and legs. This reduces his rotational inertia causing him to spin faster.
The simple physics equation describing this phenomenon is given by:
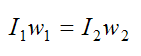
where I is the rotational inertia about the spin axis and w is the rotation rate. The subscripts 1 and 2 indicate "initial" and "final", respectively. This equation is the mathematical expression for conservation of angular momentum for a body which experiences no external torque. In the case of the figure skater, there is no outside force causing his body to rotate after he initiates his spin, so to spin faster he pulls together his arms and legs, which reduces his rotational inertia I and his rotation speed increases as a result.
The Physics Of Figure Skating – The Death Spiral
The death spiral is another interesting subject of analysis in the physics of figure skating. It is a move executed by figure skating pairs. The male skater pulls his female partner around in a circle, as shown below.

Source: http://commons.wikimedia.org/wiki/User:Kcr
The male skater must plant the front tip of his blade firmly in the ice as he pulls his partner around in a circle. This is due to the centripetal acceleration the pair experience during the rotation. The figure below shows the same figure, with labels indicating the important quantities affecting the physics of the problem.
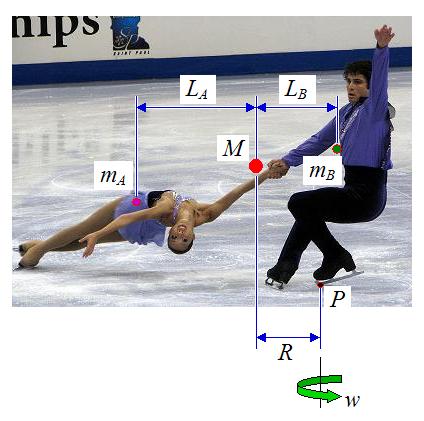
Where:
mA is the mass of the female skater
mB is the mass of the male skater
M is the mass of the system, which is equal to the combined mass of the male and female skater (M = mA + mB). Note that the red dot represents the location of the center of mass of the system.
LA is the distance from the center of mass of the female skater to the center of mass of the system M
LB is the distance from the center of mass of the male skater to the center of mass of the system M
P is the pivot point (center of rotation) of the system. This is where the front tip of the male skater's blade is planted into the ice
R is the radius of the circle traced by the center of mass of the system M, about point P
w is the rotation rate, in radians/s
Note that LB < LA. This is because the male skater weighs more than the female skater, so the center of mass is closer to him.
As the pair rotate they move as a single unit and as a result, they can be analyzed as a rigid body.
From Newton's Second Law:
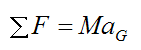
Where:
ΣF is the sum of the forces acting on the rigid body
M is the mass of the rigid body
aG is the acceleration of the center of mass G of the rigid body
Next, we can draw a simple free-body diagram in the plane of rotation, that considers only the motion of the center of mass of the figure skating pair.
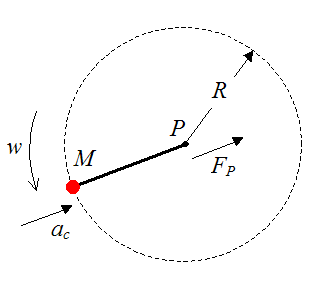
Where:
ac is the centripetal acceleration of the center of mass M due to the rotation rate w. This acceleration points towards the center of the circle (of radius R)
FP is the force exerted by the ice on the male skater's blade at point P. This force acts in the direction of the centripetal acceleration ac
It is useful to calculate FP because it tells us how much force the male skater must exert on the ice to maintain his center of rotation at point P.
The (centripetal) acceleration of M is:
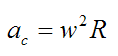
Therefore,
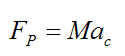
and
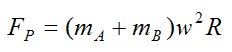
Now, let's look at some typical values so we have an idea of how much force FP the skater must exert on the ice.
mA = 50 kg (mass of female skater)
mB = 80 kg (mass of male skater)
w = 3.8 radians/s
R = 0.40 meters
Substituting, we get FP = 750 N. This is equal to about 75 kg of force that the male skater must exert on the ice. This is a bit less than his body weight, so it's a reasonable exertion. This is why he must crouch down low, since that gives him sufficient leverage to maintain his position as he rotates. And with his other skate he maintains his balance by laying the blade sideways on the ice as he goes around.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.