About me and why I created this physics website.

Parallel Axis And Parallel Plane Theorem

For three-dimensional dynamics problems, the inertia terms of a body relative to one reference frame, can be calculated based on the inertia terms relative to another reference frame with origin at the center of mass. The figure below illustrates this.





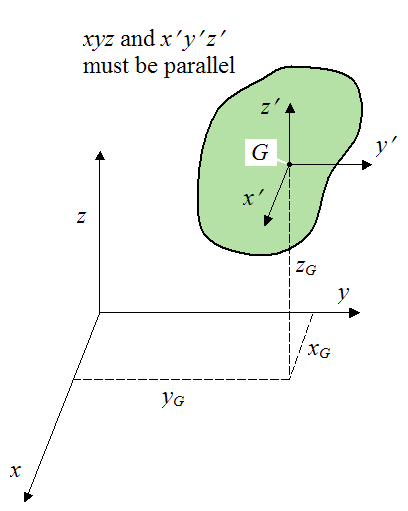
We wish to calculate the inertia terms relative to xyz given the inertia terms relative to x′y′z′ (with origin at the center of mass G of the body).


Using the parallel axis theorem for the rotational inertia terms:




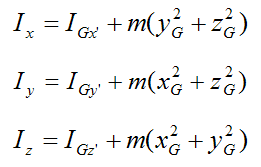
Using the parallel plane theorem for the product of inertia terms:



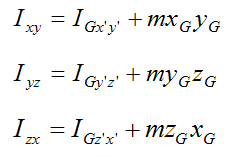
When using these equations it is necessary that the two reference frames xyz and x′y′z′ are parallel.


These formulas are useful for composite bodies of known inertia (about their center of mass), which are attached together such that the center of mass of the whole system is offset from the center of mass of the individual bodies. For example, let’s say we have a sphere attached to a slender rod, and the center of mass of this system (consisting of sphere and slender rod) is offset from the center of mass of either the sphere or rod. Using the parallel axis and parallel plane theorem you can add the inertia terms for the sphere and rod together to obtain the inertia terms for the whole system.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page