About me and why I created this physics website.

Torque

Torque is defined as the tendency to rotate an object when it is subjected to a force. It is a function of the magnitude of the force, the direction of the force, and the "arm". See figure below.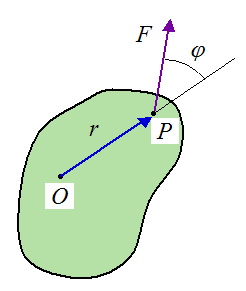





Define the following variables:

τ is the torque (a vector)

r is the arm (a vector) from the point of rotation O to the contact point P (where the force acts)

F is the force (a vector)

φ is the angle between r and F, as shown

u is a unit vector acting in the direction of the tοrque τ


Tοrque can be expressed mathematically, as follows



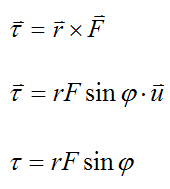
In the last two equations, τ, r, and F do not have the vector "hat" because here they represent the magnitude of vectors τ, r, and F (respectively).


The rotation point O (and therefore r) can be chosen arbitrarily when solving a dynamics problem, since this choice will not affect the solution. However, it may be easier and mathematically more convenient to choose a point which "intuitively" makes sense, such as the hinges of a door. Also, O does not need to be a fixed point. It can be a moving point on a body (e.g. the center of mass). This becomes clearer when solving actual dynamics problems, which many times involve calculating tοrque about the center of mass.

The direction of τ can be visualized using the right-hand rule. If one imagines which direction the object will tend to rotate when acted upon by the force F, and then curling the fingers of your right hand in that direction, your thumb will give the direction of the τ vector. For the figure above, the τ vector is pointing out of the page.

Note that tοrque is sometimes called the "moment" of a force, which specifically means the "moment arm rsinφ" of the force F. The moment arm rsinφ is the component of r that is perpendicular to F. This is simply a different naming convention.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page