About me and why I created this physics website.
Coriolis Force
To explain the Coriolis force it is first necessary to explain Coriolis acceleration.When an object simultaneously rotates about a point and moves relative to that point, an acceleration results from this. This acceleration is called Coriolis acceleration.
To illustrate this acceleration, consider a particle P rotating in a plane about point O with a constant angular velocity w, and moving radially outwards with a velocity vr. The Coriolis acceleration is denoted by ac. It acts in the circumferential direction (perpendicular to vr).
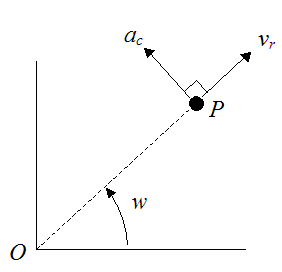
From the equations from Curvilinear motion:
By applying Newton’s Second Law in the direction of ac, we can determine the force acting on the particle P due to this acceleration. Call this force Fc.
where m is the mass of the particle.
To gain an intuitive understanding of the acceleration ac, think about what happens as the particle P moves radially outwards. It traces a circle of progressively larger radius. Given that the angular velocity w is constant, and the velocity of the particle tangent to the circle is equal to wR (where R is the radius of the circle), the tangential (circumferential) velocity must then increase as a result. The figure below shows the tangential velocity vT of the particle P at two consecutive instants.
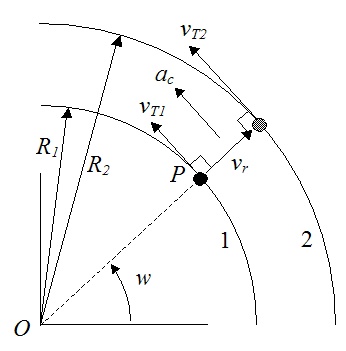
Since R2 > R1,
Therefore there is an acceleration ac (in the direction shown) due to this tangential increase in velocity.
Thus, the particle P must have a restraining force Fc acting on it in the direction of ac, in order to maintain its radially outward motion.
Note that this restraining force Fc is not necessarily the total force acting on the particle P. It is only the part of the force that is due to the combined effect of the particle simultaneously rotating about point O and moving radially outwards from point O.
Now, let’s define a reference frame that has origin at point O and is rotating at angular velocity w. If the restraining force Fc were to vanish (or at least decrease), the particle P would travel a curved path relative to this (rotating) reference frame (as will be explained). The apparent force causing the particle to curve is called the Coriolis force. Note however, that the Coriolis force is a fictitious force, and not a real force, since it is based on motion relative to a non-inertial reference frame, that is rotating. Nevertheless, it can be an informative way of looking at a problem, as will be shown.
For example, let’s say we have a merry-go-round rotating with a constant angular velocity. On the merry-go-round there is a ball rolling outwards from the center with a radial velocity vr (this is the velocity of the ball relative to the merry-go-round). This results in the ball moving in a straight line relative to the merry-go-round (in the direction of vr). The force that maintains this straight-line motion is the restraining force Fc (calculated before).
Now, let’s say there is no restraining force (Fc = 0). This would result in the ball not being able to increase its tangential speed (since ac = 0 by equation (1)). Consequently, the ball must “fall back”, which will result in the ball moving along a curved path relative to the merry-go-round. Thus, from the point of view of an observer sitting on the merry-go-round, the ball would appear to be “pushed” by an imaginary force (called the Coriolis force) causing it to curve.
The figure below shows the motion of the ball relative to the merry-go-round, as the merry-go-round rotates between positions 1 and 2. The figure illustrates two cases: The first case is where the restraining force Fc is present – this is illustrated with the straight (green) line. The second case is where Fc = 0 – this is illustrated with the blue curve.
The black arrow shows the motion of the ball relative to an inertial reference frame (ground) for the case where there are no external forces acting on the ball in the plane of the merry-go-round.
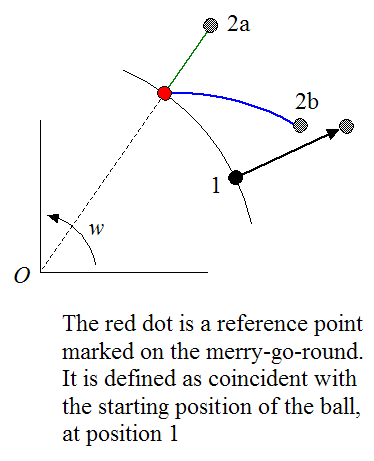
In the above figure:
The starting position of the ball is denoted by ‘1’
In the presence of a restraining force Fc , the final position of the ball is denoted by ‘2a’
If the restraining force Fc = 0 , the final position of the ball is denoted by ‘2b’
As mentioned already, the green line represents the motion of the ball relative to the merry-go-round for the case where Fc is present. The blue curve represents the motion of the ball relative to the merry-go-round for the case where Fc = 0 (but note that even if Fc = 0, there may still be other forces acting on the ball in the plane of the merry-go-round).
For the situation where Fc is not equal to zero but is less than the restraining force in the first case, the path traveled by the ball (relative to the merry-go-round) would follow a curved path that lies somewhere in between the green line and the blue curve.
From the point of view of an observer sitting on the merry-go-round (and moving with it), the Coriolis force is the apparent force that appears to be acting on the ball, causing it to veer to the right.
More specifically, the Coriolis force acts in a direction that is perpendicular to both the angular velocity vector and the relative (linear) velocity vector.
Referring to the figure above this would mean that the (fictitious) Coriolis force acts perpendicular to the blue curve (where Fc = 0), since the angular velocity vector of the merry-go-round is pointing out of the page, and the relative (linear) velocity vector of the ball relative to the merry-go-round is tangent to the blue curve.
The Coriolis force acting on the ball is indicated by the black arrows, shown below.
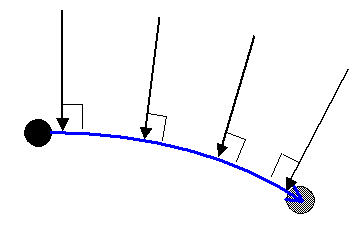
The Coriolis force explains why the ball tends to curve in on itself, relative to an observer sitting on the merry-go-round (and moving with it).
The black arrow shown in the previous figure (with starting position '1') represents the path traveled by the ball relative to ground (an inertial reference frame), for the situation where no external forces are acting on the ball in the plane of the merry-go-round (i.e. there is no friction with the merry-go-round surface). In this situation, the ball would travel a straight line (relative to ground) indicated by the black arrow (due to Newton’s First Law). However, relative to the merry-go-round, the ball would follow a curved path, similar to the blue curve.
Centrifugal Force And Euler Force
The Coriolis force is not the only fictitious force that acts on the ball from the point of view of an observer sitting on the rotating merry-go-round. There is also a Centrifugal force, which appears to be pushing the ball radially outwards from the center of rotation O. This force is explained in more detail here.
Now, if the merry-go-round has an angular acceleration, this would introduce yet another component of motion for the ball (relative to the merry-go-round). This component of motion points in the circumferential direction of the merry-go-round and has the effect of contributing to the deflection of the ball in the circumferential direction of the merry-go-round. This would add yet another fictitious force called the Euler force. From the point of view of an observer sitting on the merry-go-round, the Euler force appears to be pushing on the ball in the circumferential direction. This force is explained in more detail here.
Therefore, there are three fictitious forces acting on the ball for the general case where the merry-go-round is rotating with a given angular velocity, and with a given angular acceleration. These fictitious forces are illustrated in the figure below.
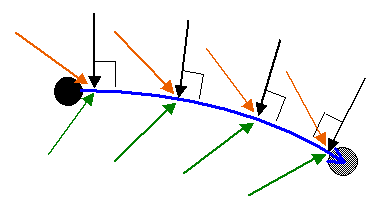
The black arrows represent the Coriolis force, which acts perpendicular to the path of the ball represented by the blue curve.
The green arrows represent the Centrifugal force, whose line of action passes through the center of rotation O.
The orange arrows represent the Euler force, which acts in the circumferential direction, and is perpendicular to the Centrifugal force.
These three fictitious forces all combine to produce the relative motion of the ball relative to the merry-go-round.
Understanding fictitious forces can be useful for understanding everyday phenomenon. For example, the rotation of cyclones on Earth is influenced by the Coriolis force, which results from the combination of Earth’s rotation and the direction of wind flow.
Return to Dynamics page
Return to Real World Physics Problems home page