About me and why I created this physics website.
Bouncing Ball Physics
Bouncing ball physics is an interesting subject of analysis, demonstrating several interesting dynamics principles related to acceleration, momentum, and energy. These principles will be discussed.
Almost everybody, at some point in their lives, has bounced a rubber ball against the wall or floor and observed its motion. Normally we don't think about the physics of bouncing balls too much as it's fairly obvious what is happening – the ball basically rebounds off a surface at a speed proportional to how fast it is thrown. But what isn't known to most is what is specifically happening to the ball before, during, and after its brief impact with the surface.
To begin this explanation let's first consider what happens to a typical rubber ball that is dropped vertically onto a flat horizontal surface, and which falls under the influence of gravity.
In this explanation, the bouncing ball physics will be broken down into seven distinct stages, in which the ball motion (before, during, and after impact) is analyzed. To simplify the discussion let's assume that the bounce surface is hard (rigid), and that air resistance is negligible.
Let's define the geometric center of the ball as point C, the velocity of point C as V, and the acceleration of point C as a. Let's further assume that the ball has uniform density, which means that point C of the ball coincides with its center of mass.
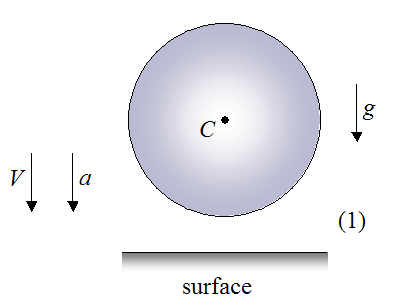
Stage 1
In this stage, the ball falls vertically downward under the influence of gravity (g). The velocity V points downward. The acceleration a also points downward. The magnitude of a is equal to g, in the absence of air resistance. (Note that the acceleration due to gravity is g = 9.8 m/s2, on earth).
Stage 2
In this stage, the ball begins to make contact with the surface. It continues to fall vertically downward under the influence of gravity. The velocity V and acceleration a (equal to g) both continue to point downward.
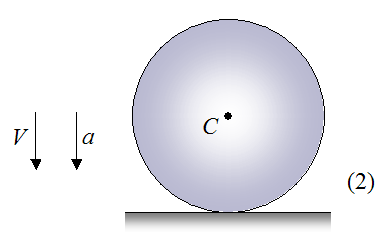
Stage 3
In this stage, the ball has slowed down. The velocity V is still pointing downward. However, the ball has deformed sufficiently such that the acceleration a is now pointing upward. This means that the ball has deformed enough such that it's pushing against the surface with a force greater than its own weight. As a result, the acceleration a is pointing upward.
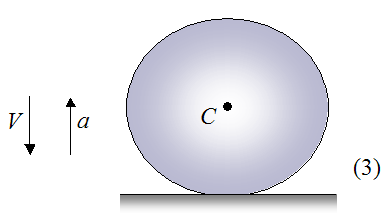
Stage 4
In this stage, the ball has reached its maximum deformation. As a result, the acceleration a is still pointing upward, and the velocity V is zero. This means that point C is at its lowest point.
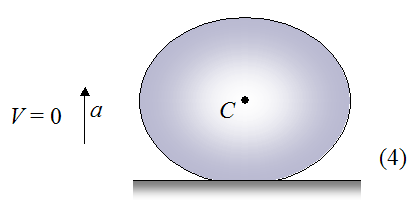
Stage 5
In this stage, the ball velocity V is increasing and pointing upward since the ball is now in the rebounding stage. As a result, the ball is less deformed than in the previous stage, but is still deformed enough such that it's pushing against the surface with a force greater than its own weight. This means that the acceleration a is still pointing upward.
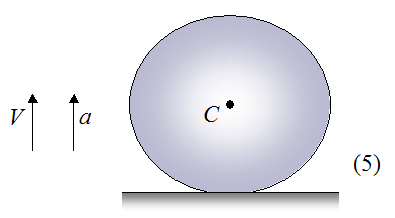
Stage 6
In this stage, the ball is barely touching the surface. The velocity V is still pointing upward since the ball is still in the rebounding stage. However, since the ball is no longer deformed it has essentially zero contact force with the surface. This means that the only force acting on the ball is gravity. As a result, the acceleration a is now pointing downward, and the upward velocity V is now decreasing.
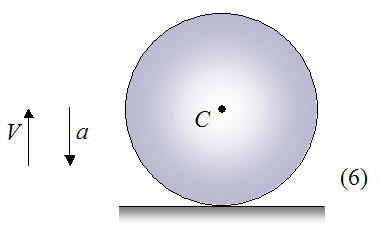
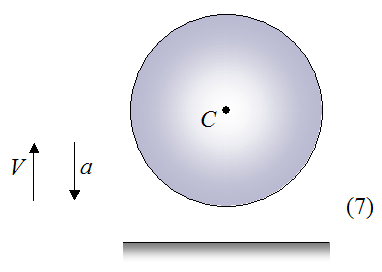
Stage 7
In this stage, the ball has fully rebounded and has lifted off from the surface. The velocity V is still pointing upward, and the acceleration a is still pointing downward since the only force acting on the ball in this stage is gravity.
Special Case Of Bouncing Ball Physics
The physics of a bouncing ball can become particularly interesting for certain cases. For example, certain types of balls (such as SuperBalls) can be given a backspin and (after the bounce) the velocity and rotation of the ball will reverse direction. The figure below illustrates this.
For simplicity, assume the ball motion is planar (two-dimensional).
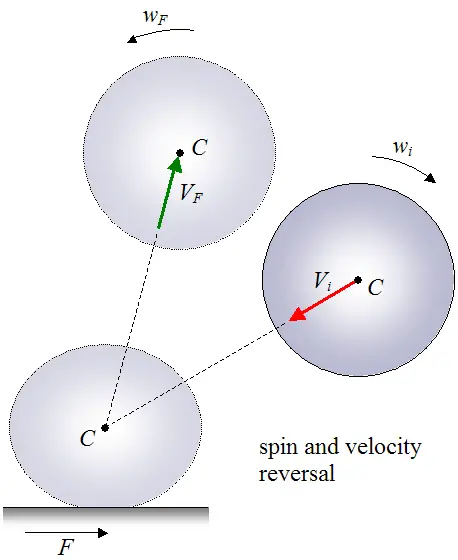
As shown in the above figure, the horizontal force F is the friction force acting on the ball due to contact with the surface, during impact. This force F is the cause of the velocity and spin (rotation) reversal. This friction force is generated by the gripping action of the ball with the surface. The direction of this friction force is opposite the direction of slip velocity between ball and surface, during impact. Slip velocity is the relative horizontal speed between the ball’s point of impact and the surface it is impacting.
Since this force F is acting to the right, it torques the ball counterclockwise. This causes the ball to change its original spin direction from clockwise wi to counterclockwise wF, after impact. This force also causes the ball to accelerate to the right during impact. This results in the horizontal velocity component of the ball (parallel to the surface) to change direction and point towards the right, after impact.
In order for the ball velocity and spin to reverse direction it is necessary to have a high coefficient of friction between ball and surface. This creates sufficient friction force F to be generated, which causes the spin and horizontal velocity component of the ball to reverse direction after impact with the surface.
In classical mechanics books, bouncing ball physics problems are often modeled as being elastic. In other words, it is assumed that the kinetic energy of the ball is conserved before and after the bounce. In reality, this is not the case. At best, a ball can only be nearly elastic, such as a SuperBall.
The picture below clearly shows a bouncing ball captured with a stroboscopic flash (at 25 images per second). You can see the ball gradually lose height, due to the loss of kinetic energy after each bounce.
Source: http://en.wikipedia.org/wiki/Coefficient_of_restitution. Author: http://commons.wikimedia.org/wiki/User:Richard_Bartz
To properly account for the inelastic nature of real world bouncing ball physics problems, it is common to introduce a coefficient of restitution, which accounts for the loss of kinetic energy during each bounce. This coefficient, coupled with impulse and momentum equations, allows one to solve for the linear and/or angular velocities of the ball before and/or after the bounce.
I put together some very useful references which explain in great detail bouncing ball physics. These references are taken from Rod Cross's publications page. He is a physicist and retired academic of the University of Sydney. He has done extensive study on bouncing ball physics, largely in the area of sports.
R.C. Cross, The coefficient of restitution for collisions of happy balls, unhappy balls and tennis balls, Am. J. Phys. 68, 1025-1031 (2000). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/12.%20Unhappy.PDF
R.C. Cross, The bounce of a ball, Am. J. Phys. 67, 222-227 (1999). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/BallBounce.pdf
R.C. Cross, Impact of a ball with a bat or racket, Am. J. Phys. 67, 692-702 August (1999). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/9.%20ImpactofBall.pdf
R.C. Cross, Grip-slip behaviour of a bouncing ball, Am. J. Phys. 70, 1093-1102 (2002). http://www.physics.usyd.edu.au/~cross/Gripslip.pdf
R.C. Cross, Bounce of a spinning ball near normal incidence, Am. J. Phys. 73, 914-920 (2005). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/31.%20Spin.pdf
R.C. Cross and A. Nathan, Experimental study of the gear effect in ball collisions, Am. J. Phys. 75, 658-664 (2007). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/37.%20GearEffect.pdf
R.C. Cross, Impact of a ball on a surface with tangential compliance, Am. J. Phys. 78, 716-720 (2010). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/47.%20MoreSpin.pdf
R.C. Cross, Rolling motion of a ball spinning about a near-vertical axis, The Physics Teacher, 50, 25-27 (2012). http://www.physics.usyd.edu.au/~cross/PUBLICATIONS/55.%20RollingBall.pdf
I created a handwritten solution in which I analyze a ball bouncing off a moving surface. In this solution I work out the equations which determine the rotational and linear velocity of the ball after impact. I generalised the solution to 3D (three dimensions), which can easily be reduced to two dimensions if one desires. The solution is in PDF format. You can download it by right-clicking on this link. This solution can be useful to someone who wants to create, say, a ball bounce game, and needs equations to predict how a ball moves after each bounce.
Return to Miscellaneous Physics page
Return to Real World Physics Problems home page