About me and why I created this physics website.

Conservation Of Momentum

Conservation of momentum applies to two distinct classes of motion: translational motion and rotational motion. Both must be treated independently since momentum for translational motion can be conserved while momentum for angular motion may not be conserved, or vice-versa.

Translational momentum is commonly called linear momentum and is based on the linear motion of a system of particles, such as those particles that make up a rigid or deforming body. There is no restriction on the way the particles are connected when we speak of linear momentum.

Rotational momentum is commonly called angular momentum and is based on the rotation of a system of particles about a given point. It is common to associate angular momentum with bodies that may either be rigid or deforming. However, the discussion here will focus on the angular momentum of rigid bodies.

Conservation of momentum, for linear and angular (rotational) motion, will be discussed here in detail.


Conservation Of Momentum – Linear Momentum




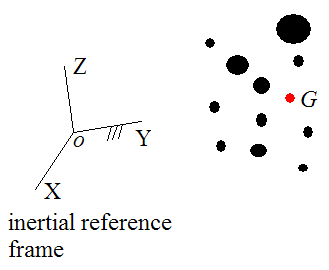
The translational motion of a system of particles that experiences no external linear impulse can be analyzed using conservation of linear momentum (which is, conservation of momentum applied to linear motion).

From the page on linear momentum we derived the following vector equation for a system of particles:



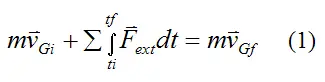
Where:

m is the total mass of the system of particles

v_Gi is the initial velocity of the center of mass G of the system of particles (at time t_i), with respect to an inertial reference frame (ground)

v_Gf is the final velocity of the center of mass G of the system of particles (at time t_f), with respect to an inertial reference frame (ground)

The term



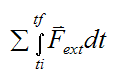
is defined as the external linear impulse acting on the system of particles (between time t_i and t_f), due to the external forces acting on the particles.

Linear momentum is conserved if no external forces act on the system of particles. This means that:



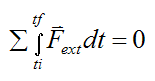
Equation (1) therefore becomes



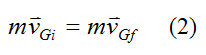
Mass cancels out and



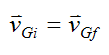
This is a nice result for conservation of momentum for the linear case. This result tells us that the velocity of the center of mass does not change if no external forces act on the system of particles. This is true even if there is collision between the particles. Collisions result in internal forces that occur in equal and opposite pairs (Newton’s Third Law). Hence, when summing over all the particles, the internal forces cancel each other out.

Equation (2) can be written as:



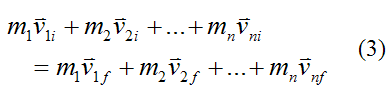
Where:

m₁, m₂,..., m_n is the mass of the individual particles in the system

v_1i, v_2i,..., v_ni is the initial velocity of the individual particles in the system, with respect to an inertial reference frame

v_1f, v_2f,..., v_nf is the final velocity of the individual particles in the system, with respect to an inertial reference frame


Equation (3) is perhaps the most useful mathematical expression for the conservation of momentum (for the linear case) of a system of particles. It can be used to solve problems involving elastic collisions or inelastic collisions between bodies, which can be treated as particles, and which are subject to no external forces (such as friction on a surface). To see an example of a solved problem that makes use of conservation of momentum for the linear case, go to The Physics Of Billiards.


Conservation Of Momentum – Angular Momentum

The rotational motion of a body that experiences no external angular impulse can be analyzed using conservation of angular momentum (which is, conservation of momentum applied to angular motion). The analysis that follows will be for a rigid body.

From the page on angular momentum we derived the following scalar equation for a rigid body experiencing planar (two-dimensional) motion:



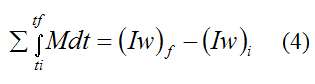
Where:

I is the moment of inertia of the rigid body, about the center of mass G of the body, or about a point O on the body that is fixed to ground

w_i is the initial angular velocity of the rigid body, with respect to an inertial reference frame (ground)

w_f is the final angular velocity of the rigid body, with respect to an inertial reference frame (ground)

The term



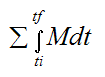
is defined as the external angular impulse acting on the rigid body (between time t_i and t_f), due to the sum of the external moments acting on the body (taken either about point G or a fixed point O on the rigid body).

Angular momentum is conserved if no external moments act on the rigid body. This means that:



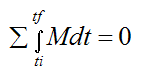
taken about either point G or a fixed point O on the rigid body.

Equation (4) therefore becomes



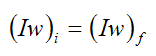
As a result, angular momentum is conserved for the rigid body (between t_i and t_f). Note that the above equation also applies for the case where the moment of inertia I is not constant, such as when the body is deforming (i.e. not rigid). For example, in the case of figure skating, when a skater performing a turn pulls in his arms his moment of inertia I decreases. In order for the above equation to hold this means that his spin rate w must increase (i.e. he spins faster). This assumes of course that there is no external moment acting on him. Figure skating spins is a common real-world example of conservation of momentum applied to angular (rotational) motion.



Let's now extend conservation of momentum for the angular case to three-dimensional motion. From the page on angular momentum we derived the following vector equation for a rigid body experiencing general three-dimensional motion:



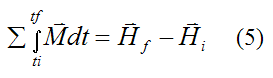
Where:

H_i is the initial angular momentum of the rigid body, about the center of mass G of the body, or about a point O on the body that is fixed to ground

H_f is the final angular momentum of the rigid body, about the center of mass G of the body, or about a point O on the body that is fixed to ground

The term



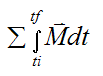
is defined as the external angular impulse acting on the rigid body (between time t_i and t_f), due to the sum of the external moments acting on the rigid body (taken either about point G or a fixed point O on the rigid body).

Angular momentum is conserved if no external moments act on the rigid body. This means that:



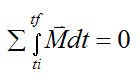
taken about either point G or a fixed point O on the rigid body.

Equation (5) therefore becomes



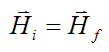
As a result, angular momentum is conserved for the rigid body (between t_i and t_f). Physically speaking, this means that the angular momentum vector H has constant magnitude and direction with respect to an inertial reference frame (ground).

To analyze the motion of a system (or body) when there is no external impulse acting on the system (or body), one can apply the equations of motion, such as those given in the rigid body dynamics page. So for the case of angular motion with no external moments, you just set the moments equal to zero in the equations of motion, and the solution will correspond to the case where angular momentum is conserved.

If you want to see an interesting paper explaining the conservation of angular momentum for semi-rigid bodies experiencing three-dimensional motion, have a look at:

Do springboard divers violate angular momentum conservation?, Cliff Frohlich, American Association of Physics Teachers, 1979.


See also, Cat righting reflex and physics of gymnastics.



Return to Dynamics page


Return to Real World Physics Problems home page