About me and why I created this physics website.

The Physics Of Gymnastics

Source: https://commons.wikimedia.org/wiki/File:Anton_Fokin_rings.JPG. Author: https://commons.wikimedia.org/wiki/User:TwoWings


Gymnastics is a sport requiring a lot of balance, strength, and technique. In the Olympics it is one of the most popular sports and certainly one of the most interesting to watch. Athletes performing at gymnastics competitions push the very limits of what their bodies can do. They also push the limits of physics. In this page I talk about the physics in some of the gymnastics events.

The Still Rings

In this event the gymnast requires a lot of upper body strength, which is fairly evident. But in addition to strength, did you know that the gymnast must also have a very fine sense of balance to keep his center of mass in just the right position, with little room for error. This is necessary in order to maintain a stationary position in the strength holds, especially when his body is in a horizontal position.

Before I get into the physics let's look at a video of a gymnast performing on the still rings.



As you can see, the gymnast performs several static moves in which he keeps his body position stationary while keeping his body lifted in either a horizontal or vertical position. You might be wondering, in addition to the strength requirement, what's involved in the physics sense?

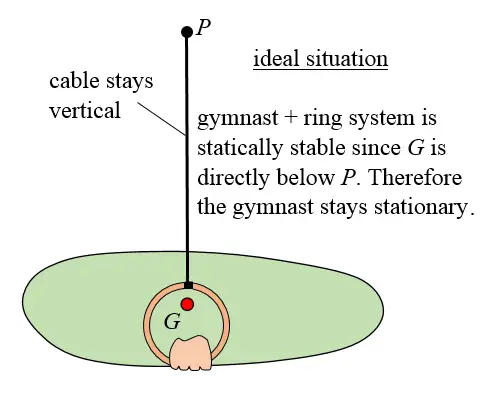
First, think of his body as a pendulum. For the gymnast to remain stationary the center of mass of his body plus rings must lie directly underneath the pivot point of the cables to which the rings are attached. If his center of mass is not directly underneath this point he will swing. It's like moving a pendulum sideways and then letting it go. It will swing. For the pendulum mass to not swing the mass must must lie directly underneath the pivot point of the pendulum. The figures below illustrate what happens when the center of mass of the gymnast plus rings does not lie directly below the pivot point of the cables. The assumption here is that the gymnast and rings together form a rigid body.



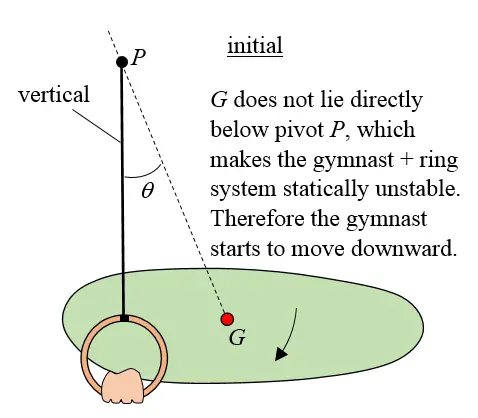
It does not matter how strong the gymnast is and how rigid he can keep his body when gripping the rings. If the center of mass of his body plus rings (G) does not lie directly underneath the pivot P he will swing. And he will swing until the center of mass lies below the pivot P, as shown in the figure below. At this point the angle θ is zero.



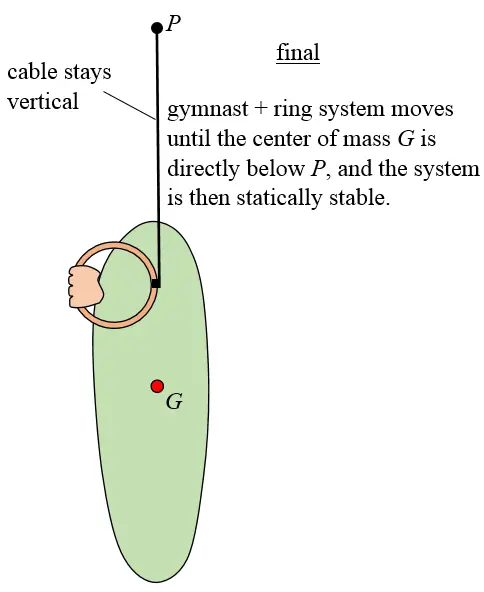
For the gymnast to maintain stationary during the static strength holds he must place the center of mass G directly below P as shown below.




The Trampoline

An interesting physics concept illustrated in the trampoline event is conservation of angular momentum. While the gymnast is in the air the only force acting on her body is gravity (assuming air resistance is negligible). The force of gravity exerts no torque about her center of mass. Therefore the angular momentum of the gymnast is conserved about her center of mass. This allows for an interesting analysis regarding her rotation while in the air.

Let's first check out a video of gymnasts performing on the trampoline.



You'll notice that on some of the mid-air rotations there is a combination of somersault rotation and twisting along the (lengthwise) body-axis. This can be analyzed as a problem in angular momentum conservation. To set up this analysis first consider the figure below showing an example somersault plus twist combination [1].



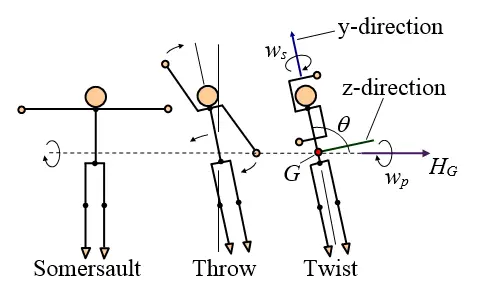
This figure is based on reference [1] by Cliff Frohlich, which illustrates how a gymnast on a trampoline can create twist along her (lengthwise) body-axis after starting off with a simple forward somersault rotation (shown on the left).

The gymnast starts with a forward somersault rotation, shown in the left diagram. The gymnast then moves her arms using a "throw" technique in the clockwise direction in the plane of her body, as shown in the middle diagram. Due to conservation of angular momentum, her body rotates in the counterclockwise direction, in the plane of her body. After the "throw" is completed and her arms are in the final position as shown in the diagram on the right, a rotation angle θ results in the plane of her body, as shown. In this new orientation at angle θ the body of the gymnast twists along the body-axis in the y-direction with angular velocity w_s along this axis. Again, this happens because of conservation of angular momentum. At the same time, the gymnast rotates along the original somersault axis (denoted by the dotted line) with a precession rate w_p. At all times the angular momentum vector H_G remains constant.

Once the arm throw is completed and the orientation of the gymnast's body reaches angle θ, this angle remains fixed throughout the gymnast's rotation. At this point the body of the gymnast can be treated as a rigid body, and an analysis can be done similar to the analysis for torque-free motion given in the gyroscope physics page.

The equations for angular velocity are given by,



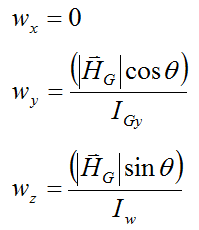
where:

w_x is the angular velocity of the gymnast, with respect to ground, resolved along the x-axis, which points out of the page (not shown). At the instant shown, this is equal to zero.

w_y is the angular velocity of the gymnast, with respect to ground, resolved along the y-axis

w_z is the angular velocity of the gymnast, with respect to ground, resolved along the z-axis

I_Gy is the principal moment of inertia of the gymnast about the y-axis, passing through the center of mass G of the gymnast

I_w is the principal moment of inertia of the gymnast about the z-axis, passing through G. Note that, due to symmetry, this is roughly equal to the principal moment of inertia of the gymnast about the x-axis. The above equation is based on the assumption that these two principal moments of inertia are equal, which is a reasonable approximation.

|H_G| is the magnitude of the angular momentum vector H_G

Note: It is assumed that the principal moments of inertia of the gymnast lie along the x, y, and z axis shown in the figure. This is based on the fact that the gymnast's body can be approximately treated as a long cylinder.

Also note that it is not clear from watching the video if the gymnasts are using a "throw" technique with their arms in order to twist along their body-axis. The video would have to be in slow motion to make this determination. However, regardless of the technique used it is conservation of angular momentum which causes the twisting, which results from some specific arm movement.

Lastly, we have the following equations, again, taken from the gyroscope physics page:



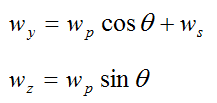
The final equation governing the number of twists per somersault is given by w_y/w_p = I_wcosθ/I_Gy. This equation comes from combining the above equations. This equation tells us that skinnier gymnasts can twist faster, since skinnier gymnasts have a larger ratio I_w/I_Gy.

Note that, at all times the gymnast rotates about her center of mass G. The movement of her center of mass is determined by Newton's second law, F = ma. In this case the only force F acting on her body is gravity. This means that the movement of her center of mass is determined only by the force of gravity and is completely independent of her rotation. Therefore, the gymnast rotates about this point, just like the only point on a wheel that moves independently of the rotation of the wheel is the wheel center, which is the point that the wheel rotates about.


Another interesting analysis involving angular momentum is the change in body orientation of a gymnast on a trampoline, in mid-air, when her angular momentum is zero. By using a coordinated sequence of movements she can change her body orientation so that she ends up facing a completely new direction. The figure below illustrates an example of this [1].



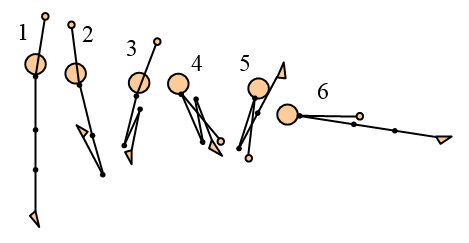
In this figure the gymnast moves from a vertical position to a roughly horizontal position using only arm and leg movements as shown. This is all due to the conservation of angular momentum, made possible by swinging the arms and legs in the sequence shown.

The figure below shows a second case where a gymnast on a trampoline, with zero angular momentum, can change her orientation in mid-air [1].



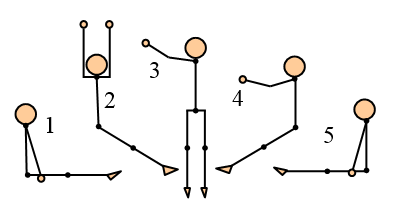
Cliff Frohlich [1] writes the following description for what happens here:

"The gymnast bounces from a sitting position (1) and begins to raise her arms over her head by bringing them forward and up. In (2), she rotates her upper body to turn her arms and shoulders as far around as possible, and she begins to drop her legs. Because her legs are piked and her arms are raised, the moment of inertia of her lower body is large relative to the amount of inertia of her upper body, and thus her legs experience little rotation. In (3) she brings her arms forward and down and "swivels" her hips beneath her while her arms are extended. In this step the moment of inertia of her lower body is smaller than that of her upper body. In (4) she brings her feet and legs up into a pike, and in (5) the stunt ends as it began, in a sitting position".


This concludes the physics of gymnastics coverage. There is a lot more that can be covered, but the analyses given here should give you an idea of what kind of physics plays a role in the sport of gymnastics.

Reference

1. C. Frohlich. Do springboard divers violate angular momentum conservation? Am. J. Phys. 47(7), July 1979.



Return to The Physics Of Sports page


Return to Real World Physics Problems home page