About me and why I created this physics website.

Work And Energy

Work And Energy – For Particles

The figure below shows a constant force F acting on a particle, which travels a distance d in the same direction as the force. The work done on the particle is given as W.





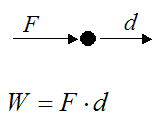
In the figure below we have F acting at an angle θ to d. The work done is evaluated by taking the component of F acting in the same direction as d.





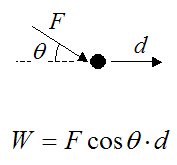
The figure below shows a more general case where the force is not constant and changes with time. Here it is necessary to evaluate an integral between the initial position of the particle (X1) and the final position (X2).





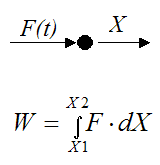
We can calculate the instantaneous power P if we know the instantaneous force F and velocity v of the particle.





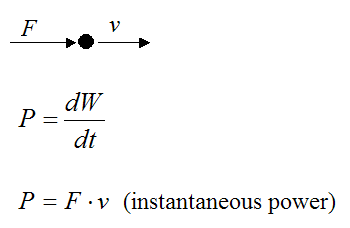
A particle of mass m moving at a velocity v has an associated kinetic energy (KE), as given below.





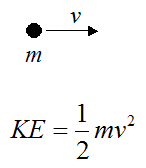
In the case where energy is conserved and there is no friction, W = KE.


Let's look at the special case where we have a mass and spring, as shown below. Here we define k as the spring constant (Hooke's Law), and x as the displacement from the equilibrium position, where the spring force F is zero.





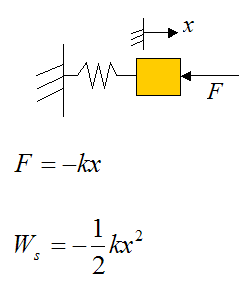
W_s is the work required to stretch or compress the spring.

The negative sign in the above two equations means that the force exerted by the spring (as it is stretched or compressed) is in the direction opposite to the spring displacement x.


In the above two equations it is assumed that the orange block is moving slow enough so that acceleration can be neglected. Thus, the force F acting on the block is equal and opposite to the force the spring exerts on the block (since by Newton's Second Law ΣF = ma = 0, where ΣF means the sum of the forces).

But whether or not the block is accelerating, the spring always exerts a force in the opposite direction of the spring displacement. This means that a spring always wants to return to its original position.


Work And Energy – For Rigid Bodies

Let's now consider a rigid body rotating about a fixed point (axis) at O.





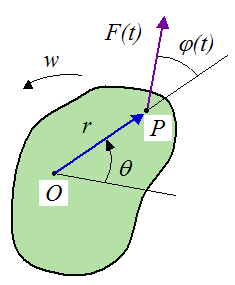
Where:

F(t) is the instantaneous force acting at point P, at time t

r is the moment arm from point O to point P

φ is the angle between r and F(t), at time t

θ is the rotation angle

w is the instantaneous angular velocity


To calculate the work done we must evaluate the following integral between an initial rotation angle θ1 and a final rotation angle θ2.





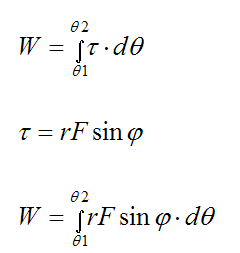
The instantaneous power is given by





The instantaneous kinetic energy of rotation is given as




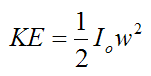
where I_o is the rotational inertia of the body about the rotation axis at point O.


In the case where energy is conserved and there is no friction, W = KE.


Summary

The main advantage of using Work and Energy methods is that it allows you to easily find the velocity of a body or system of bodies knowing how much "work" went into the system (provided energy is conserved, and there are no frictional losses). It avoids much of the effort in drawing free body diagrams and determining the direction of forces, etc.

For example, if a roller coaster rolls down a track and falls a vertical distance h, we can estimate its speed by assuming no friction on the track. We simply calculate the work done by gravity, which is mgh, where m is the mass of the roller coaster and g is the acceleration due to gravity (9.8 m/s²). The kinetic energy of the roller coaster is given by KE = (1/2)mv², where v is the speed. If we equate the work done by gravity to the kinetic energy, we can solve for v, which is v = (2gh)^1/2 (mass cancels out). This is a nice result because we do not have to know the path the roller coaster takes as it descends. We only need to know the vertical height h that it falls.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page