About me and why I created this physics website.

Rotational Inertia

A rigid body is shown below. We wish to calculate the rotational inertia (often called the moment of inertia) of the body I_G about an axis (pointing out of the page) which passes through point G (the center of mass). A particle of mass m_i is shown on the rigid body, with position (x_i , y_i).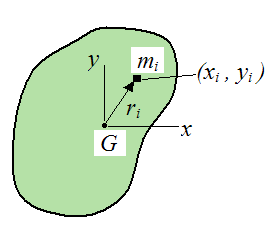





The moment of inertia of the body is the sum of the individual moments of inertia of all the particles m_i within the body. This can be expressed as




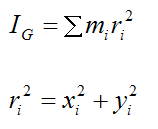
This sum can be expressed as an integral:




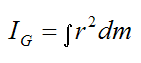
The moment of inertia of a body is a measure of its resistance to an increase in its rate of rotation. This is analogous to the mass of a body, which is a measure of its resistance to acceleration (by Newton's Second Law, a = F/m).

Parallel Axis Theorem

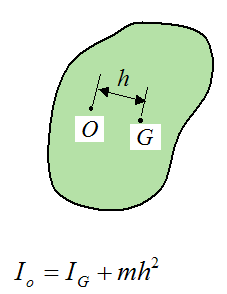
Using the parallel axis theorem we can calculate the moment of inertia of the body about a different axis passing through point O (call this I_o), based on the quantity I_G, the offset distance h, and the mass m of the body. Note that the axis passing through O must be parallel to the axis passing through G.





Moments Of Inertia Of Some Common Objects

Below are some common inertia values, all evaluated about an axis passing through the center of mass G, as shown. Note that m is the mass of the object.







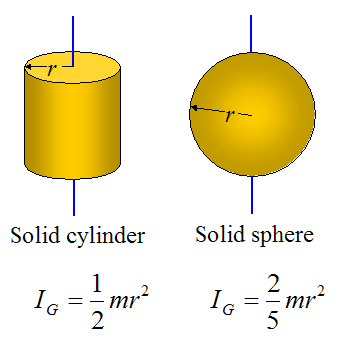
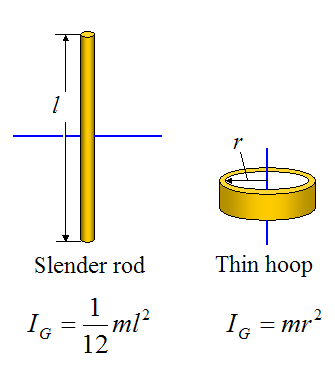
It's worth noting that, when calculating the moment of inertia in a plane, it is independent of the orientation of the xy axis in that plane. So, in the first figure, if the xy axis were turned at a different orientation (with origin still at G) the calculated moment of inertia would be the same.



Return to Useful Physics Formulas page


Return to Real World Physics Problems home page