About me and why I created this physics website.

Radius Of Gyration

Sometimes the moment of inertia of a body about a specified axis will be given using the radius of gyration, k. Given the value k and the mass of the body (m) we can calculate its moment of inertia (I), using the following formula:

Formula for moment of inertia using the radius of gyration

Consequently, the radius of gyration is given by

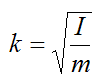
Formula for radius of gyration given I and m

The physical interpretation of the radius of gyration is that it is the radius of a uniform thin hoop (or ring), having the same moment of inertia (about an axis passing through its geometric center – shown below), as the given body about the specified axis.

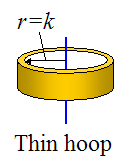
Thin hoop illustrating the radius of gyration


The moment of inertia of the thin hoop about the blue axis passing through its geometric center is:

Formula for moment of inertia using the radius of gyration and radius of thin hoop

The radius of gyration can be useful for listing in a table. If you want to know the moment of inertia of a complex shaped body about a given axis you simply look up its radius of gyration, and then (knowing its mass) apply the above formula to find the moment of inertia.



Return to Dynamics page


Return to Real World Physics Problems home page