About me and why I created this physics website.
The Physics Of Soccer
Source: http://en.wikipedia.org/wiki/Association_football. Author: http://en.wikipedia.org/wiki/User:Rdikeman
The Physics Of Soccer – The Magnus Effect
When a soccer player kicks a ball off-center it causes the ball to spin. The direction and speed of the spin will determine how much the ball curves during flight. It's the same principle as a curve ball in baseball. When throwing the ball, the pitcher imparts a fast spin which causes the ball to curve during flight.
The curve of the ball during flight is known as the Magnus effect. See the figure below.
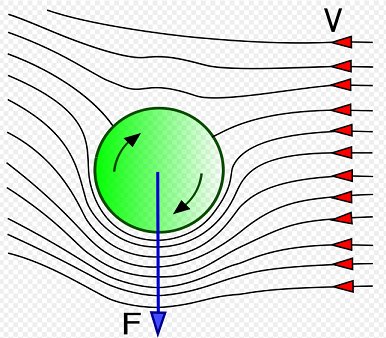
Source: http://en.wikipedia.org/wiki/Magnus_effect. Author: http://en.wikipedia.org/wiki/User:Gang65
As the ball spins, friction between the ball and air causes the air to react to the direction of spin of the ball.
As the ball undergoes top-spin (shown as clockwise rotation in the figure), it causes the velocity of the air around the top half of the ball to become less than the air velocity around the bottom half of the ball. This is because the tangential velocity of the ball in the top half acts in the opposite direction to the airflow, and the tangential velocity of the ball in the bottom half acts in the same direction as the airflow. In the figure shown, the airflow is in the leftward direction, relative to the ball.
Since the (resultant) air speed around the top half of the ball is less than the air speed around the bottom half of the ball, the pressure is greater on the top of the ball. This causes a net downward force (F) to act on the ball. This is due to Bernoulli's principle which states that when air velocity decreases, air pressure increases (and vice-versa).
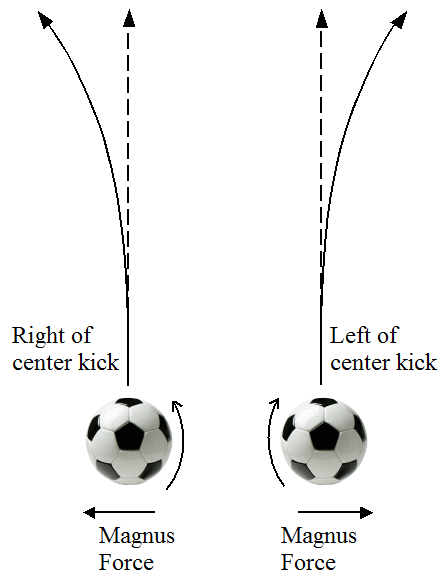
Therefore, when a soccer player kicks the ball right of center the ball spins counter-clockwise and the Magnus force acts left, causing the ball to curve left. When the ball is kicked left of center the ball spins clockwise and the Magnus force acts right, causing the ball to curve right. This can result in a ball deviating as much as several feet from the original trajectory by the time it reaches the net. This is no doubt a useful strategy when attempting to make a goal, since it makes the path of the ball less predictable to the goalie as he's preparing to block the shot.
Check out this great video showing the Magnus effect:
The Physics Of Soccer – Kicking
Kicking is fundamental to soccer. It is informative to analyze a soccer kick using physics. The schematic below illustrates a kick in action.
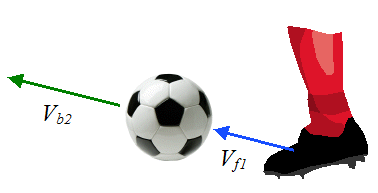
To analyze the kick we can treat it as an inelastic collision in one dimension, between soccer ball and foot. For inelastic collisions there exists an equation which accounts for the inelastic nature of the collision. This equation relates the initial and final velocities of the colliding bodies. The equation is:
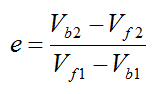
Where:
e is the coefficient of restitution. For all collisions this value is between 0 and 1. For e = 1 the collision is elastic and kinetic energy is conserved (the most efficient case). For e = 0 the collision is plastic (the most inefficient case), and the colliding bodies stick together and move with the same velocity, after impact
Vb1 is the velocity of the soccer ball before the kick
Vf1 is the velocity of the foot before the kick
Vb2 is the velocity of the soccer ball after the kick
Vf2 is the velocity of the foot after the kick
Next we have conservation of linear momentum for a one-dimensional collision:
Where:
mb is the mass of the soccer ball
mf is the effective mass for the foot
Note that "effective mass" refers to the stand-alone mass that would produce the equivalent dynamic effect upon colliding with the soccer ball. In reality, the player's foot is acted upon by external forces; forces which are generated by the player's leg muscles during the kick. Now, there exists an equivalent mass in place of the foot, which is not acted upon by external forces, and which (upon colliding with the ball), produces the same dynamic effect. This is called the effective mass for the foot. This effective mass is larger than the actual mass of the foot. For example, a 1 kg human foot striking a ball at 20 m/s (acted upon by leg muscle force), produces, say, the same dynamic effect as a stand-alone mass of 2 kg (not acted upon by any force), striking the ball at 20 m/s. It is necessary to think of a stand-alone mass in this way because the above equation has mass in it. If we were to use only the actual mass of the foot we would have to also include the forces acting on the foot. This would greatly complicate things. So to simplify the problem we use instead an effective mass for the foot in order to conveniently apply the above two equations. This allows us to obtain a reasonable solution without too much effort.
Now, combine the above two equations to obtain an expression for Vb2.
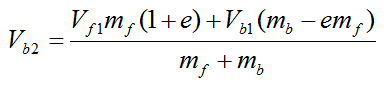
Since the ball is initially stationary, Vb1 = 0.
From reference [1] the effective mass for the foot is approximately four times that of the ball (mf = 4mb). Hence, the above equation simplifies to:
For professional players, the ball velocity (Vb2) can be as high as 60-70 mph. Soccer players want e to be as high as possible since this results in a more efficient kick with higher ball speed. This in turn depends on the kicking technique, among other things.
From the above equations we can determine the velocity of the foot after the collision:
This result makes sense since we expect the velocity of the foot to decrease somewhat after the kick.
Based on experimental results, the value of e for soccer kicks is between 0.46-0.68 [2, 3]. For FIFA approved soccer balls, the coefficient of restitution must be between 0.82-0.88 at 20 degrees Celsius and between 0.79-0.88 at 5 degrees Celsius. The coefficient is measured by dropping the ball onto a rigid surface from a height of 2 m and measuring the rebound height. The coefficient is given as the square root of the ratio of the rebound height to the initial drop height [4].
The coefficient of restitution depends on the mechanical properties of the ball, the ball temperature, the shoe, the ankle, and the foot during impact.
To gain an idea of the kick force generated by a professional soccer player during a kick we can use the impulse equation: FavgΔt = mbΔVb, where Favg is the average kick force during the impact between ball and foot, Δt is the time duration of the impact, and ΔVb is the change in velocity of the ball during impact. ΔVb = Vb2. If we use a time duration of Δt = 0.01 s, a ball mass of mb = 0.45 kg, and Vb2 = 30 m/s, we can calculate Favg. We get Favg = 1350 N.
References
1. A. Lees and L. Nolan, The biomechanics of soccer: a review, J. Sports Sci., 16, 211–234, 1998.
2. T. Bull-Andersen, H. Dorge, and F. Thomsen, Collisions in Soccer Kicking, Sports Eng., 2: 121-125, 1999.
3. H. Dorge, T. Bull-Andersen, H. Sorensen, and E. Simonsen, Biomechanical differences in soccer kicking with the preferred and the non-preferred leg, J. Sports Sci., 20: 293-299, 2002.
4. N. Wiart, J. Kelley, D. James, and T. Allen, Effect of temperature on the dynamic properties of soccer balls, Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology, vol. 225 no. 4 189-198, December 2011.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page