The Physics Of Skiing
An understanding of the physics of skiing is useful to skiers of all skill levels because it allows them to identify those key physics principles enabling them to properly execute certain moves, which is useful from a performance point of view. In addition to having an intuitive understanding gained from practice, understanding some of the physics theory behind skiing can help make sense of the mechanics involved, which is particularly useful for those who are just starting out.
The skiing physics behind different types of skiing will be discussed.
Physics Of Skiing – Downhill Skiing
Downhill skiing is also called alpine skiing. It involves high speed and quick turns down a sloped terrain. The skier gains speed by converting gravitational potential energy into kinetic energy of motion. So the more a skier descends down a hill, the faster he goes. The picture below shows a downhill skier.

Source: http://www.flickr.com/photos/alindquist_/3529374910
In competitive downhill skiing the goal is to cross the finish line the fastest, while navigating tight turns and obstacles throughout the course. An analysis of the physics is very useful in understanding how this is done. A skier maximizes his speed by minimizing resistance to motion, both from air resistance and snow resistance. A skier minimizes his air resistance (drag) by reducing his projected frontal area. He does this by going into a crouch position, which (along with improving his ability to hold balance) results in a lower drag force, which acts in a direction opposite his velocity, slowing him down. The picture below shows a downhill skier in a crouch position.

Source: http://www.flickr.com/photos/jonwick/4369246897
The equation for drag force (FD) is given by
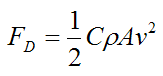
Where:
C is the drag coefficient, which can vary along with the speed of the skier. But typical values range from 0.4 to 1.0
ρ is the density of the air
A is the projected frontal area of the skier perpendicular to the flow direction (that is, perpendicular to his velocity v)
v is the velocity of the skier relative to the air
Minimizing drag force is an important consideration in the physics of skiing, especially for competitive racing. Body posture and the choice of race suit are two critical areas of focus in the effort to minimize drag.
The mass of the skier can also help counteract the drag force FD. A greater mass means a greater force of gravity acting on the skier, which means that the relative magnitude of FD becomes smaller. As a result, the skier reaches a greater velocity v.
In reality though, a heavier skier will generally be "bigger", meaning his projected frontal area will be greater, which may negate some of the gain achieved by being heavier. The net effect, however, is that a heavier skier usually goes faster. But this may compromise the ability of the skier to quickly go around turns, due to his greater bulk.
As mentioned, snow resistance is the other factor directly affecting speed. Just like for air resistance, we wish to minimize snow resistance in order to maximize speed. However, the techniques used for minimizing snow resistance are subtle, especially when the skier makes a turn.
Amateur (less experienced) skiers typically skid around their turns. This occurs when the skis are tilted on their edge and the exposed base of the skis "plow" into the snow head on. Although the skidding can be controlled and the turn successfully executed, it ultimately results in a significant loss in speed. This occurs because the "plowing" action generates frictional resistance with the snow, by physically pushing it. This frictional resistance is significantly more than the resistance seen if the skis were to glide on the snow, either with the base of the skis flat on the snow (while moving in a straight line in the direction of the skis), or with the edge of the skis planted into the snow (while carving around a turn, to be discussed in the next section). In both these cases, the skis are pointed in the same direction as their velocity (which is the same as the velocity of the skier). This is a necessary requirement for minimizing snow resistance.
The figure below illustrates a turn that is executed while skidding.
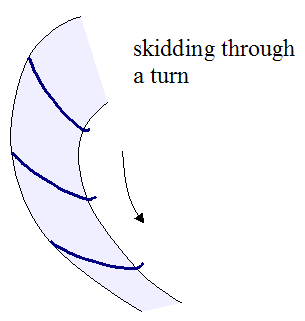
The path "swept" by the skis is the result of plowing the base of the skis through the snow. This happens when the skier turns his skis too sharply into the turn. This results in the momentum of the skier not changing direction quickly enough to match the direction the skis are pointed.
However, in some cases, a degree of skidding is unavoidable, but the key is to minimize it in order to minimize the speed reduction during the turn.
The most efficient turn occurs when the skier does a purely carved turn, in which the ski is pointing in the same direction as its velocity. The figure below illustrates this.

As shown in the figure above, in a purely carved turn there is no skidding, and the only snow resistance present is the very small sliding friction between ski and snow. As a result of this minimal level of friction between ski and snow, the speed reduction of the skier is minimized, and he is able to navigate the course faster. Carving turns is one of the more interesting areas of study in the physics of skiing.
It takes quite a bit of skill to execute a carved turn. World Cup level skiers are typically the only ones who are able to do it consistently.
The physics of carved turns will be described next.
Carved Turns
Ski shape is an important factor. Skis are often manufactured with a sidecut on both sides. The amount of sidecut determines the curvature of the ski, which is of a certain constant radius along the sidecut edge. The figure below illustrates a sidecut ski, where RSC is the sidecut radius.
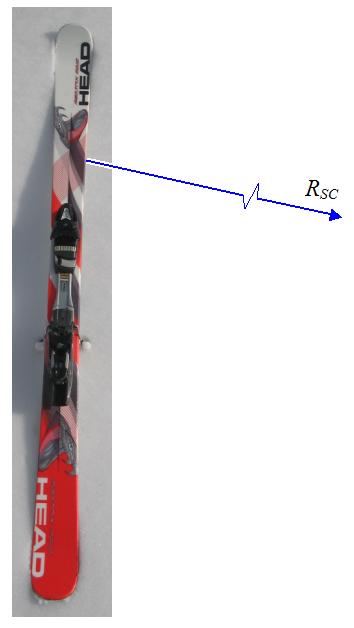
Source: http://en.wikipedia.org/wiki/Ski. Author: http://commons.wikimedia.org/wiki/User:Dbenbenn
The sidecut helps skiers make purely carved turns. It affects the physics by influencing the radius of purely carved turns, as will be discussed.
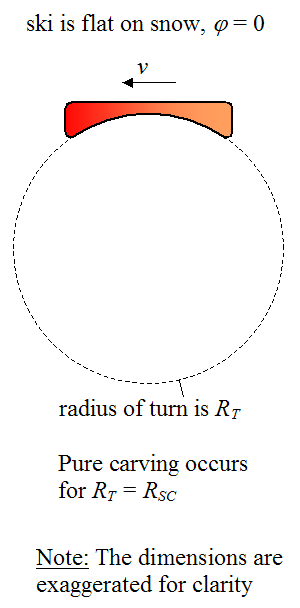
A purely carved turn can be done with a ski that is flat on the snow or tilted at an angle to the snow. The figure below illustrates a ski that is tilted at an angle φ to the snow. When the ski is flat on the snow φ = 0.
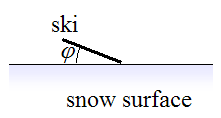
(Note: In reality the ski edge is pressed into the snow, for a given angle φ. This is discussed in more detail in the section on how to prevent ski slippage).
When the ski is flat on the snow, a purely carved turn is executed when the radius of the turn RT equals the sidecut radius RSC. This allows the ski to go around the turn without any skidding, since the ski is always pointed in the same direction as its velocity v. The figure below illustrates a purely carved turn for a ski that is flat on the snow.
When the ski is not flat on the snow, and φ does not equal zero, a purely carved turn can be executed by using the right amount of reverse camber on the ski. Reverse camber occurs when the force of the skiers foot on the ski causes the ski to bend in a shallow "U" shape, as shown below.

Skis can be manufactured with a camber which is opposite to that shown in the figure above. In other words, the ends of the ski touch the ground while the middle of the ski is elevated. This is done to control how much the ski flattens out when the weight of the skier is applied to the ski. A flat ski distributes the weight of the skier more evenly over the snow surface, which means the ski doesn't dig into the snow as much, and snow resistance is reduced. This is useful when skiing with no tilt on the skis. Alternatively, if the skis are manufactured flat, then the middle of the ski would sink more than the ends when the skier's weight is applied, and movement through the snow would be more difficult. However, the amount that the middle of the ski bends when a given weight is applied depends on the stiffness of the ski, which can vary in different skis.
There are times when reverse camber is desirable, such as when carving a turn, where the ski is tilted at a certain angle φ to the snow (which will be explained next). This allows the ski to match the radius of the turn. This tells us that skis must largely be selected based on the skier's weight, and how much reverse camber is desired, which depends on the type of skiing to be done.
To understand why a reverse camber is necessary when making a purely carved turn at some tilt angle φ, let's first look at the case where the ski is tilted, but with no reverse camber. The figure below illustrates this.
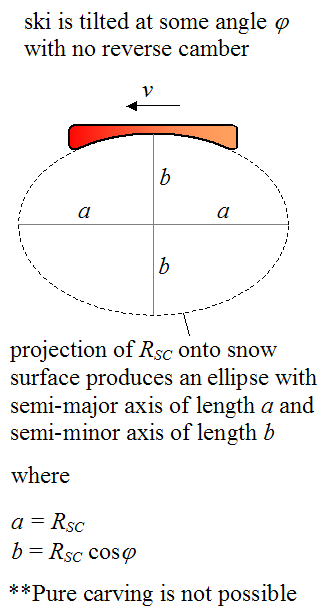
The projection of the sidecut radius RSC onto the snow surface must be a circle in order for the inside edge of the (tilted) ski to make a purely carved turn. But since the projection of the sidecut radius onto the snow surface is an ellipse, a purely carved turn is not possible. In other words, the inside edge of the ski would not be able to follow the curve defined by the ellipse. There would be some skidding as a result of the ski pointing in a direction different from the direction of its velocity v.
Therefore, the ski needs to have a reverse camber such that the sidecut radius, when projected onto the snow surface, is a circle. The reverse camber must be great enough to shorten the length of the semi-major axis so that it equals the length of the semi-minor axis, which gives us a circle (or very close to it). This allows the inside edge of the ski to make a purely carved turn. The figure below illustrates this.
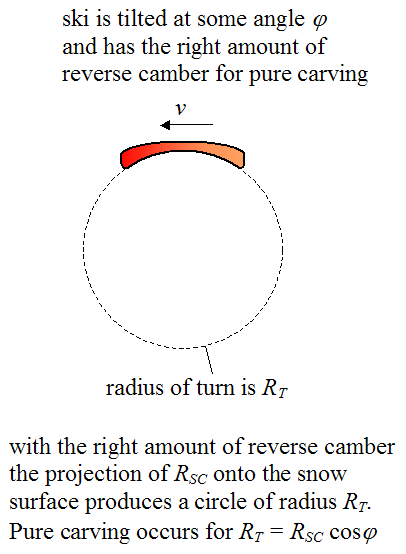
The right amount of reverse camber reduces the length of the semi-major axis (in the previous figure) so that its length equals the length of the semi-minor axis (length b = RSC cosφ). As a result, the projection of RSC onto the snow surface produces a circle of radius RSC cosφ. This is the radius of the turn for pure carving to occur. This equation tells us that the greater the tilt angle φ, for a given RSC, the smaller the corresponding carving radius RT, and the greater the reverse camber necessary to achieve it.
In the next section we will take a closer look at carving and how it relates to sidecut edge penetration into the snow.
Closer Look At Carving And Sidecut Edge Penetration
For a given tilt angle φ and sidecut radius RSC, the maximum amount of reverse camber occurs when the sidecut edge presses into the snow. To understand this consider the following. When a straight ski (with no camber) is edged into the snow at an angle φ, only the tip and tail part of the ski are touching the snow, and there is a gap in the middle of the ski between the sidecut edge and the snow surface. This gap is greater for a smaller sidecut radius, and this gap is smaller for a larger sidecut radius. The maximum amount of reverse camber occurs when this gap is closed – in other words, when the sidecut edge presses into the snow. So the larger the gap, the more reverse camber is possible, since the ski can bend more in the middle before the sidecut edge presses into the snow.
A ski with a smaller sidecut radius (and larger gap between sidecut edge and snow surface), can accommodate a greater amount of reverse camber, which means it can carve smaller radius turns. A ski with a larger sidecut radius (and smaller gap between sidecut edge and snow surface), can accommodate a lesser amount of reverse camber, which means it is best suited for carving larger radius turns.
Therefore in summary, skis with a larger sidecut radius RSC are best suited for carved turns with a small tilt angle φ (since they can only accommodate a lesser degree of reverse camber). And skis with a smaller sidecut radius RSC work well for larger tilt angles φ (since they can accommodate a greater degree of reverse camber). This tells us that carved turns of small radius RT are best executed with skis that have a smaller RSC, since the corresponding tilt angle φ can be high. But carved turns of large radius RT are best executed with skis that have a larger RSC, since the corresponding tilt angle φ can only be low.
Given the complexity of all these inter-related factors, the ability of a skier to make a purely carved turn comes down to his ability to recognize the terrain and make adjustments, based on the factors just mentioned. Clearly, carving adds substantial complexity to the physics involved.
In the next section we will look at skidding in more detail.
Skidding
The physics of skidding is different from the physics of carving. Unlike carving where a skier eases into the turn, a skidded turn is initiated by the skier simultaneously tilting the edge of the skis into the snow and pivoting his skis in the direction he wants to turn. This results in the skier turning in that direction, due to the plowing effect of the skis with the snow. The illustration below shows the beginning of a turn, in which the skis are initially pointed in a certain direction, at a certain steering angle.
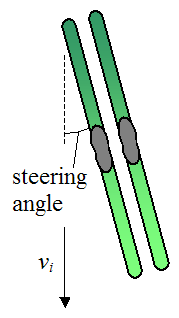
where vi is the initial velocity of the skier.
Since the skis are pointed in a direction that is different from the initial velocity vi, it is unavoidable that skidding will occur. The steering angle determines how much the skier turns, and how much he slows down. A steering angle of zero results in the skier moving in a straight line with no turning and no slowing down. A steering angle of 90° results in the skier slowing down with no turning, since the force of the snow plowing into his skis is head-on with no sideways component to turn him. Therefore, for turning purposes the optimal steering angle is somewhere in between zero and 90° – usually 45° or more for many skiers.
When a skier skids around a turn, a reverse camber in the skies causes the skis to self-steer. Due to the curvature of the skis, the snow impacts the skis at different angles along its length. This causes the skis to self steer.
To understand the physics behind this self-steering phenomenon, consider an exaggerated representation of a ski shown below. In this illustration the reverse camber of the ski is represented by two flat edges, in which the leading (front) end of the ski is at a greater angle to the snow than the tailing (back) end of the ski. Since the leading end of the ski is at a greater angle to the snow than the tailing end, the snow impacts it more head-on, and with greater force. As a result, a net counterclockwise torque is generated, which causes the skis to self-steer.
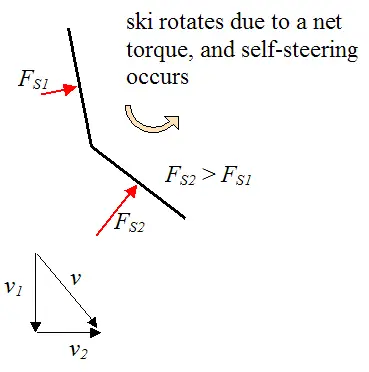
Where:
FS1 is the resultant force of the impacting snow acting on the tail end of the ski
FS2 is the resultant force of the impacting snow acting on the leading end of the ski
v1 is the velocity component of the skis along the original direction of motion
v2 is the velocity component of the skis in the sideways direction, in the direction of the turn
v is the resultant velocity of v1 and v2
Since skidding is a form of snow resistance (as described previously) which acts to slow the skier down, then v < vi. Note that this neglects any possible change in speed due to a change in the gravitational potential energy of the skier. But regardless, snow resistance results in a lower speed v than would occur if there were no skidding when going around the turn.
A skier can enhance the self-steering affect by leaning forward on his skis, and shifting his weight closer to the front of the skis. This results in the leading ends of the skis bending even more, which increases FS2 in the above figure. This in turn causes even more self-steering. The figure below illustrates this. The lightly colored line represents the ski before the skier shifts his weight closer to the front.
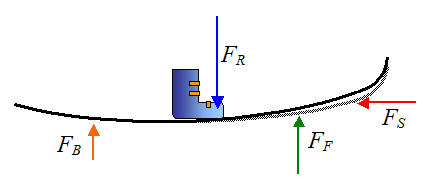
Where:
FB is the resultant force of snow acting on the tail (back) end of the ski
FF is the resultant force of snow acting on the leading (front) end of the ski
FR is the resultant force exerted by the skier's foot on the top of the ski
FS is the resultant force of the impacting snow acting on the entire ski
Since FF > FB the leading end of the skis bend even more.
The skis are also able to self-steer due to the front of the skis being a bit wider than the back. This causes more snow to be plowed at the front (leading) end of the skis than the back, which results in a greater force being exerted by the snow in the front than the back. The result of this is a net torque that turns the skis in the same direction as the reverse camber effect does (discussed previously). This ski-width effect, however, is not as great as the reverse camber effect in its self-steering ability.
In the next section we will look at the forces acting on a skier that is going around a purely carved turn.
Force Balance For Skier Going Around A Purely Carved Turn
As explained in the previous section, making a purely carved turn is desirable for a skier since it minimizes how much he slows down. Thus, it is useful to analyze the forces acting on a skier during such a turn.
To begin the analysis, we must first define the orientation of the skier on the ski slope. This is necessary because the force of gravity affecting the motion of the skier changes depending on which direction he is skiing along the slope. The figure below shows a schematic defining the orientation of the skier on the slope.

Where:
g is the acceleration due to gravity, which is 9.8 m/s2 on earth
α is the slope angle. This angle is zero for a flat horizontal surface
β is the angle the skis make with the equipotential line along the surface of the slope. The equipotential line is the line of constant altitude, and is perpendicular to the direction of gravity
RT is the radius of the turn
v is the velocity of the skier along the turn, pointing in the direction of the skis
The coordinate system xy is oriented such that the y-axis is perpendicular to the surface of the slope, and the x-axis lies along the surface of the slope and is perpendicular to the velocity v of the skier, at the instant shown.
(Note, we are assuming that the surface of the ski slope is planar and that three-dimensional effects are negligible).
Next, set up the free body diagram of the skier, as shown in the schematic below.
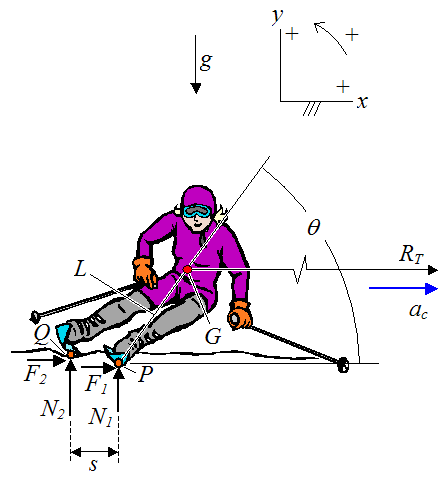
Where:
θ is the angle between the slope (in the x-direction) and the line passing through points P and G. This is defined here as the angle of "lean" of the skier
G is the center of mass of the system (which consists of skier plus skis, which together can be treated as a rigid body)
P is the approximate contact point between the inside ski and the snow
Q is the approximate contact point between the outside ski and the snow
L is the distance between point P and point G
ac is the centripetal acceleration of point G. This acceleration is in the x-direction and points towards the center of the turn, at a given instant
F1 is the contact force in the x-direction, with the snow, acting on the ski at point P
N1 is the contact force in the y-direction, with the snow, acting on the ski at point P
F2 is the contact force in the x-direction, with the snow, acting on the ski at point Q
N2 is the contact force in the y-direction, with the snow, acting on the ski at point Q
s is the distance along the x-direction, between points P and Q
Note that v is the instantaneous velocity of the center of mass G. This velocity is pointing out of the page in the above figure.
The center of mass G has zero acceleration in the y-direction. Therefore, the forces in the y-direction acting on the system must sum to zero. Mathematically this can be written as
where m is the mass of the system (which consists of skier plus skis).
Apply Newton's second law in the x-direction:
The centripetal acceleration is given by
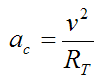
This equation is substituted into equation (2).
We can approximate the system as being in rotational equilibrium, which means there is zero moment acting on the system about the center of mass G, about an axis pointing out of the page. Mathematically we can write this as
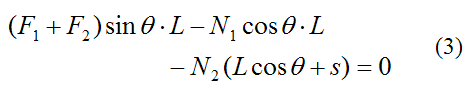
Equations (1)-(3) can be solved for any three unknown quantities. There is no closed form solution for these equations, so they must be solved numerically.
To illustrate the use of these equations let's do a sample calculation. For example, let's say at a given instant α = 20°, β = 60°, L = 1.1 m, s = 0.40 m, v = 5 m/s, the sidecut radius RSC = 14.8 m, the angle of tilt φ = 30°, and N1 = F1 = 0 (meaning all the push force is on the outside ski). What is the angle of lean θ?
The mass m of the skier does not need to be known since it cancels out of the equations. From before, the radius RT is given by RT = RSC cosφ = 14.8×cos(30) = 12.82 m. Thus, solving (1)-(3) numerically we get the angle of lean as θ = 88.3° .
When skiing on a slope, the radius of the turn RT (whether carved or skidded) is not constant throughout the turn, and some variation is normal, especially since the force of gravity relative to the skier (along his trajectory) changes along with his changing angle β on the slope, as shown in equation (2). This naturally changes the angle of lean θ, which tends to change the tilt angle φ the skier makes with the snow. Consequently, this changes the radius of the turn RT. This complicates the physics analysis.
As a final check in the above solution, we must look at the angle of the force applied to the ski to ensure that it does not slip on the snow. But before doing that we must first acquire some background understanding, which will be given in the next section.
Preventing Ski From Slipping On Snow
There are two cases to consider with regards to ski slippage and how to prevent it. The first case is when a ski is on a horizontal and flat snow surface. To avoid slipping, the force applied to the ski by the skier's foot must be perpendicular (at 90°) to the plane of the ski in contact with the snow. This is because the friction between the ski and the snow is very small so any sideways force can cause the ski to move (slip).
The second case is when a ski is on a sloped snow surface. To avoid slipping, the ski must be pressed into the snow at a certain tilt angle, such that the component of the applied force, parallel to the plane of the ski, points into the snow. The schematic below illustrates this.

Where:
φ is the angle of tilt between ski and snow, as shown
δ is the angle between the applied force and the snow surface, as shown
ψ is the angle between the applied force and the ski, as shown
FR is the resultant force exerted by the skier's foot on the top of the ski
To prevent slipping, the angle ψ must be greater than or equal to 90° . This means that the component of FR parallel to the plane of the ski, will either be zero (for ψ = 90°), or it will point directly into the snow, towards the right (for ψ > 90°), and the "wall" of snow will prevent it from slipping.
However, if the angle ψ is less than 90°, then the component of FR parallel to the plane of the ski, will point outward (towards the left), and the ski will slip outward (out of the "trench"). Note that we are ignoring the relatively small weight of the ski which would result in the critical angle being slightly different from 90° .
By geometry, this means that for no slipping, δ must be greater than or equal to 90−φ.
We can now check the sample calculation in the previous section to see if the ski slips on the snow.
We must check the angle of the applied force FR acting on the outside ski (exerted by the skier's foot). Ignoring the relatively small mass of the ski, this force is equal and opposite to the force exerted on the ski due to F2 and N2. Therefore, from geometry, the angle δ = atan(N2/F2). Substituting the quantities given in the problem statement, we get δ = 68.5°, which is greater than 90−φ = 60° . Therefore, the ski does not slip.
In the next section we will take a closer look at slipping, and how it can be prevented based on whether the skier is on hard snow or soft snow.
A Closer Look At Slipping
An important first requirement for no slipping to occur on a slope, is that the ski edge must be able to penetrate the snow (as described previously). The ability of a ski edge to be pressed into and penetrate the snow depends on the hardness of the snow. For example, it is common for a World Cup racer to apply all his (effective) weight FR on his outside ski, when going around a turn on hard snow. This is because a high force is needed to penetrate the hard snow surface and gain traction. If the (effective) weight of the skier were distributed on both skis then slipping might occur, since neither ski may be pushing on the snow surface hard enough to penetrate it. On softer snow, however, it is common to distribute the weight more evenly on both skis when going around a turn (since it is easier to penetrate the snow).
In the next section we will look at the basic mechanics of nordic (cross-country) skiing.
Nordic Skiing

Source: http://en.wikipedia.org/wiki/Skiing. Author: http://commons.wikimedia.org/wiki/User:Che
Unlike downhill skiing, nordic skiing takes place on flat terrain, with an occasional slope or hill. This means that a nordic skier must push himself along using his own power, unlike a downhill skier who gains speed by way of converting gravitational potential energy into kinetic energy of motion. Thus, the physics of nordic skiing is very different from the physics of downhill skiing.
A nordic skier pushes himself along on the snow surface using his skis, and to a lesser extent his poles. The skier pushes himself off the snow surface with his skis by pushing on the snow in a direction perpendicular to the ski. Since there is almost no friction between the ski and the snow, the only way to push off the snow is by pressing the edge of the ski into it and pushing off in a direction perpendicular to the ski. This is basically the same principle as a skater uses to push off the ice with his skate blades. Thus, the physics of nordic skiing is similar to the physics of skating. The figure below illustrates the principle a nordic skier uses to push off the snow.
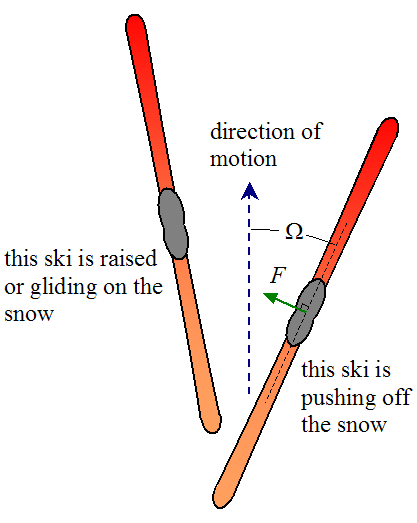
Where:
F is the perpendicular force exerted on the ski by the snow
Ω is the angle between the direction of motion and the pushing ski, as shown
As the skier pushes off with his rear leg, a perpendicular force F is exerted on the ski by the snow. The component of the force F that points forward (in the direction of motion) is what pushes the skier forward. At the same time, his other ski is either raised or gliding on the snow. As the skier moves forward he then switches to the other leg and pushes off the snow with that one, and the process is mirrored. To push off the snow with greater forward force (and accelerate faster), the skier increases the angle Ω, which increases the component of force in the direction of motion.
To slow down, the skier can use a "snowplow" in which he forms a V-shape with the front of his skis, which results in a component of the force F acting opposite his direction of motion, but on both skis, instead of one. This slows him down, eventually stopping him. The figure below shows a picture of a recreational skier using the snowplow principle to slow down.

Source: http://www.flickr.com/photos/thomasrdororg/1217019265
In the next section we will look at ski jumping.
Ski Jumping

Source: http://www.flickr.com/photos/tigerzeye/243447095
In the sport of ski jumping the goal is to jump the farthest down an inclined slope. This is accomplished in basically two ways. The first way is by gaining as much speed as possible upon takeoff from the ramp. This is done by minimizing the air resistance (drag) on the skier's body as he descends down the hill. The skier minimizes drag by going into a crouch position. The crouch position in turn reduces the projected frontal area of the skier, which reduces drag according to the following equation (described in the first section):
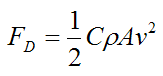
Where:
FD is the drag force acting opposite the direction of motion of the skier
C is the drag coefficient, which can vary along with the speed of the skier. But typical values range from 0.4 to 1.0
ρ is the density of the air
A is the projected frontal area of the skier perpendicular to the flow direction (that is, perpendicular to his velocity v)
v is the velocity of the skier relative to the air
The second way to maximize jump distance is after takeoff, while the ski jumper is airborne. In this stage, the skier must orient his body and skis so as to minimize drag and maximize lift. He does this by leaning forward while making a V-shape with his skis. Spreading the skis into a V-shape increases the projected frontal area of the skis (perpendicular to the direction of air flow relative to the skier). This increases the lift force generated by the air rushing past the skier. This lift force in turn slows down his rate of descent so that he stays airborne longer before landing, thus increasing his distance down the slope. The lift force generated by the skier is similar to how an airplane wing generates lift.
The picture below shows a ski jumper making a V-shape with his skis.

Source: http://www.flickr.com/photos/maxf/4448268042
The physics of ski jumping is a very complicated subject. A reasonably accurate analysis of it requires computational fluid dynamics and wind tunnel testing.
The landing hill of the ski jump curves downward in a shape similar to the trajectory of the ski jumper, as he falls. This enables the ski jumper to land with minimal impact force on the hill. This is because his normal velocity component relative to the hill, just before he lands, is minimal.
In the next section we will look at freestyle skiing.
Freestyle Skiing
In the freestyle skiing known as aerial freestyle, a skier performs aerial acrobatics, spinning and twisting in the air. The basic physics principle at work here is the conservation of angular momentum. The angular momentum of the skier is determined at takeoff (from a ramp), and cannot be changed once the skier is airborne. So to make turns in the air the skier must give himself initial rotation upon takeoff. Once airborne, the skier can alter his body shape in order to produce an impressive aerial display of tricks and twists for the crowd, during which his angular momentum remains constant. The picture below shows an aerial freestyle skier performing an acrobatic trick.

Source: http://www.flickr.com/photos/bjacksonphotography/4230404806
Another type of freestyle skiing is mogul skiing, in which a skier skis over a terrain covered with many bumps. To minimize the jarring forces acting on him, a mogul skier rides the bumps using mostly up and down leg movement, like a shock absorber, while minimizing the movement of his upper body. This keeps his center of mass moving in as straight a line as possible. And by Newton's Second Law, this keeps the forces acting on him as low as possible.
Thus, the physics behind mogul skiing involves keeping the acceleration of the center of mass of the skier minimal to avoid excessive jarring. And this is accomplished by making the center of mass of the skier move in as straight a line as possible.
The ability of skis to adapt to a terrain (either for moguls or other types of skiing), is a function of their torsional stiffness and flexural stiffness. Torsional stiffness is the ability of the ski to resist twisting along its length. This is related to the ability of the ski to maintain "biting" contact with the snow. Flexural stiffness is the ability of the ski to resist bending (such as reverse camber). For riding on harder, or icier snow, a ski with a greater flexural stiffness is generally desired since it can ride the bumps and undulations better. For softer snow, a less flexurally stiff ski is usually desired. Clearly, ski stiffness and adaptability to the terrain is an important consideration in the physics of skiing.
In the last section we will look at basic ski maintenance required for optimal performance.
Ski Maintenance
Good ski maintenance also ties into the physics of skiing by optimizing the performance of the ski on the snow, as explained in the points below:
• Waxing the bottom of skis protects them from wear and water penetration, the latter of which can damage the skis. Wax also makes the bottom of the skis waterproof, reducing wet-drag (suction) friction, which is caused when excess water collects at the bottom of the skis.
• The edges of the skis must be kept sharp using a stone grinder, much like skate blades, to allow for easier turning and stopping.
Return to The Physics Of Sports page
Return to Real World Physics Problems home page
Free Newsletter
Subscribe to my free newsletter below. In it I explore physics ideas that seem like science fiction but could become reality in the distant future. I develop these ideas with the help of AI. I will send it out a few times a month.